Презентация на тему Циклы по условию на языке Pascal

с постусловием  Repeat… until  на примере решения задач с использованием рекуррентных

соотношений и бесконечных рядов.

Цикл – процесс многократного повторения каких-либо действий. 
Язык Паскаль имеет три оператора, с помощью которых можно организовать циклическую структуру:
Цикл с параметром (счетчиком) “Для” (For ... )
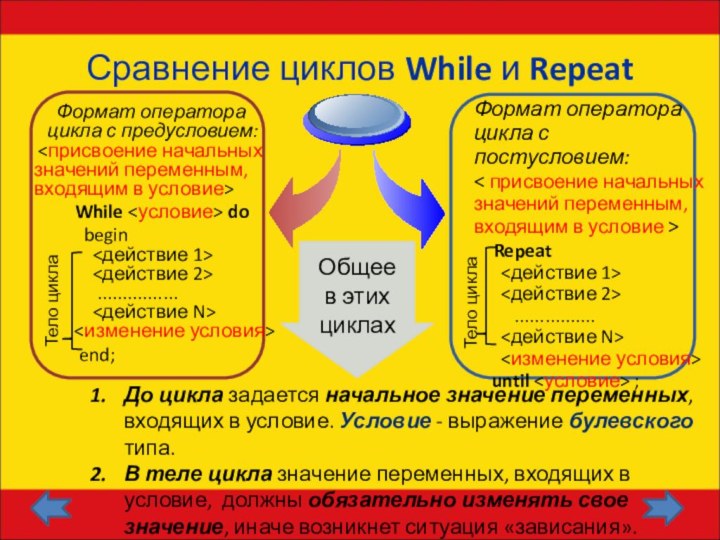
Цикл с предусловием “Пока” (While ... do)
Цикл с постусловием “До” (Repeat ... until)

Повторим!

to … do начальное значение переменной i меньше

предельного.
Шаг изменения i по умолчанию равен +1.
Переменная i НИКОГДА не может стоять СЛЕВА от оператора присваивания «:=».

var i: integer; {счетчик}
Begin
For i:=1 to 10 do
Writeln(i);
End.

Программа

Надо помнить

Тип переменной i – любой скалярный (integer, byte, char, др.) КРОМЕ вещественного.
i НИКОГДА не может быть real .

Пусть решается простая задача вывода на экран целых чисел от 1 до 10.
Для этой задачи идеально подходит цикл со счетчиком For…to… do .

заданным шагом;
для расчета с заданной точностью сумм бесконечных асимптотических

рядов, с помощью которых выражаются тригонометрические функции, трансцендентные числа π = 3,1415… и основание натурального логарифма e=2,72…;
для вычисления квадратного корня из числа методом Герона.

Когда For…to…do уступает место

Если число повторений известно наперед, цикл For идеален!

Циклы While… do и Repeat… until используются в целом классе задач, когда повторные вычисления заканчиваются по заданному наперед условию:

цикла с предусловием:

входящим в условие>
While <условие> do 
begin <действие 1>   <действие 2>      ................   <действие N>   <изменение условия>
end;

Формат оператора цикла с постусловием: < присвоение начальных значений переменным, входящим в условие >
Repeat    <действие 1>    <действие 2>   ................    <действие N> <изменение условия> until <условие> ;

До цикла задается начальное значение переменных, входящих в условие. Условие - выражение булевского типа.
В теле цикла значение переменных, входящих в условие, должны обязательно изменять свое значение, иначе возникнет ситуация «зависания».

Сравнение циклов While и Repeat

целых чисел на экран с использованием цикла While… do:

i:

=1; {начальное значение}

i:=i+1

Программа

var i: integer; {счетчик}
Begin

Блок-схема алгоритма

While i<=10 do
begin
Writeln(i);

end; {While}
End.

проверяется на входе в цикл, то при неверном условии

цикл не выполняется ни разу, т.е. не выполняются операторы, стоящие в теле цикла.

Операторы, входящие в тело цикла, обязательно заключаются в операторные скобки, если в теле цикла более одного оператора. В противном случае будет выполняться только первое действие, стоящее под заголовком цикла.

В теле цикла должно обязательно выполняться действие, приводящее к изменению условия, иначе цикл станет бесконечным. Оператор, в котором изменяются переменные, входящие в условие, может стоять не обязательно в конце цикла.

выводе 10 целых чисел на экран с использованием цикла Repeat…until:

i:

=1; {начальное значение}

i:=i+1

Программа

var i: integer; {счетчик}
Begin

Блок-схема алгоритма

Repeat
Writeln(i);

Until i>10
End.

из цикла, то цикл выполняется хотя бы один раз.

Все

операторы, стоящие в теле цикла, выполняются ДО проверки условия, поэтому операторные скобки не ставятся.

В теле цикла должно обязательно выполняться действие, приводящее к изменению условия, иначе цикл станет бесконечным. Оператор, в котором изменяются входящие в условие переменные, может стоять не обязательно в конце цикла.

N раз, суммируя результаты бросков. Напишите программу, определяющую победителя

после N бросков.

Какой цикл целесообразно использовать?
Почему?

Два игрока A и B бросают кубик и суммируют результаты бросков. Победителем объявляется игрок, набравший первым объявленную сумму очков S. Напишите программу, определяющую победителя.

Два варианта одной задачи:

Вариант 1

Вариант 2

на работу из дома (пункт А) в офис (пункт

B). Расстояние между домом и офисом равно 1 км. Пройдя половину пути, джентльмен вспомнил, что не попрощался с семьей, повернул назад и прошел третью часть расстояния и, боясь опоздать на работу, снова повернул и прошел четверть расстояния. Затем снова повернул и прошел 1/5 расстояния и т.д.

A

На каком расстоянии от офиса окажется джентльмен, если продолжит свои метания? Провести вычисления расстояния с точностью до 1 см.

1/2

-1/3

1/4

-1/5

1/6

и т.д.

(А), можно записать так: SА

= 1/2 - 1/3 + 1/4 - 1/5 + 1/6 – 1/7 +… (-1)i+1 /i… Так как расстояние АВ=1, джентльмен окажется от места работы на расстоянии S: S=1-SА = 1- [1/2 - 1/3 + 1/4 - 1/5 + 1/6 - 1/7 +… (-1)i+1 /i … Таким образом, решение задачи сводится к вычислению суммы гармонического ряда:  S= 1-1/2 + 1/3 – 1/4 + 1/5 -… (-1)i+1 /i -… 
Суммирование продолжаем, пока абсолютное значение разности сумм, вычисленных на (i+1)-м шаге и i-м шаге, больше наперед заданного малого числа eps , т.е. |S-S1|> eps.  Таким образом, ряд вычисляется приближенно с заданной погрешностью.
Для решения задачи используем цикл While.

harmony_riad; {Вычисление гармонического ряда};   uses crt;   const eps=0.00001; {заданная

точность вычисления}   var     i: integer; S,S1 : real; p: integer;
Begin   clrscr; {очистка экрана}   s1:=0; {начальное значение сумматора}   s:=1; {суммирование 1-го члена ряда}   i:=1; {начальное значение для 1-го члена ряда }   p:= -1; {знак числа отрицательный}   while abs(s1-s) > eps do     begin     s1:=s; {запоминаем сумму, вычисленную на предыдущем шаге}     i:=i+1; {формирование следующего члена ряда числа }     s:=s+p/i; {суммирование знакопеременного ряда}     p:= - p; {смена знака}     end; {while} 
  writeln('S от офиса=', s:7:5);   readln
End.

рекуррентной последовательности чисел (от латинского «recurrere» – «возвращаться»).
Это

понятие вводят так: пусть известно k чисел a1, … , ak , которые являются началом числовой последовательности. Следующие элементы этой последовательности вычисляются так: ak+1=F(a1, … , ak); ak+2=F(a1, … , ak+1); ak+3=F(a1, … , ak+2);…,
ak+i=F(a1, … , ak+i-1)
Величина k называется глубиной рекурсии.

метода рекуррентных соотношений вычисляют:
арифметические и геометрические последовательности;
последовательность

чисел Фибоначчи;
бесконечные последовательности (ряды) для тригонометрических функций;
бесконечные последовательности (ряды) для функций ex, sqrt(x), ln(1+x);
выражения вида:

целого числа а по рекуррентной формуле Герона Xi+1=(X i+ а/X

i)/2  при заданной точности вычисления eps.
Алгоритм вычисления. Зададим X1 - начальное значение корня из числа а.  Например, X1= a/2.  Тогда каждое следующее приближение вычисляется через предыдущее: Х2=(X1 + а/X1)/2 Х3=(X2 + а/X2)/2 ----------- Xi+1=(Xi + а/Xi)/2  Вычисление продолжаем до тех пор, пока выполнится модуль разницы между Xi+1и Xi станет меньше заданной погрешности вычисления eps: |Xi+1 - Xi|< eps Для решения задачи используем цикл Repeat… until.

по фоpмуле Герона} {х=(х+а/х)/2}   uses crt;   const eps=0.0001;   var 

    a: integer;     x, x1: real; Begin   clrscr;   write('Введите число а=');   readln(a);   x:=a/2; {начальное значение корня}   repeat     x1:=x; {запоминаем предыдущее приближение корня}     x:=(x+a/x)/2; {вычисляем (i+1)-е приближение корня}   until abs(x-x1)

ряда S=x – x3/3! + x5/5! - x7/7! +...

c заданной точностью eps.
Будем использовать рекуррентную формулу, с помощью которой каждый последующий член ряда выражается через предыдущий., т.е. справедливо соотношение:        un = q un-1
Определяем величину q, последовательно рассмотрев отношение второго члена к перовому, третьего ко второму, четвертого к третьему и т.д.:       q1= u2 / u1 = - (x3/3!)/x = - x2/(2 * 3)      q2= u3 / u2 = - (x5 / 5!) / (x3/3!) = - x2/(4 * 5)      q3= u4 / u3 = - (x7 / 7!)/ (x5/ 5!) = - x/(6 * 7)
Для произвольного q справедлива рекуррентная формула:      q = - x2 / k/(k+1), где k= 2, 4, 6, ...
В языках программирования стандартная функция sin(x) рассчитывается с помощью асимптотического ряда S.

real;  к : integer;
Begin
write

(‘Введите x='); readln(x);   s:=0; {обнуление суммы}   к:=0; {начальное значение переменной k}   u:=x; {первый член ряда}   while abs(u) > eps do     begin       s:=s+u; {суммируем ряд}       к:=к+2; { формируем четное число }        u:= - u * sqr(x) / к/ (к+1) ; {k-член ряда}     end;
writeln (' сумма ряда S=',S);
writeln (' sin x=', sin(x));   readln
End.

так:
a, a+d, a+2*d, a+3*d,…, a+(N-1)*d.

Здесь a – первый член последовательности, d – разность между двумя соседними членами, N – число членов последовательности.
Например:
1 + 3 + 5 + 7 + 9 + … + 99 (a=1, d=2)
2 + 4 + 6 + 8 +…+ 100 (a=2, d=2)

Два типа задач:
Вычислить сумму S при заданном числе членов N (используем цикл For).
Определить число членов N при достижении заданной суммы S (используем цикл While).

последовательность, в которой отношение между ее членом и членом,

ему предшествующим, есть величина постоянная.

В символьной записи это можно записать так:
a, a*r, a*r2, a*r3, … , a* r(N-1)
Здесь буквой a обозначен первый член последовательности, буквой r – ее знаменатель и буквой N – число членов последовательности.
Например, если a=4, r=0.5, N=7, получаем последовательность
4, 2, 1, 0.5, 0.25, 0.125, 0.625

В сундуке лежали изумруды. Пришел первый сын и взял

половину того, что было. Пришел второй сын и взял половину того, что осталось и т.д. Каждый из сыновей приходил и забирал половину того, что осталось. Наконец, пришел последний, седьмой сын и увидел почти пустой сундук — с двумя изумрудами.
Сколько изумрудов лежало в сундуке первоначально?
При решении задачи будем использовать цикл While…do.

Задача «Изумруды»

Блок-схема

Задача

i=7 'номер 7-го сына
q=2

'седьмому сыну досталось 2 изумруда
r=2 ‘разность геометрической прогрессии
WriteLn(‘i=‘, I, ‘ q=‘, q)
While i>1 do
begin
q=q*r ‘ вычисление i-того члена прогрессии
i=i-1 ' номер следующего сына уменьшается на 1
WriteLn(‘i=‘, I, ‘ q=‘, q)
end;
WriteLn(‘всего ‘,q,’ изумрудов’)
End.

вычислить с разной точностью eps>0:
Y1=ex = 1+x/1! + x2/2!

+…+ xn/n! …;
Y2= cos(x) = 1- x2/2! + x4/4! -…+ (-1)n x2n/(2n)! +…;
Y3= ln(1+x)= x – x2/2 + x3/3 -… + (-1)n-1 xn/(n)+…
2. Определить количество итераций (повторений) n в зависимости от eps.
3. Занести данные в таблицу:

знаменитых чисел в математике , вычисленных приближенно, является число

π.
Число π определяется как отношение длины окружности к ее диаметру.
Вот значение π до 16-го знака:
3.1415926535897932…
Числу воздвигают монументы и посвящают стихи.
Во всех алгоритмических языках есть стандартная функция для вычисления числа π. В языке Паскаль это функция Pi.

Гордый Рим трубил победу Над твердыней Сиракуз; Но трудами Архимеда Много больше я горжусь. Надо только постараться И запомнить все как есть: Три – четырнадцать – пятнадцать – Девяносто два и шесть! (С.Бобров )

очень интересная история. Еще в 200 г. до нашей

эры греческий математик Архимед (тот самый Архимед, который, купаясь в море, вдруг воскликнул «Эврика!» и открыл знаменитый закон Архимеда!) утверждал, что число π меньше, чем 22/7 и больше, чем 223/71.

Многие математики выводили формулы для приближенного
вычисления π в виде бесконечных рядов, например:
π = 4 – 4/3 +4/5 – 4/7 + 4/9 - 4/11 + …
(Готфрид Лейбниц ( около 1673 г.)
π = 2sqrt(3)[1 – 1/(3*3) +1/(32 *5) - 1/(33 *7)+…],
(Шарп ( около 1699 г.))
π = sqrt(6 + 6/12 + 6/22 + 6/32 + 6/42 + 6/52… )
(Эйлер ( около 1736 г.)).
Здесь sqrt — обозначение знака квадратного корня из числа.

вычисления n-й степени числа X. Вычисление описать каждым из

трех вариантов оператора цикла: For... to...do, While… do, Repeat… until.
Задача 2. Вычислив асимптотический ряд  S= 1-1/3 +1/5 -1/7 + 1/9 - … (-1)i+1 (1/(2i+1))... с точностью eps=0.0001 , вы узнаете, чему равно число π = 4*S . Напишите программу вычисления числа π и сравните со значением π, вычисленным с помощью стандартной функции Pi.
Замечание. Здесь удобно использовать такую формулу для нечетного числа: i:=i+2 (i=1, 2, 3...).