Слайд 2
Содержание
Текущий контроль
Часть 1. Общие положения теории игр и
их классификация.
Часть 2. Примеры игр.
Часть 3. Эквивалентные преобразования игр.
Часть
4. Поиск решения игр в чистых стратегиях.
Часть 5. Поиск решения игр в смешанных стратегиях (алгоритм Брауна-Робинсона).
Слайд 3
Текущий контроль
Прогнозировать результаты голосования с помощью дерева вариантов,
если число голосов каждой коалиции определяется номером студента k.
Слайд 4
Часть 1
Общие положения теории игр и их классификация
Слайд 5
Основные компоненты любой игры
конфликт;
принятие решения;
оптимальность
решения.
Слайд 6
Характеризующие игру элементы
чередование либо одновременность ходов, которые могут
быть, как логичными, так и случайными;
возможная недостаточность информации;
функция выигрыша, определяющая цену игры.
Слайд 7
Классификация игр
Матричные и позиционные;
Антагонистические и неантагонистические;
С полной и
неполной информацией;
Игры двух и более лиц;
Игры с коалициями и
без них;
Игры в чистых и смешанных стратегиях;
Игры с нулевой и произвольной суммой;
Игры с седловой точкой и без нее;
Конечные и бесконечные игры…
Слайд 9
Антагонистические и неантагонистические игры
Антагонистическая игра: матричная игра с
полной информацией и нулевой суммой
Неантагонистическая игра: первый игрок выбирает
наилучшую для себя стратегию, второй –выбирает ее случайно.
«Игра с болваном»: первый игрок выбирает наилучшую для себя стратегию, второй действует в интересах первого игрока.
Слайд 10
Теорема о предательстве
Игрок вступивший в коалицию и нарушивший
ее рискует проиграть все.
Слайд 11
Дилемма заключенного
Каждому из двух заключенных, обвиняемых в одном
преступлении, предлагается на выбор три альтернативы:
Признать вину – тогда
он получит срок t лет, а другой заключенный выйдет на свободу.
Не признавать вину, тогда ему грозит срок Т лет.
Обвинить в преступлении другого заключенного, тогда обвинивший будет выпущен на свободу, а другой заключенный получит срок Т лет.
Слайд 12
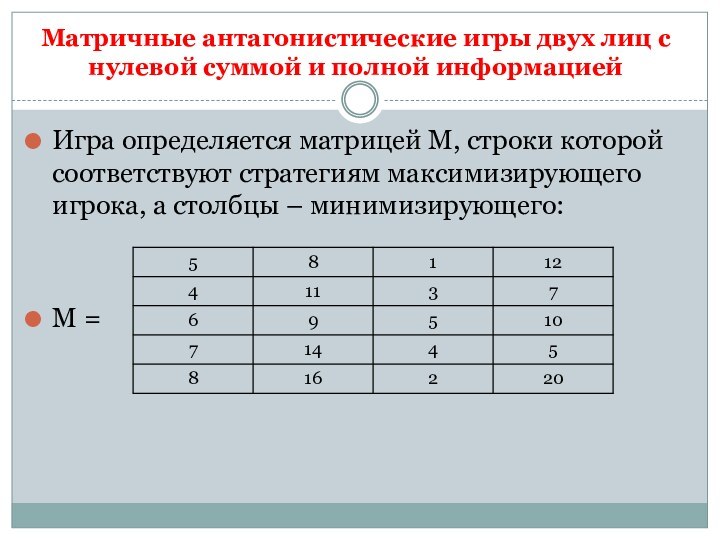
Матричные антагонистические игры двух лиц с нулевой суммой
и полной информацией
Игра определяется матрицей М, строки которой соответствуют
стратегиям максимизирующего игрока, а столбцы – минимизирующего:
М =
Слайд 13
Часть 3
Эквивалентные преобразования игр
Слайд 14
Доминирующая и доминируемая стратегии
Стратегии i и j называются
соответственно доминирующей и доминируемой, если каждый элемент i-ой стратегии
“лучше” одноименного элемента j-ой стратегии. Это позволяет игнорировать доминируемые стратегии и, таким образом, облегчить поиск оптимальных стратегий игроков.
Слайд 15
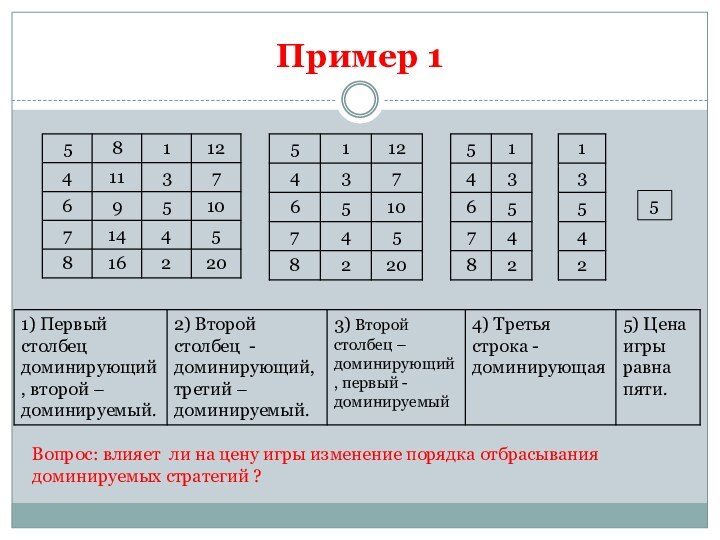
Пример 1
5
Вопрос: влияет ли на цену игры
изменение порядка отбрасывания доминируемых стратегий ?
Слайд 16
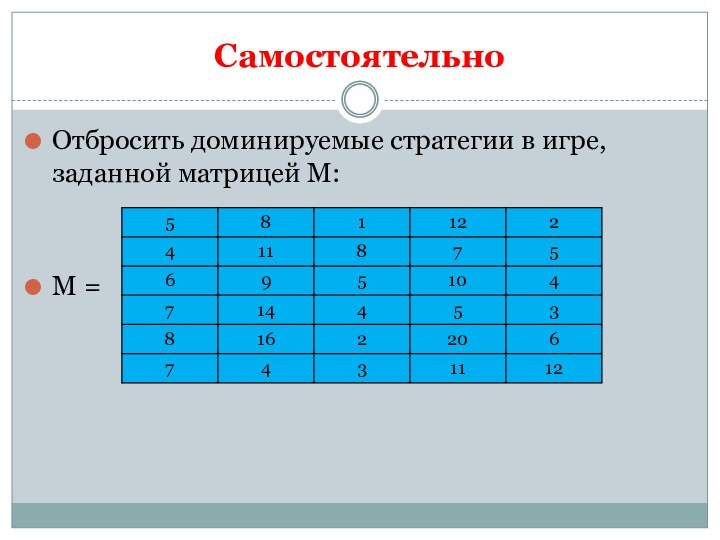
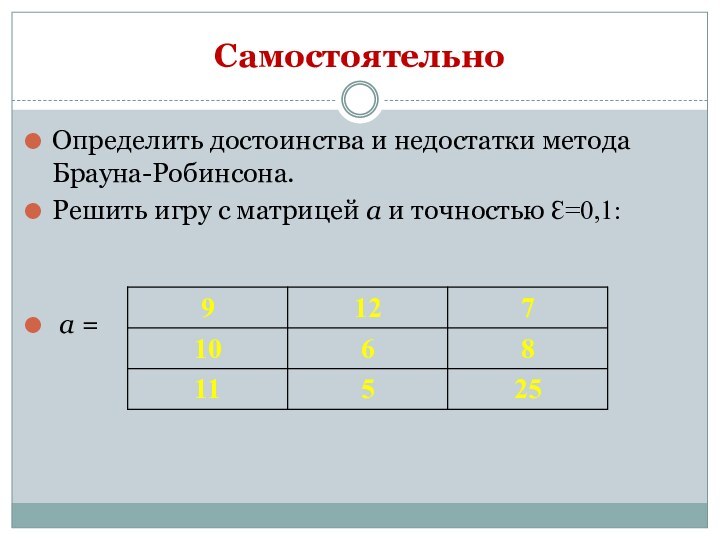
Самостоятельно
Отбросить доминируемые стратегии в игре, заданной матрицей М:
М
Слайд 17
Часть 4
Поиск решения игры в чистых стратегиях
Слайд 18
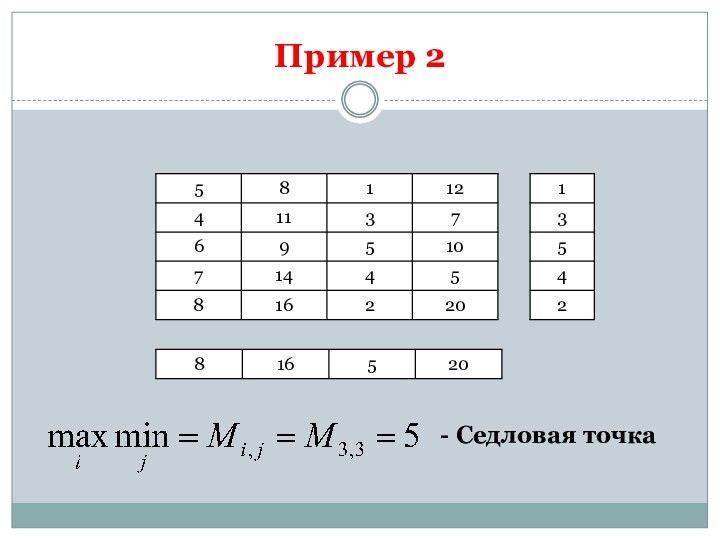
Равновесные стратегии
Ситуация (пара стратегий) называется равновесной, если соответствующий
ей элемент матрицы игры является одновременно наибольшим в своем
столбце и наименьшим в своей строке.
Слайд 20
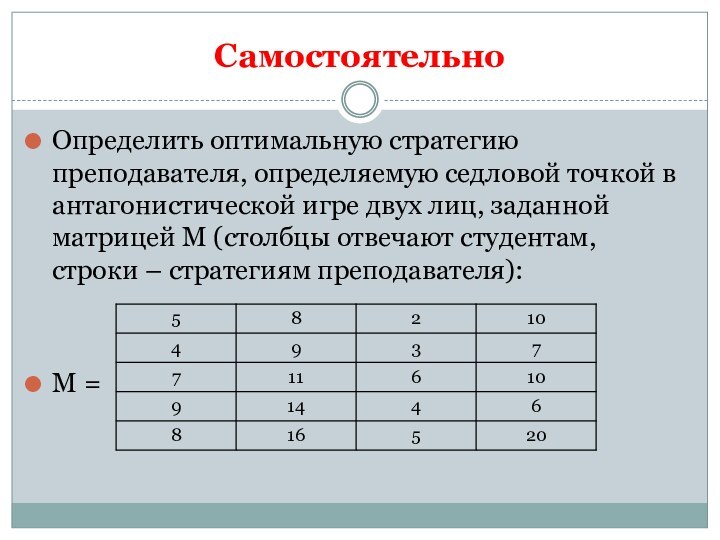
Самостоятельно
Определить оптимальную стратегию преподавателя, определяемую седловой точкой в
антагонистической игре двух лиц, заданной матрицей М (столбцы отвечают
студентам, строки – стратегиям преподавателя):
М =
Слайд 21
Гарантирующие стратегии
Гарантирующие стратегии применяются в играх с полной
информацией, когда отсутствует седловая точка.
Применительно к каждому игроку гарантирующей
является стратегия, обеспечивающая ему лучшую цену игры из худших.
Слайд 22
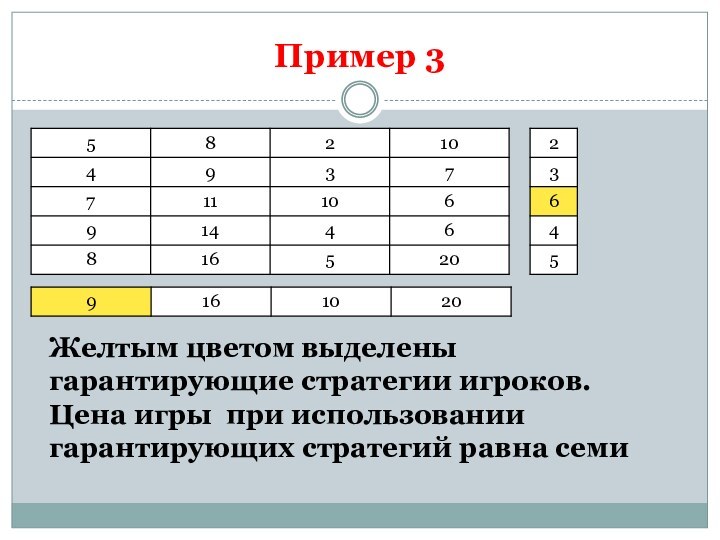
Пример 3
Желтым цветом выделены гарантирующие стратегии игроков.
Цена игры
при использовании гарантирующих стратегий равна семи
Слайд 23
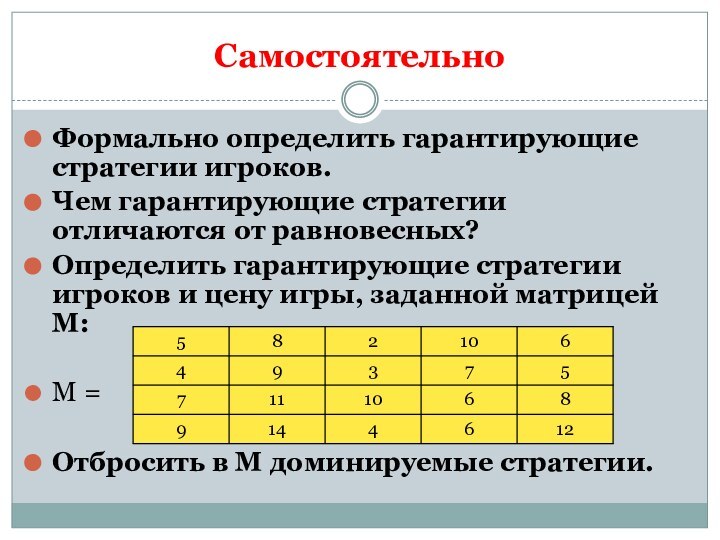
Самостоятельно
Формально определить гарантирующие стратегии игроков.
Чем гарантирующие стратегии отличаются
от равновесных?
Определить гарантирующие стратегии игроков и цену игры, заданной
матрицей М:
М =
Отбросить в М доминируемые стратегии.
Слайд 24
Часть 5
Поиск решения игры в смешанных стратегиях
Слайд 25
Смешанные стратегии
Игры с полной информацией, т.е. такие, в
которых каждый игрок знает возможности и “наклонности” противника, реализуются,
как в чистых, так и в смешанных стратегиях. В первом случае каждый игрок в ходе игры может придерживаться только одной, выбранной им стратегии, а во втором – нескольких стратегий, применительно к которым фиксируются лишь вероятности их выбора. Цель многоходовой антагонистической матричной игры с полной информацией состоит в определении оптимальных вероятностей выбора стратегий каждым из игроков.
Слайд 26
Формальная постановка задачи поиска оптимальной смешанной стратегии
Пусть -
вероятность выбора i –ой стратегии одним игроком, а -
вероятность выбора j –ой стратегии другим игроком. Цена игры V(Г) при фиксированных стратегиях и равна:
Слайд 27
Теорема о минимаксе
Справедлива теорема о минимаксе, в некотором
смысле аналогичная теореме о седловой точке для матричной игры
в чистых стратегиях:
Слайд 28
Метод Брауна-Робинсона
Идея метода заключается в том, что игра
разыгрывается много раз, причем при каждом разыгрывании каждый игрок
фиксирует эмпирические вероятности стратегий противника: если II игрок использовал j –ю стратегию qi раз, то игрок I выбирает i так, чтобы максимизировать . Аналогично, если игрок I использовал i –ую стратегию pi раз, то игрок II выбирает j так, чтобы минимизировать .
Доказано, что с ростом числа разыгрываний эмпирические распределения сходятся к оптимальным стратегиям.
Слайд 29
Алгоритм Брауна-Робинсона
Шаг 1. Ввод матрицы игры «а» и
точности Ɛ.
Шаг 2.
Шаг 3.
Шаг 4. Определяется цена игры
Шаг
5. S= ∞.
Шаг 6. Выбор такого i, для которого сумма D=
максимальна (i=A).
Шаг 7. Выбор такого j=B, для которого сумма С =
минимальна.
Слайд 30
Алгоритм Брауна-Робинсона (продолжение)
Шаг 8. ха=ха+1.
Шаг 9. yв=yв+1.
Шаг 10.
Вычисляется новая цена игры V1 :
Шаг 11. Если
, то перейти к шагу 14, в противном случае – к шагу 12.
Шаг 12. V0=V1
Шаг 13. Перейти к шагу 6.
Шаг 14. Конец алгоритма, печать векторов Х и У.
Слайд 31
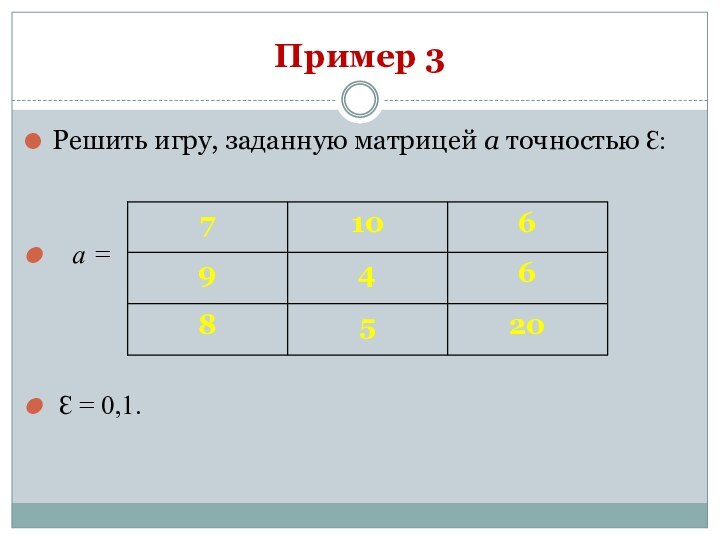
Пример 3
Решить игру, заданную матрицей а точностью Ɛ:
а =
Ɛ = 0,1.
Слайд 32
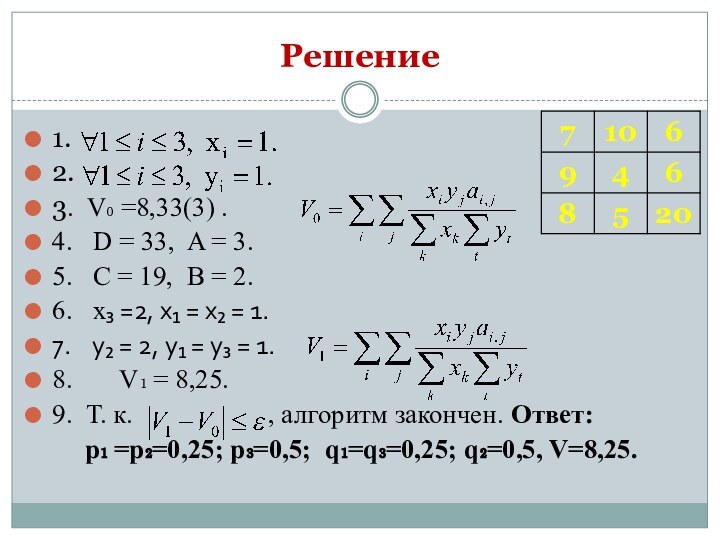
Решение
1.
2.
3. V₀ =8,33(3) .
4. D
= 33, A = 3.
5. C = 19, B = 2.
6. x₃ =2, x₁ = x₂ = 1.
7. y₂ = 2, y₁ = y₃ = 1.
8. V₁ = 8,25.
9. Т. к. , алгоритм закончен. Ответ:
p₁ =p₂=0,25; p₃=0,5; q₁=q₃=0,25; q₂=0,5, V=8,25.