- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Игры с полной информацией
Содержание
- 2. Игра с полной информацией — термин, обозначающий логическую игру, в которой для соперников отсутствует элемент неопределённости.
- 3. Игра является игрой с полной информацией, еслиигроки
- 4. Если ни в каких аспектах игры (правилах,
- 5. Стратегиястратегия игрока в игре — это полный
- 6. Для любой детерминированной игры с полной информацией,
- 7. К играм с полной информацией относятся детерминированные
- 8. Крестики-нолики Правила игры Игроки по очереди ставят
- 9. Общеизвестный алгоритм, который при правильной игре гарантирует
- 10. За крестики Сделать первый ход в центральное
- 11. За крестики Или: Сделать первый ход в
- 12. За нолики. Если противник сходил первым ходом
- 13. Игра «Спички» сначала в кучке лежит 5
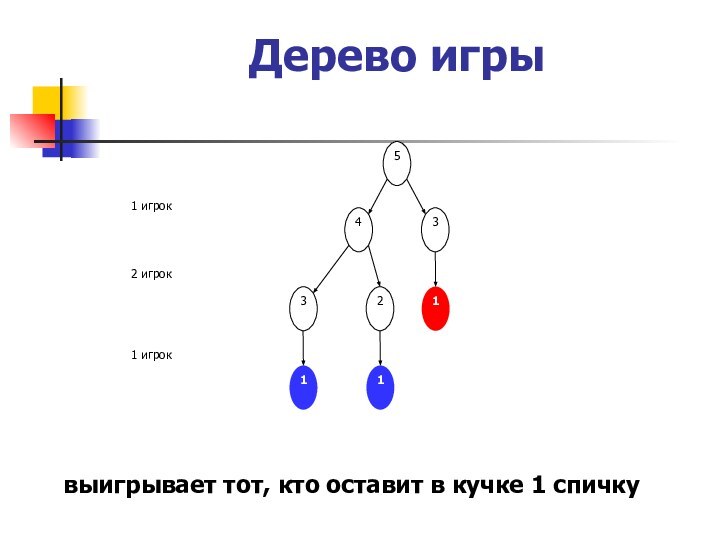
- 14. Дерево игрывыигрывает тот, кто оставит в кучке 1 спичку
- 15. простроенная схема называется «деревом игры», она показывает
- 16. Задача 1
- 17. Каким должен быть первый ход выигравшего игрока?Каждый
- 18. «Поиск в глубины»при первом ходе I-ого игрока
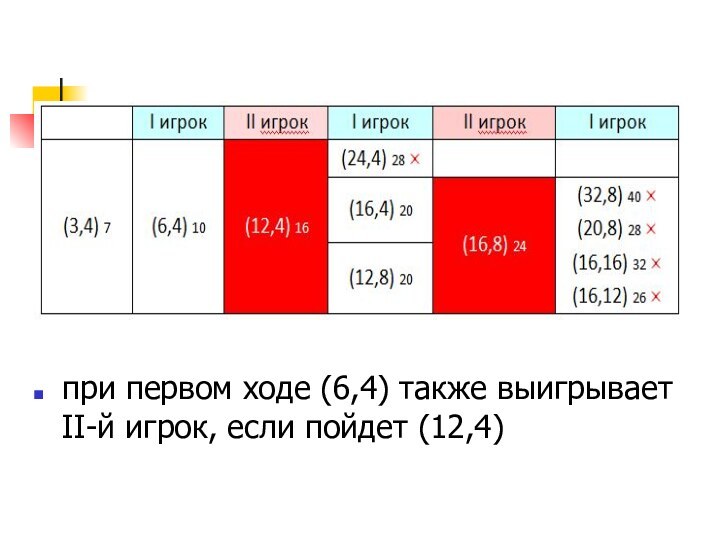
- 19. при первом ходе (6,4) также выигрывает II-й игрок, если пойдет (12,4)
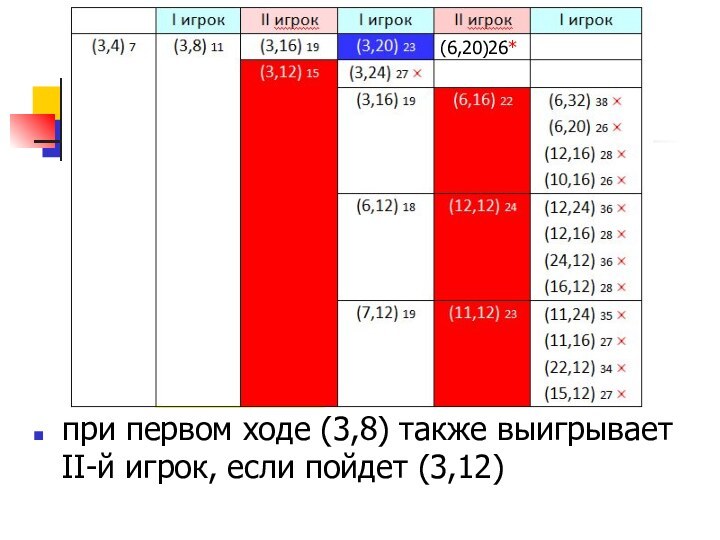
- 20. при первом ходе (3,8) также выигрывает II-й игрок, если пойдет (3,12)(6,20)26*
- 21. Выигрышная стратегияВыигрывает II-й игрок; своим первым ходом
- 25. Задача 2.Два игрока играют в следующую игру.
- 26. из каждой ситуации в этой игре возможно
- 28. Скачать презентацию
- 29. Похожие презентации
Игра с полной информацией — термин, обозначающий логическую игру, в которой для соперников отсутствует элемент неопределённости.



















Слайд 2 Игра с полной информацией — термин, обозначающий логическую
игру, в которой для соперников отсутствует элемент неопределённости.
Слайд 3
Игра является игрой с полной информацией, если
игроки воздействуют
на игровую ситуацию дискретными действиями — ходами, порядок ходов
определён правилами и не зависит от таких параметров, как скорость реакции игроков (то есть очередной ход делает тот, кто должен его сделать по правилам, а не тот, кто первым догадался или успел его сделать);в любой момент игры все игроки имеют полную информацию о состоянии игры, то есть о позиции и всех возможных ходах любого из игроков.
Слайд 4 Если ни в каких аспектах игры (правилах, возможности
или очерёдности ходов, определении момента завершения игры или результата)
не участвует элемент случайности, такая игра будет детерминированной.
Слайд 5
Стратегия
стратегия игрока в игре — это полный план
действий при всевозможных ситуациях, способных возникнуть. Стратегия определяет действие
игрока в любой момент игры и для каждого возможного течения игры, способного привести к каждой ситуации.Набор стратегий — стратегии для каждого из игроков, которые полностью описывают все действия в игре. Набор стратегий обязан включать одну и только одну стратегию для каждого игрока.
Слайд 6 Для любой детерминированной игры с полной информацией, теоретически,
можно просчитать все возможные ходы игроков и определить последовательность
ходов (алгоритм), которая гарантированно приведёт по крайней мере одного из них к выигрышу или ничьей.Слайд 7 К играм с полной информацией относятся детерминированные настольные
игры (например, шахматы, шашки, крестики-нолики и др.).
Для большинства
из них алгоритм выигрыша или гарантированной ничьей неизвестен, хотя теоретически он существует. На практике вариантов слишком много, чтобы их можно было построить и проанализировать за приемлемое время.
Слайд 8
Крестики-нолики
Правила игры
Игроки по очереди ставят на
свободные клетки поля свои знаки (крестики и нолики соответственно).
Первый, выстроивший в ряд 3 своих фигуры по вертикали, горизонтали или диагонали, выигрывает.Первый ход делает игрок, ставящий крестики.
Слайд 9 Общеизвестный алгоритм, который при правильной игре гарантирует ничью
любой стороне, а при ошибке противника позволяет выиграть.
Данный
алгоритм предполагает оптимальную игру противника.
Слайд 10
За крестики
Сделать первый ход в центральное поле.
Противник может ответить ходом либо в угол, либо на
сторону поля. Если противник ответил ходом в угловое поле — сходить в ответ в соседний угол.
Противник будет вынужден пойти в противоположный угол, чтобы на следующем ходу не проиграть.
Дальнейшие ходы делаются так, чтобы блокировать построение тройки противником. — Ничья.
Если противник ответил ходом на сторону — он проиграл. Следует ответить ходом в угол.
Противник будет вынужден пойти в противоположный угол, чтобы на следующем ходу не проиграть.
Сходить в угол, соседний с предыдущим, так, чтобы крестики образовали треугольник — получится «вилка», позволяющая следующим ходом построить тройку двумя способами.
Как бы ни ответил противник, следующим ходом строится одна из троек. — Выигрыш.
Слайд 11
За крестики
Или:
Сделать первый ход в угол.
Противник может ответить либо ходом на сторону, либо ходом
в угол, либо ходом в центр. Если противник ответил ходом на сторону, он проиграл. Следует ответить ходом в центр, сводя к предыдущей стратегии. - Выигрыш.
Если противник ответил ходом в угол, он вновь проигрывает. Следует ответить ходом в любой из оставшихся углов.
Противник будет вынужден блокировать угрозу, следующим ходом нужно занять последний угол, что дает вилку. - Выигрыш.
Если противник ответил ходом в центр, то нужно занять угол противоположный первому углу. Противник может ответить либо ходом на сторону, либо ходом в угол.
Если противник ответил ходом в угол, он проиграл -- следует немедленно занять другой угол, блокируя тройку противника и образуя свою вилку. - Выигрыш.
Если противник ответил ходом на сторону, то следующие ходы строятся так, чтобы блокировать тройки соперника - Ничья.
Слайд 12
За нолики.
Если противник сходил первым ходом в
центр, ответить ходом в любой из углов, затем каждым
следующим ходом блокировать возможность построения противником очередной тройки, при возможности выбора предпочитая ходы в углы. — Ничья.Если противник сходит первым ходом не в центр, ответить ходом в центр. Если ответным ходом противник займёт два противоположных угла, ответить ходом на сторону. Затем каждым следующим ходом блокировать возможность построения противником очередной тройки, при возможности выбора предпочитая ходы в углы. — Ничья.
Слайд 13
Игра «Спички»
сначала в кучке лежит 5 спичек;
два игрока убирают спички по очереди, причем за 1
ход можно убрать 1 или 2 спички;Слайд 15 простроенная схема называется «деревом игры», она показывает все
возможные варианты, начиная с некоторого начального положения
при правильной игре
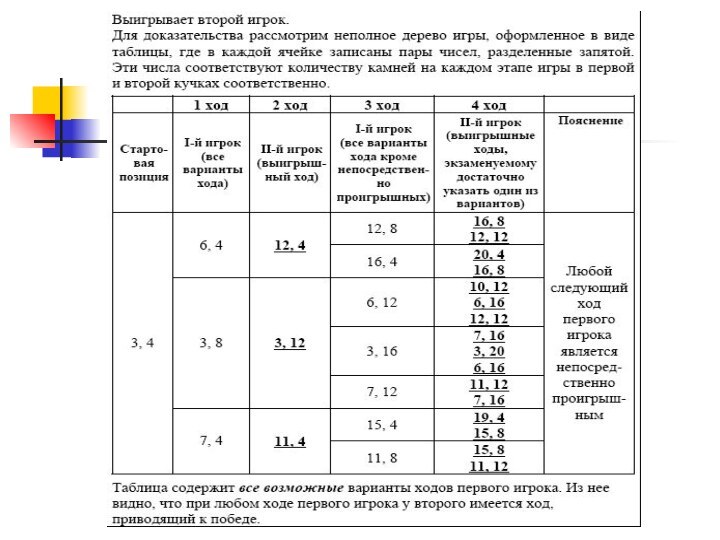
выиграет первый игрок, для этого ему достаточно первым ходом убрать всего одну спичку
Слайд 17
Каким должен быть первый ход выигравшего игрока?
Каждый хочет
выиграть!
Никто не ошибается!
Выигрыш зависит только от начального положения и
правил игры.Тот, кто получил 25 или больше камней в обоих кучках, проигрывает
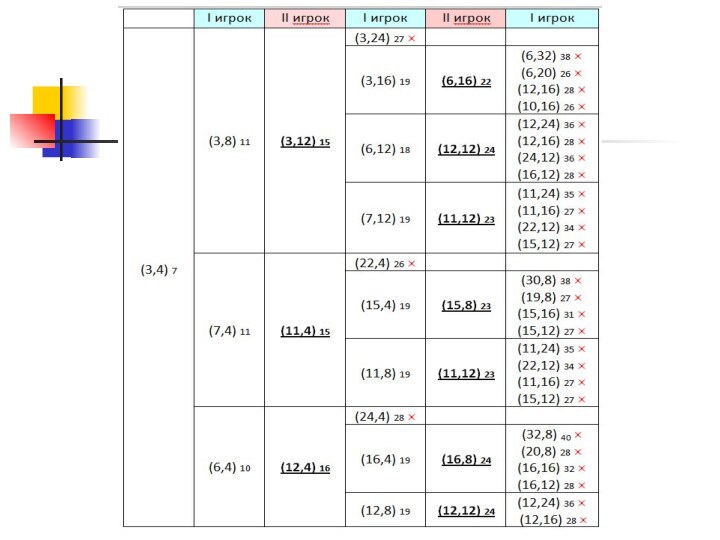
Слайд 18
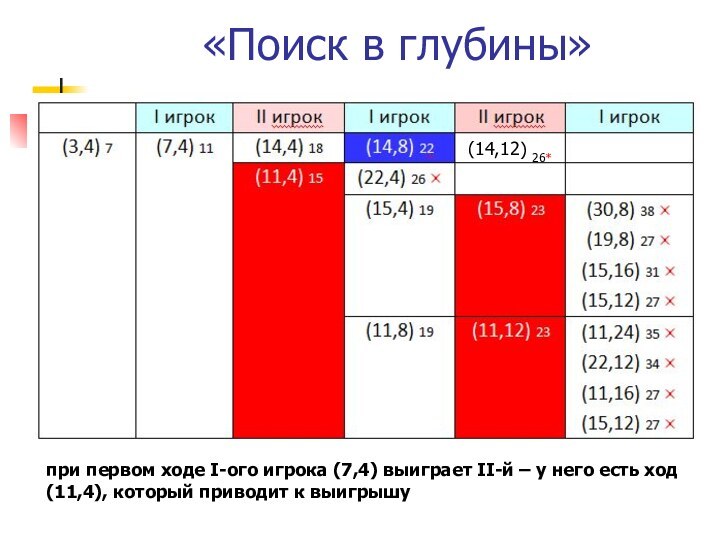
«Поиск в глубины»
при первом ходе I-ого игрока (7,4)
выиграет II-й – у него есть ход (11,4), который
приводит к выигрышу(14,12) 26*
Слайд 21
Выигрышная стратегия
Выигрывает II-й игрок;
своим первым ходом ему
нужно свести игру к позиции (11,4), (12,4) или (3,12),
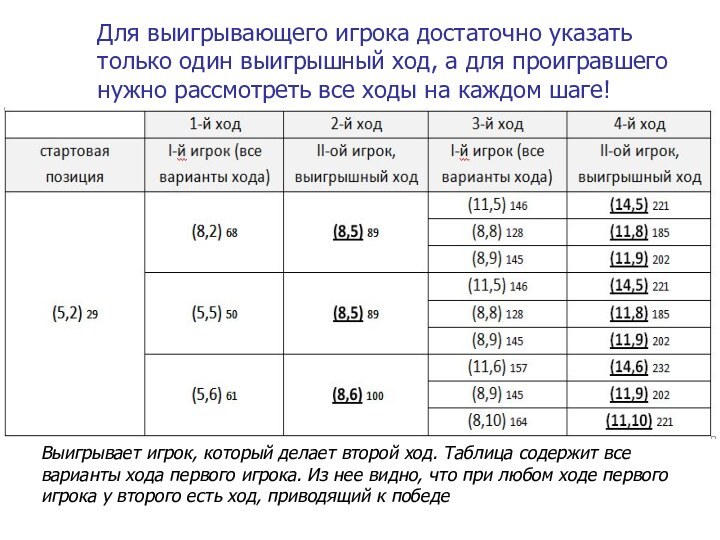
а вторым ходом – к одной из позиций (15,8), (16,8), (11,12), (12,12) или (6,16).Для выигрывающего игрока достаточно указать только один выигрышный ход, а для проигравшего нужно рассмотреть все ходы на каждом шаге!
Слайд 25
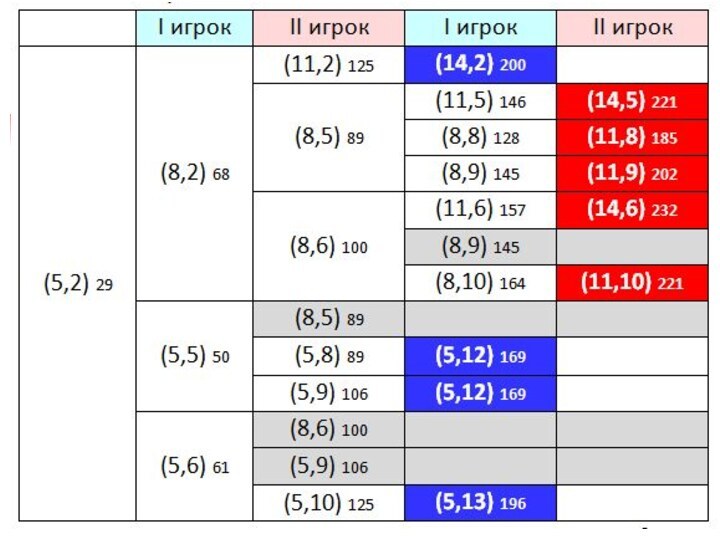
Задача 2.
Два игрока играют в следующую игру. На
координатной плоскости стоит фишка. Игроки ходят по очереди. В
начале игры фишка находится в точке с координатами (5,2). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: или в точку с координатами (x+3,y), или в точку с координатами (x,y+3), или в точку с координатами (x,y+4). Выигрывает игрок, после хода которого расстояние по прямой от фишки до точки с координатами (0,0) не меньше 13 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.Слайд 26 из каждой ситуации в этой игре возможно три
продолжения
по теореме Пифагора расстояние L от точки с координатами
(x,y) до начала координат – это илив начальный момент
условие не выполнено





























