- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математическая модель
Содержание
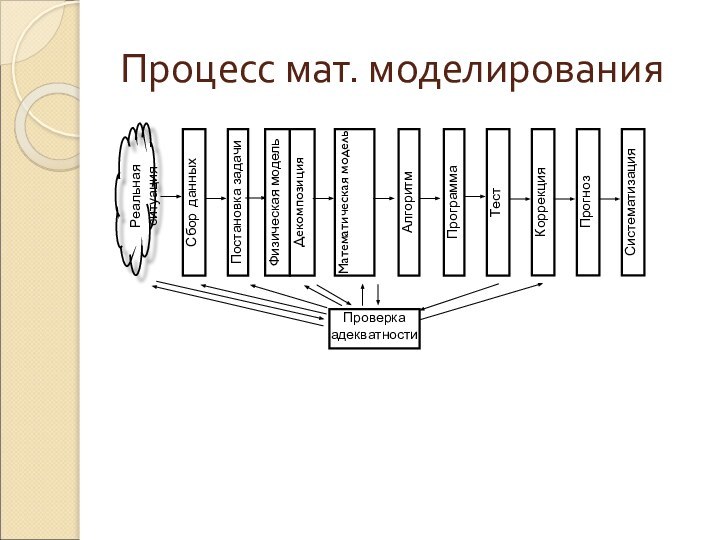
- 2. Процесс мат. моделированияСистематизацияРеальная ситуацияСбор данныхПостановка задачиФизическая модельДекомпозицияМатематическая модельАлгоритмПрограммаТестКоррекцияПрогнозПроверка адекватности
- 3. Формулировка математической модели явленияМатематическая модель любого изучаемого
- 4. Проведение математического исследованияНа этом этапе моделирования, в
- 5. Математическое исследование моделиМатематическое исследование моделиАналитические методыЧисленные методыЧисленное решение на ЭВМАналитическое решениеСимвольные вычисления на ЭВМАдекватность модели
- 6. Использование ЭВМ в процессе математического исследования модели
- 7. Источники погрешности решенияМатематическая модельИсходные данныеПриближенный методПогрешности вычислений
- 8. 1. Погрешность мат. моделиМатематические формулировки редко точно
- 9. 2. Погрешности исходных данныхВызваны наличием в математических
- 10. 3. Погрешности методаПоскольку аналитически решить задачу невозможно,
- 11. 4. Погрешности вычисленийПри вычислениях на ЭВМ неизбежны
- 12. Числа с плавающей точкойСовременные компьютеры позволяют обрабатывать
- 13. Числа с плавающей точкойПри решении научно-технических задач
- 14. Понятие погрешностиАбсолютная погрешность – разность между истинным
- 15. Предельная погрешностьОчень часто истинное значение х неизвестно
- 16. Правила округленияОкругление до n значащих цифр –
- 17. Правила округленияЕсли первая из отброшенных цифр равна
- 18. Правила округленияПри применении правил округления погрешность не превосходит половины десятичного разряда последней оставленной цифры
- 19. Действия над приближенными числамиПри сложении и вычитании
- 20. Примерa = 2520, b = 2518,
- 21. Уменьшение погрешностейИзбегать вычитания близких по значению чиселПрименять правильный порядок вычисленийПравильно использовать ряды для вычисления функций
- 22. Порядок вычисленийS = 0.2764+0.3944+1.475+26.46+1364=1393Компьютер округляет после каждого
- 23. Скачать презентацию
- 24. Похожие презентации
Процесс мат. моделированияСистематизацияРеальная ситуацияСбор данныхПостановка задачиФизическая модельДекомпозицияМатематическая модельАлгоритмПрограммаТестКоррекцияПрогнозПроверка адекватности






















Слайд 2
Процесс мат. моделирования
Систематизация
Реальная ситуация
Сбор данных
Постановка задачи
Физическая модель
Декомпозиция
Математическая модель
Алгоритм
Программа
Тест
Коррекция
Прогноз
Проверка
адекватности
Слайд 3
Формулировка математической модели явления
Математическая модель любого изучаемого явления,
по причине его чрезвычайной сложности, должна охватывать важнейшие для
рассматриваемой задачи стороны процесса, его существенные характеристики и формализованные связи, подлежащие учёту.Как правило, математическая модель изучаемого физического явления формулируется в виде уравнений математической физики. Чаще всего это нелинейные, многомерные системы уравнений, содержащие большое число неизвестных и параметров.
Если математическая модель выбрана недостаточно тщательно, то какие бы мы не применяли методы для дальнейших расчётов, полученные результаты будут ненадежны, а в отдельных случаях и совершенно неверны.
Слайд 4
Проведение математического исследования
На этом этапе моделирования, в зависимости
от сложности рассматриваемой модели, применяют различные подходы к её
исследованию и различный смысл вкладывается в понятие решения задачи.Для наиболее грубых и несложных (относительно) моделей удаётся получить их аналитическое – общее – решение.
Для более точных и сложных моделей основными методами решения являются численные методы решения с необходимостью требующие проведения большого объёма вычислений на ЭВМ. Эти методы позволяют добиться хорошего количественного и даже качественного результата в описании модели. Но, правда, у них есть и принципиальные недостатки – как правило, речь идёт о рассмотрении некоторого частного решения.
Слайд 5
Математическое исследование модели
Математическое исследование модели
Аналитические методы
Численные методы
Численное решение
на ЭВМ
Аналитическое решение
Символьные вычисления на ЭВМ
Адекватность модели
Слайд 6
Использование ЭВМ в процессе математического исследования модели требует
специфических, численных методов, т.е. такой "интерпретации" математической модели, которая
может быть реализована на ЭВМ - назовём её дискретной (или вычислительной) моделью. Поскольку ЭВМ выполняет только арифметические и логические операции, то для реализации вычислительной модели требуется разработка соответствующего вычислительного алгоритма, собственно программирование, расчет на ЭВМ, обработка результатов расчета.
Слайд 7
Источники погрешности решения
Математическая модель
Исходные данные
Приближенный метод
Погрешности вычислений
Слайд 8
1. Погрешность мат. модели
Математические формулировки редко точно отражают
реальные явления, обычно они дают лишь более или менее
идеализированные модели. Как правило, при изучении тех или иных явлений мы вынуждены допустить некоторые упрощения, что и вызывает появление погрешностей решения
Слайд 9
2. Погрешности исходных данных
Вызваны наличием в математических формулах
числовых параметров, значения которых могут быть определены лишь приближенно.
Это, например, все физические константы или экспериментальные результаты, используемые в модели
Слайд 10
3. Погрешности метода
Поскольку аналитически решить задачу невозможно, ее
приходится заменять некоторой приближенной задачей, дающей близкие результаты. Например,
интеграл заменяют суммой, производную – разностью, функцию – многочленом и т.д. Еще один источник – применение бесконечных итерационных процессов, принудительно прерываемых (например, sin x = x – x3/3!+x5/5! – …)
Слайд 11
4. Погрешности вычислений
При вычислениях на ЭВМ неизбежны погрешности,
связанные с ограниченностью разрядной сетки машины – погрешности округлений
(δmax = 0.5α1-k, α − основание системы счисления) и с переводом чисел из одной системы счисления в другую
Слайд 12
Числа с плавающей точкой
Современные компьютеры позволяют обрабатывать целые
числа и числа с плавающей точкой.
Множество целых чисел бесконечно,
но из-за ограниченной разрядной сетки мы можем оперировать только с конечным подмножеством. При 4-х байтах на число диапазон доступных чисел составляет ~ от −2.109 до 2.109
Слайд 13
Числа с плавающей точкой
При решении научно-технических задач в
основном используются вещественные числа. Пример: 273.9
2739.10-1
2.739.102
0.2739.103
Последняя запись – нормализованная
форма числа с плавающей точкой. Общий вид:
D = ±m . 10n, m=0.d1d2… dk, d1≠0m – мантисса, n – порядок числа
Слайд 14
Понятие погрешности
Абсолютная погрешность – разность между истинным значением
числа и приближенным. Если а – приближенное значение х: Δx
= |a – x|Относительная погрешность – отношение абсолютной погрешности к приближенному значению δx = Δx/a
Слайд 15
Предельная погрешность
Очень часто истинное значение х неизвестно и
приведенные выражения невозможно использовать. В этом случае используют верхнюю
оценку модуля абсолютной погрешности, называемую предельной погрешностью Δа: Δx ≤ ΔаВ дальнейшем Δа принимается в качестве абсолютной погрешности
Слайд 16
Правила округления
Округление до n значащих цифр – отбрасывание
всех цифр справа от n-й
Если первая из отброшенных цифр
меньше 5, то оставшиеся цифры остаются без изменения (8,3 ≈ 8)Если первая из отброшенных цифр больше 5, то к последней оставшейся цифре добавляется 1 (8,6 ≈ 9)
Слайд 17
Правила округления
Если первая из отброшенных цифр равна 5
и среди остальных отброшенных имеются ненулевые, то к последней
оставшейся цифре добавляется 1 (8,501 ≈ 9)Если первая из отброшенных цифр равна 5 и все остальные – нули, то последняя оставшаяся остается неизменной, если она четная, и увеличивается, если нечетная (6,5 ≈ 6, но 7,5 ≈ 8)
Слайд 18
Правила округления
При применении правил округления погрешность не превосходит
половины десятичного разряда последней оставленной цифры
Слайд 19
Действия над приближенными числами
При сложении и вычитании чисел
их абсолютные погрешности складываются: Δ(a ± b) = Δa
+ ΔbПри умножении и делении чисел их относительные погрешности складываются: δ(a . b) = δa + δb δ(a / b) = δa + δb
При возведении числа в степень его относительная погрешность умножается на показатель степени δ(ak) = kδa
Слайд 20
Пример
a = 2520, b = 2518, a
– b = 2
Δa = Δb = 0.5
δa =
0.5/2520 ≈ 0.0002 (0.02%)δb = 0.5/2518 ≈ 0.0002 (0.02%)
Относительная погрешность разности
δ(a − b) = (0.5 + 0.5)/2 = 0.5 (50%)
Слайд 21
Уменьшение погрешностей
Избегать вычитания близких по значению чисел
Применять правильный
порядок вычислений
Правильно использовать ряды для вычисления функций
Слайд 22
Порядок вычислений
S = 0.2764+0.3944+1.475+26.46+1364=1393
Компьютер округляет после каждого сложения,
поэтому законы коммутативности выполняются не всегда. При обратном порядке
сложения получимS = 1364+26.46+1.475+0.3944+0.2764= 1391