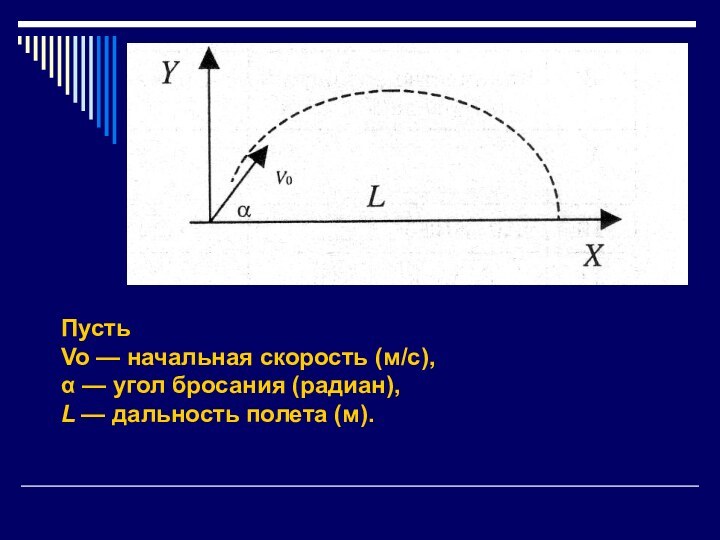
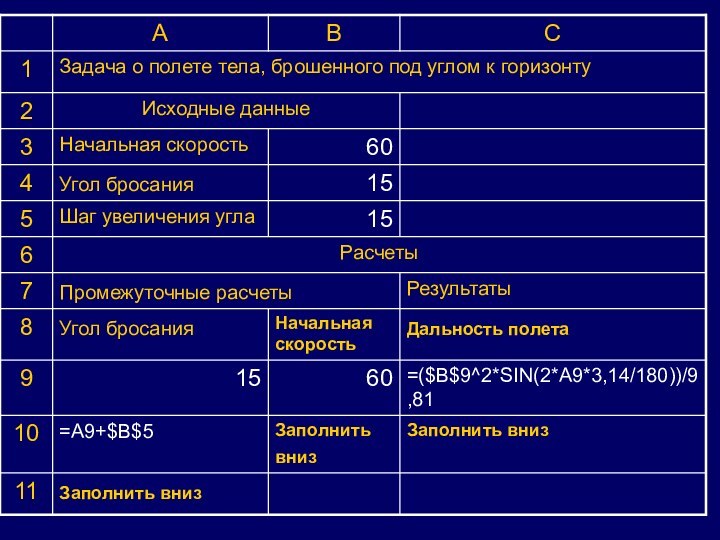
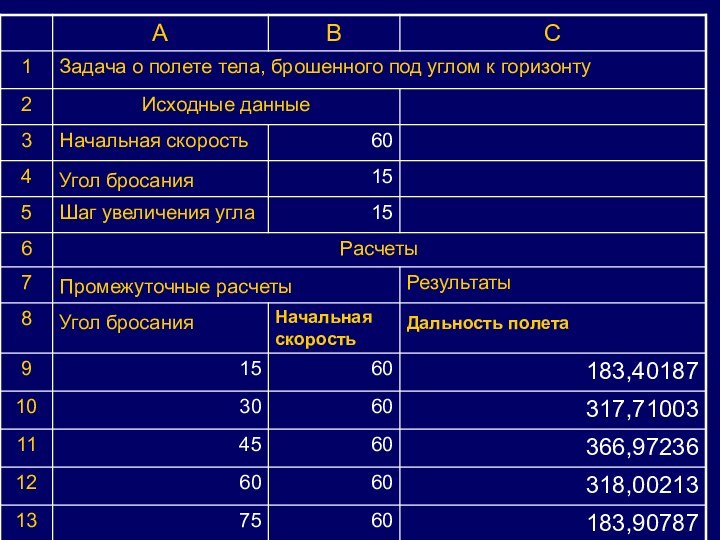
брошенного под углом к горизонту.
Выяснить зависимость расстояния и
времени полета тела от угла броска и начальной скорости. Угол броска и начальная скорость являются главными факторами процесса моделирования.