Слайд 2
Раздел 7. Анализ переходного процесса
ВВЕДЕНИЕ В АНАЛИЗ ПЕРЕХОДНОГО
ПРОЦЕССА…..……………………..7 - 4
ПРЯМОЙ МЕТОД АНАЛИЗА………………………………………………………..7 - 5
ДЕМПФИРОВАНИЕ ПРИ ПРМОМ
МЕТОДЕ АНАЛИЗА.……………………….7 - 9
МОДАЛЬНЫЙ МЕТОД АНАЛИЗА..………………………………………………..7 - 10
ДЕМПФИРОВАНИЕ ПРИ МОДАЛЬНОМ МЕТОДЕ АНАЛИЗА.……………….7 - 12
ВЫЧИСЛЕНИЕ РЕЗУЛЬТАТОВ ПРИ МОДАЛЬНОМ МЕТОДЕ АНАЛИЗА....7 - 17
УПРАВЛЕНИЕ МОДАМИ.…………………………………………………………….7 - 18
ЗАДАНИЕ ВНЕШНЕГО ВОЗДЕЙСТВИЯ.…………………………………………7 - 19
ОПЕРАТОР TLOAD1…………………………………………………………………..7 - 20
ОПЕРАТОР TLOAD2…………………………………………………………………..7 - 22
КОМБИНАЦИЯ НАГРУЗОК – ОПЕРАТОР DLOAD………………………..…….7 - 23
ОПЕРАТОР DAREA……………………………………………………………………7 - 24
ПРИМЕР ОПЕРАТОРА DAREA.……………………………………………………..7 - 25
СТАТИЧЕСКАЯ НАГРУЗКА – НЕПРЯМОЙ МЕТОД ЗАДАНИЯ..………………7 - 26
Слайд 3
Анализ переходного процесса (продолж.)
СТАТИЧЕСКАЯ НАГРУЗКА – ПРЯМОЙ МЕТОД
ЗАДАНИЯ..………………….…7 - 28
ЗАМЕЧАНИЯ К СПОСОБУ ЗАДАНИЮ ВНЕШНЕГО ВОЗДЕЙСТВИЯ………….7 -
30
НАЧАЛЬНЫЕ УСЛОВИЯ.………………………………………………………………..7 - 32
ОПЕРАТОР TSTEP…...…………………………………………………………………...7 - 35
МЕТОДЫ ВЫЧИСЛЕНИЯ РЕЗУЛЬТАТОВ...…………………………………………7 - 38
ПРИМЕНЕНИЕ МОДАЛЬНОГО И ПРЯМОГО МЕТОДОВ АНАЛИЗА..…………..7 - 39
УПРАВЛЕНИЕ РЕШЕНИЕМ ПРИ АНАЛИЗЕ ПЕРЕХОДНОГО ПРОЦЕССА..…..7 - 40
ВИДЫ ВЫЧИСЛЯЕМЫХ ВЕЛИЧИН………..………………………………………….7 - 42
ПРИМЕР №3 – АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА ПРЯМЫМ МЕТОДОМ…7 - 43
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №3….………………………………………….7 - 45
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №3…….…………………………………..7 - 46
ПРИМЕР №4 – АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА МОДАЛЬНЫМ МЕТОДОМ………………………………………………………………………...…………7 - 51
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №4.…………………………………………….7 - 53
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №4..………………………………………..7 - 55
Слайд 4
Введение в анализ переходного процесса
Вычисление отклика на воздействие,
зависящее от времени.
Воздействие в явной форме зависит от времени.
Все приложенные воздействия известны в любой момент времени.
Вычисляются, обычно перемещения и ускорения узлов, силы и напряжения в элементах.
Два типа анализа – прямой и модальный.
Слайд 5
Прямой метод анализа
Уравнение колебаний
Отклик вычисляется в дискретные моменты
времени с шагом .
Для представления
и в дискретные моменты времени используется метод центральных конечных разностей
Примечание: эти же уравнения используются в MSC.Nastran для вычисления скоростей и ускорений при подсчете результатов.
Слайд 6
Прямой метод анализа
Для численного интегрирования используется метод центральных
разностей (с учетом осреднения внешнего воздействия по трем последовательным
моментам времени)
Слайд 7
Прямой метод анализа
Решение
Решается путем декомпозиции матрицы A1 и
умножения на правую часть вышеприведенного уравнения.
Метод аналогичен классическому методу
Newmark-Beta.
Слайд 8
Прямой метод анализа
Матрицы M, B и K неизменны
во времени.
Если Δt неизменно в продолжении всего решения, то
декомпозицию матрицы A1 необходимо выполнять только один раз. При изменении Δt необходимо произвести повторную декомпозицию матрицы A1 (что может быть затратной операцией).
Временной интервал вывода результатов может быть больше шага решения (интегрирования) (например, при шаге решения Δt = 0,001 с и выводе результатов на каждом пятом шаге интегрирования шаг результатов будет равен 0,005 с).
Слайд 9
Демпфирование при прямом методе анализа
Матрица демпфирования B составляется
из нескольких матриц:
где B1 - элементы демпфирования (VISC,DAMP) + B2GG
B2 - прямой ввод матриц B2PP + передаточные функции
G - коэффициент глобального конструкционного
демпфирования (PARAM,G)
W3 - характерная частота - рад/с (PARAM,W3)
K1 - глобальная матрица жесткости
Ge - коэффициент конструкционного демпфирования в элементе
(параметр GE в операторе MATi)
W4 - характерная частота - рад/с (PARAM,W4)
KE - матрица жесткости элемента
В анализе переходного процесса не допустимы комплексные коэффициенты. Поэтому конструкционное демпфирование учитывается введением эквивалентного вязкого демпфирования.
По умолчанию значения параметров W3, W4 равны 0. Если пользователь не задаст им ненулевые значения, соответствующие слагаемые в приведенном уравнении будут игнорироваться.
Слайд 10
Модальный метод анализа
Преобразуем физические координаты в модальные.
(1)
Временно
пренебрежем демпфированием.
(2)
Подставим уравнение (1) в уравнение (2)
(3)
Умножим обе части
уравнения (2) слева на [φT]
(4)
где φTMφ - модальная матрица масс (диагональная)
φTKφ - модальная матрица жесткости (диагональная)
φTP - модальный вектор воздействия
Слайд 11
Модальный метод анализа
Уравнение (4) может быть записано как
для несвязанной системы с одной степенью свободы (СС):
(5)
где mi - i-я
модальная масса
ki - i-я модальная жесткость
pi - i-ое модальное воздействие
Слайд 12
Демпфирование при модальном методе анализа
Для матрицы демпфирования B
преобразование с использованием собственного вектора φ не приводит к
диагонализации результата:
Связанные задачи решаются в модальных координатах методом типа Newmark-Beta (аналогичного используемому при прямом анализе).
где
Слайд 13
Демпфирование при модальном методе анализа
При использовании модального демпфирования
каждая мода имеет коэффициент демпфирования bi.
Уравнения колебаний становятся несвязанными
Слайд 14
Демпфирование при модальном методе анализа
Модальный отклик несвязанной системы
с одной СС вычисляется с помощью интеграла Дюамеля.
Интеграл Дюамеля:
Слайд 15
Демпфирование при модальном методе анализа
Наиболее эффективно использовать модальное
демпфирование, поскольку при этом уравнения несвязанные
Оператор TABDMP1 задает коэффициент
модального демпфирования.
Type = G (по умолчанию), CRIT или Q
Например: для демпфирования, составляющего 10% от критического
Слайд 16
Демпфирование при модальном методе анализа
Оператор TABDMP1 в Bulk
Data Section инициируется оператором SDAMPING в Case Control Section.
fi
(в Гц) и gi составляют пару “частота - демпфирование”. Демпфирование для мод собственных колебаний определяется линейной интерполяцией (за пределами таблицы производится линейная экстраполяция). ENDT – символ конца таблицы.
Например: моды имеют частоты 1,0; 2,5; 3,6 и 5,5 Гц.
Может быть добавлено также немодальное демпфирование (PARAM, G; VISC; DAMP; GE в операторе MATi)
Вследствие связанности уравнений будет применено прямое интегрирование и вычислительные затраты вырастут
Практическая рекомендация: при модальном анализе переходного процесса используйте только модальное демпфирование (TABDMP1). Если необходимо дискретное демпфирование – используйте прямой анализ.
Слайд 17
Вычисление результатов при модальном методе анализа
Результат расчета в
физических координатах вычисляется путем суммирования модальных откликов.
Вычислительные затраты при
изменении Δt при модальном методе не столь высоки, как при прямом методе. Однако, по-прежнему рекомендуется постоянное значение Δt.
Шаг вывода результатов может быть больше шага решения (интегрирования).
Слайд 18
Управление модами
Могут быть необходимыми не все вычисленные моды.
Часто только небольшого количество низших мод достаточно для вычисления
динамического отклика.
Оператор PARAM,LFREQ задает нижнюю границу частотного диапазона учитываемых мод.
Оператор PARAM,HFREQ задает верхнюю границу частотного диапазона учитываемых мод.
Оператор PARAM,LMODES задает количество низших мод, учитываемых при расчете.
Неучет высших мод обуславливает отсутствие в отклике высокочастотных составляющих.
Слайд 19
Задание внешнего воздействия
Задание воздействия как функции времени.
В MSC.Nastran
предусматриваются различные методы:
TLOAD1 - “грубая сила”: табличное задание “время-сила”
TLOAD2 - эффективное
аналитическое задание
LSEQ - конвертация статических нагрузок в динамические
Слайд 20
Оператор TLOAD1
Задает воздействие в форме:
где
A - оператор (символ) пространственного
распределения воздействия и масштабного
фактора (DAREA, статическая нагрузка,
тепловая нагрузка или LSEQ)
τ - временной сдвиг (оператор DELAY)
F(t-τ) - таблица (оператор TABLEDi)
Оператор DELAY задает СС и временной сдвиг (может использоваться только с оператором DAREA).
Оператор TABLEDi задает пары “время- воздействие”.
Оператор TLOAD1 инициируется оператором DLOAD в Case Control Section.
Слайд 21
Оператор TLOAD1
Тип воздействия задается параметром TYPE.
В этом разделе
будет рассматриваться воздействие только силовыми факторами (первый ряд таблицы).
Вынужденные перемещения – см. Раздел 12.
Слайд 22
Оператор TLOAD2
Задает воздействие в форме:
где
A оператор (символ) пространственного распределения воздействия
и масштабного фактора (DAREA, статическая нагрузка, тепловая
нагрузка или LSEQ)
τ задается оператором DELAY (может использоваться только с
оператором DAREA)
TYPE задается как в операторе TLOAD1
T1,T2 временные константы (T2>T1)
F частота (Гц)
P фазовый угол (градусы)
C экспоненциальный коэффициенты
B показатель степени
Оператор TLOAD2 инициируется оператором DLOAD в Case Control Section.
Слайд 23
Комбинация нагрузок –
оператор DLOAD
Эффективное воздействие PC является суммой
различных компонентов нагрузки PK
где
SC – глобальный масштабный фактор
SK – масштабный фактор для k-го компонента
PK – идентификатор оператора TLOAD
Операторы TLOAD1 и TLOAD2 должны иметь уникальные идентификаторы.
Оператор DLOAD “объединяет” операторы TLOADi.
Оператор DLOAD в Bulk Data Section инициируется оператором DLOAD в Case Control Section.
Слайд 24
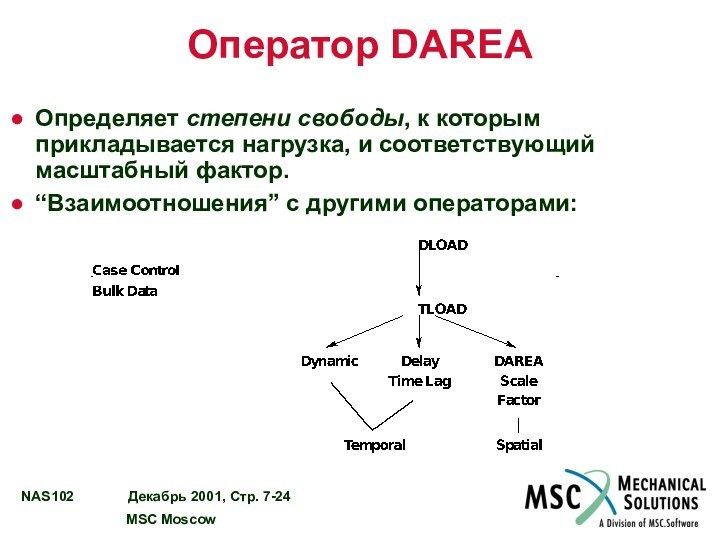
Оператор DAREA
Определяет степени свободы, к которым прикладывается нагрузка,
и соответствующий масштабный фактор.
“Взаимоотношения” с другими операторами:
Слайд 25
Пример оператора DAREA
DLOAD = 35
Результат: нагрузка, задаваемая оператором
TLOAD1, умножается на 5,2, “сдвигается” по времени (в сторону
запаздывания) на 0,2с и прикладывается к узлу 30 в направлении оси X (компонент T1).
Слайд 26
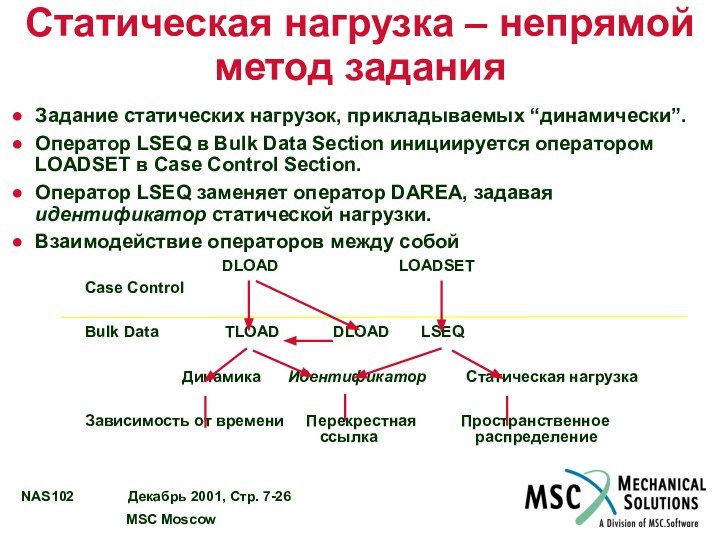
Статическая нагрузка – непрямой метод задания
Задание статических нагрузок,
прикладываемых “динамически”.
Оператор LSEQ в Bulk Data Section инициируется оператором
LOADSET в Case Control Section.
Оператор LSEQ заменяет оператор DAREA, задавая идентификатор статической нагрузки.
Взаимодействие операторов между собой
DLOAD LOADSET
Case Control
Bulk Data TLOAD DLOAD LSEQ
Динамика Идентификатор Статическая нагрузка
Зависимость от времени Перекрестная Пространственное
ссылка распределение
Слайд 27
Статическая нагрузка – непрямой метод задания
DLOAD
= 25
LOADSET = 27
TLOAD1 25 28
LSEQ 27 28 100
PLOAD4 100 ….
Слайд 28
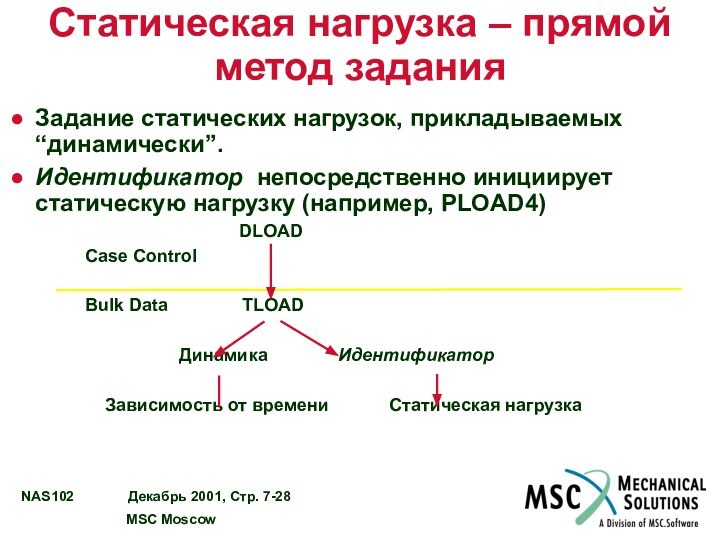
Статическая нагрузка – прямой метод задания
Задание статических нагрузок,
прикладываемых “динамически”.
Идентификатор непосредственно инициирует статическую нагрузку (например, PLOAD4)
DLOAD
Case Control
Bulk Data TLOAD
Динамика Идентификатор
Зависимость от времени Статическая нагрузка
Слайд 29
Статическая нагрузка – прямой метод задания
DLOAD = 25
TLOAD1 25 100
PLOAD4 100 …..
Слайд 30
Замечания к способу задания внешнего воздействия
Учитывайте осреднение нагрузок
(1/3). Это сделает нагрузки более плавными и уменьшит влияние
погрешностей.
Избегайте “разрывов” в нагрузках. Это может приводить к различиям в результатам расчетов, выполняемых на разных ЭВМ.
Если N·Δt = t(ABC), тогда MSC.Nastran вычислит: Force = (A+C)/2 = B.
Однако, вследствие ошибок округления, на одной ЭВМ N·Δt = t(A-) и тогда Force = A. На другой ЭВМ может быть N·Δt = t(C+) и тогда Force = C.
Результаты интегрирования будут различными в зависимости от того, чему равно N·Δt: A, B или C.
Слайд 31
Замечания к способу задания внешнего воздействия
Сгладьте разрыв в
силе на участке в один шаг Δt.
Слайд 32
Начальные условия
Начальные значения перемещений и/или скоростей можно учесть
при использовании прямого метода анализа переходного процесса с помощью
оператора TIC в Bulk Data Section. В стандартном модальном методе анализа учесть ненулевые начальные условия нельзя.
Оператор TIC инициируется оператором IC в Case Control Section.
Внимание: если начальные условия не указаны – они нулевые.
Начальные условия можно задать только для СС, входящих в A-set.
Значения {u0}, {u-1}, {P0} и {P-1}, необходимые для вычисления {u1}, определяются с использованием начальных условий, при этом ускорения при t < 0 полагаются равными нулю (скорости постоянны).
Нагрузка, заданная пользователем для t = 0, заменяется значением:
Слайд 33
Начальные условия
Практическая рекомендация: при любом типе динамического воздействия,
по-возможности, предусматривать хотя бы один шаг решения с “нулевой”
нагрузкой (до того, как ее величина примет действительное значение).
Слайд 35
Оператор TSTEP
Задает шаг интегрирования для прямого и модального
методов анализа.
Ошибки интегрирования растут с ростом собственных частот.
Рекомендуется, чтобы
на периоде самой высокочастотной составляющей отклика укладывалось не меньше восьми шагов Δt.
Оператор TSTEP в Bulk Data Section, задающий шаги решения и вывода результатов, инициируется оператором TSTEP в Case Control Section.
Если Δt постоянен, то затраты на интегрирование прямо пропорциональны количеству шагов по времени.
Необходимо задавать длительность моделирования достаточную для исследования низкочастотных составляющих отклика.
Пользователь может изменить шаг. Предполагается постоянство при t < NΔt1 . На базе вычисляются новые начальные условия для продолжения интегрирования начиная с {un}. Допущение постоянства ускорений обеспечивает плавность интегрирования в “переходной” зоне.
Слайд 36
Оператор TSTEP
Начальные условия для нового этапа интегрирования:
Примечание: необходимо
снова вычислить матрицы A1 - A4 (см. стр. 7-7),
а матрицу A1 - еще и обратить.
Слайд 38
Предусмотрены три метода вычисления перемещений и напряжений в

модальном анализе: модальных перемещений, матричный и модальных ускорений.
В методе
модальных перемещений по ним вычисляются физические перемещения, а затем - определяются напряжения. Количество операций пропорционально количеству шагов по времени (T).
В матричном методе вычисляются физические перемещения и напряжения в элементах для каждой моды, а затем вычисляются суммарные перемещения и напряжения как суммы этих величин по всем модам. Вычислительные затраты пропорциональны количеству мод (H).
Поскольку обычно H << T, матричный метод “дешевле”.
Матричный метод задан “по умолчанию” и рекомендуется для большинства случаев. Метод модальных перемещений может быть инициирован с помощью параметра PARAM, DDRMM, -1.
Метод модальных ускорений автоматически задействуется при вычислении квазистатического отклика всех высокочастотных мод (требуется также “подключение” метода модальных перемещений, подробнее - см. Приложение F).
Методы вычисления результатов
Слайд 39
Применение модального и прямого методов анализа
Слайд 40
Управление решением при анализе переходного процесса
Executive Control Section
SOL
Case Control Section
DLOAD (требуется при обоих методах решения)
LOADSET (может применяться
при обоих методах)
METHOD (требуется при модальном методе)
SDAMPING (может применяться при модальном методе)
IC (может применяться при прямом методе)
TSTEP (требуется при обоих методах решения)
Слайд 41
Управление решением при анализе переходного процесса
Bulk Data Section
ASET,OMIT (может
применяться при обоих методах)
EIGRL or EIGR (требуется при модальном методе)
TSTEP (требуется
при обоих методах решения)
TIC (может применяться при прямом методе)
TLOADi (требуется при обоих методах решения)
LSEQ (может применяться при обоих методах)
TABLEDi (может применяться при обоих методах)
DAREA (требуется при обоих методах решения*)
DELAY (может применяться при обоих методах)
DLOAD (может применяться при обоих методах)
TABDMP1 (может применяться при модальном методе)
*Идентификатор оператора DAREA необходим; если же применяется оператор LSEQ, то сам оператор DAREA может отсутствовать.
Слайд 42
Виды вычисляемых величин
Результаты вычислений для узлов
ACCELERATION
DISPLACEMENT (или VECTOR)
GPSTRESS
NLLOAD
(вывод значений нелинейных нагрузок)
OLOAD (вывод значений прилагаемых нагрузок)
SACCELERATION
(вывод результатов решения для A-set
SDISPLACEMENT при прямом методе анализа, для модальных
SVELOCITY переменных – при модальном методе анализа)
SVECTOR (вывод результатов вычислений собственных форм для A-set)
SPCFORCES
VELOCITY
MPCFORCE
Результаты вычислений для элементов
ELSTRESS (или STRESS)
ELFORCE (или FORCE)
STRAIN
Специальный оператор
OTIME (задание моментов времени, в которые должны выводиться результаты;
работает совместно с оператором TSTEP)
Слайд 43
Пример №3
Анализ переходного процесса прямым методом
Слайд 44
Пример №3. Анализ переходного процесса прямым методом
Используя модель
из Примера №1, прямым методом определите колебания плоской пластины
под действием возмущения, зависящего от времени. Конструкция нагружается давлением 1 фунт/кв. дюйм, изменяющимся с f=250 Гц, а также силой в 50 фунтов, приложенной к углу пластины и изменяющейся с f=250 Гц и сдвинутой по фазе на 180o относительно давления. Длительность действия обоих возмущений -0,008 с. Конструкционное демпфирование g=0,06. Указанное демпфирование конвертировать в вязкое на частоте 250 Гц. Длительность процесса 0,04 с.
Рис. 7-1. Нагрузки и граничные условия.
Слайд 45
Входной файл для Примера №3
ID SEMINAR, PROB3
SOL 109
TIME

30
CEND
TITLE= TRANSIENT RESOPONSE WITH TIME DEPENDENT PRESSURE AND POINT
LOADS
SUBTITLE= USE THE DIRECT METHOD
ECHO= PUNCH
SPC= 1
SET 1= 11, 33, 55
DISPLACEMENT= 1
SUBCASE 1
DLOAD= 700 $ SELECT TEMPORAL COMPONENT OF TRANSIENT LOADING
LOADSET= 100 $ SELECT SPACIAL DISTRIBUTION OF TRANSIENT LOADING
TSTEP= 100 $ SELECT INTERGRATION TIME STEPS
$
OUTPUT (XYPLOT)
XGRID=YES
YGRID=YES
XTITLE = TIME (SEC)
YTITLE- DISPLACEMENT RESPONSE AT CENTER TIP
XYPLOT DISP RESONSE / 11(T3)
YTITLE= DISPLACEMENT RESPONSE AT CENTER TIP
XYPLOT DISP RESPONSE / 33 (T3)
YTITLE= DISPLACEMENT RESPONSE AT OPPSITE CORNER
XYPLOT DISP RESPONSE / 55 (T3)
$
BEGIN BULK
PARAM, COUPMASS, 1
PARAM, WTMASS, 0.00259
$
INCLUDE ’plate.bdf’
$
$ SPECIFY STRUCTURAL DIAMPING
$ 3 PERCENT AT 250 HZ. = 1571 RAD/SEC
$
PARAM, G, 0.06
PARAM, W3, 1571.
$
$ APPLY UNTI PRESSURE LOAD TO PLATE
$
LSEQ, 100, 300, 400
$
PLOAD2, 400, 1., 1, THRU, 40
$
$ VARY PRESSURE LOAD (250HZ)
$
TLOAD2, 200, 300, , 0, 0., 8.E-3, 250., -90.
$
$ APPLY POINT LOAD OUT OF PAHSE WITH PRESSURE LOAD
$
TLOAD2, 500, 600, , 0, 0., 8.E-3, 250., 90.
$
DAREA, 600, 11, 3, 1.
$
$ COMBINE LOADS
$
DLOAD, 700, 1., 1., 200, 50., 500
$
$ SPECIFY INTERGRATION TIME STEPS
$
TSTEP, 100, 100, 4.0E-4, 1
$
ENDDATA
Слайд 46
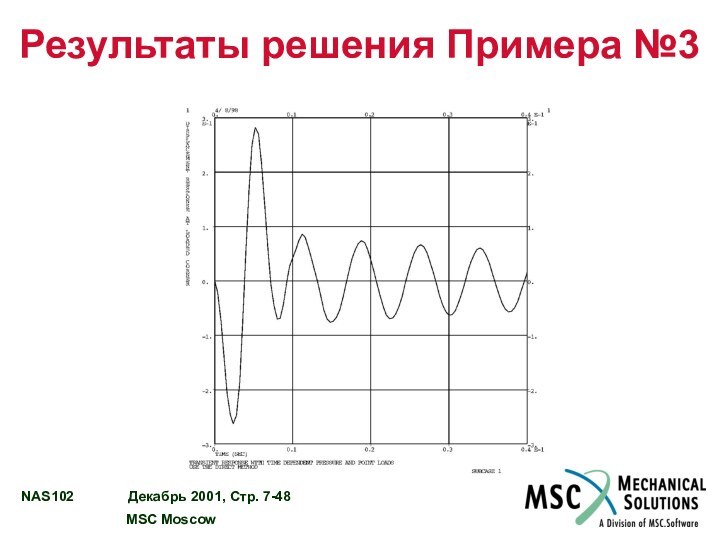
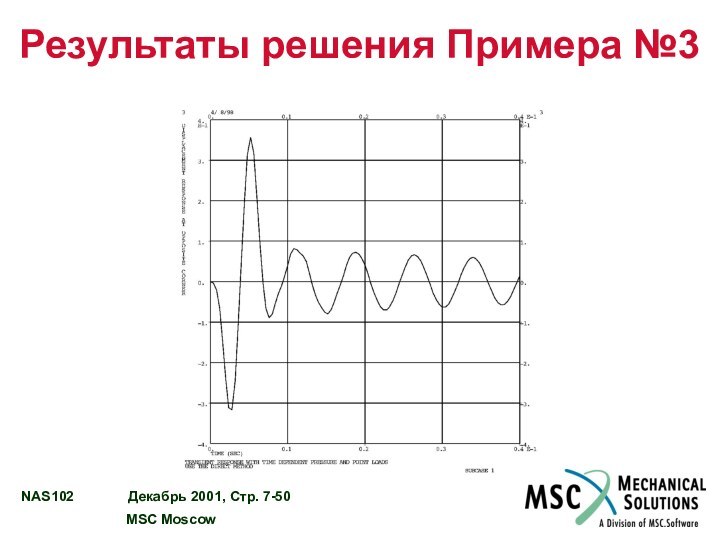
Результаты решения Примера №3
0

SUBCASE 1ML
POINT-ID = 11
D I S P L A C E M E N T V E C T O R
TIME TYPE T1 T2 T3 R1 R2 R3
.0 G .0 .0 .0 .0 .0 .0
4.000000E-04 G .0 .0 -2.173625E-02 1.104167E-02 1.050818E-02 .0
8.000000E-04 G .0 .0 -7.204904E-02 2.847414E-02 2.852519E-02 .0
1.200000E-03 G .0 .0 -1.433462E-01 4.082027E-02 4.915178E-02 .0
.
.
.
3.999996E-02 G .0 .0 1.535974E-02 5.380195E-06 -4.281028E-03 .0
.
.
.
.
.
.
POINT-ID = 33
D I S P L A C E M E N T V E C T O R
TIME TYPE T1 T2 T3 R1 R2 R3
.0 G .0 .0 .0 .0 .0 .0
4.000000E-04 G .0 .0 -1.122398E-02 9.220219E-03 6.138594E-03 .0
8.000000E-04 G .0 .0 -4.424753E-02 2.576699E-02 2.014980E-02 .0
1.200000E-03 G .0 .0 -1.030773E-01 3.819037E-02 3.922388E-02 .0
1.600000E-03 G .0 .0 -1.756290E-01 2.927664E-02 5.577566E-02 .0
2.000000E-03 G .0 .0 -2.443317E-01 1.765907E-03 6.761354E-02 .0
.
.
.
3.839996E-02 G .0 .0 -4.946285E-02 -3.005945E-05 1.376158E-02 .0
3.879996E-02 G .0 .0 -3.729695E-02 1.898671E-05 1.037927E-02 .0
3.919996E-02 G .0 .0 -2.121863E-02 3.488552E-05 5.907703E-03 .0
3.959996E-02 G .0 .0 -3.002587E-03 -2.227573E-07 8.361285E-04 .0
3.999996E-02 G .0 .0 1.535096E-02 -3.032754E-05 -4.274250E-03 .0
Слайд 47
Результаты решения Примера №3
0

1 TRANSIENT RESPONSE WITH TIME DEPENDENT PRESSURE AND POINT LOADS APRIL 8, 1998 MSC.Nastran 4/ 6/98 PAGE 16
USE THE DIRECT METHOD
0 SUBCASE 1
0 X Y - O U T P U T S U M M A R Y ( R E S P O N S E )
0 SUBCASE CURVE FRAME XMIN-FRAME/ XMAX-FRAME/ YMIN-FRAME/ X FOR YMAX-FRAME/ X FOR
ID TYPE NO. CURVE ID. ALL DATA ALL DATA ALL DATA YMIN ALL DATA YMAX
0 1 DISP 1 11( 5) 0.000000E+00 3.999996E-02 -2.623279E-01 2.400000E-03 2.823930E-01 5.199999E-03
0.000000E+00 3.999996E-02 -2.623279E-01 2.400000E-03 2.823930E-01 5.199999E-03
0 1 DISP 2 33( 5) 0.000000E+00 3.999996E-02 -2.882706E-01 2.400000E-03 3.220944E-01 5.199999E-03
0.000000E+00 3.999996E-02 -2.882706E-01 2.400000E-03 3.220944E-01 5.199999E-03
0 1 DISP 3 55( 5) 0.000000E+00 3.999996E-02 -3.165697E-01 2.800000E-03 3.570921E-01 5.199999E-03
0.000000E+00 3.999996E-02 -3.165697E-01 2.800000E-03 3.570921E-01 5.199999E-03
1 TRANSIENT RESPONSE WITH TIME DEPENDENT PRESSURE AND POINT LOADS APRIL 8, 1998 MSC.Nastran 4/ 6/98 PAGE 17
USE THE DIRECT METHOD
0
* * * * D B D I C T P R I N T * * * * SUBDMAP = PRTSUM , DMAP STATEMENT NO. 13
0 * * * * A N A L Y S I S S U M M A R Y T A B L E * * * *
0 SEID PEID PROJ VERS APRCH SEMG SEMR SEKR SELG SELR MODES DYNRED SOLLIN PVALID SOLNL LOOPID DESIGN CYCLE SENSITIVITY
--------------------------------------------------------------------------------------------------------------------------
0 0 1 1 ’ ’ T T T T T F F T 0 F -1 0 F
0SEID = SUPERELEMENT ID.
PEID = PRIMARY SUPERELEMENT ID OF IMAGE SUPERELEMENT.
PROJ = PROJECT ID NUMBER.
VERS = VERSION ID.
APRCH = BLANK FOR STRUCTURAL ANALYSIS. HEAT FOR HEAT TRANSFER ANALYSIS.
SEMG = STIFFNESS AND MASS MATRIX GENERATION STEP.
SEMR = MASS MATRIX REDUCTION STEP (INCLUDES EIGENVALUE SOLUTION FOR MODES).
SEKR = STIFFNESS MATRIX REDUCTION STEP.
SELG = LOAD MATRIX GENERATION STEP.
SELR = LOAD MATRIX REDUCTION STEP.
MODES = T (TRUE) IF NORMAL MODES OR BUCKLING MODES CALCULATED.
DYNRED = T (TRUE) MEANS GENERALIZED DYNAMIC AND/OR COMPONENT MODE REDUCTION PERFORMED.
SOLLIN = T (TRUE) IF LINEAR SOLUTION EXISTS IN DATABASE.
PVALID = P-DISTRIBUTION ID OF P-VALUE FOR P-ELEMENTS
LOOPID = THE LAST LOOPID VALUE USED IN THE NONLINEAR ANALYSIS. USEFUL FOR RESTARTS.
SOLNL = T (TRUE) IF NONLINEAR SOLUTION EXISTS IN DATABASE.
DESIGN CYCLE = THE LAST DESIGN CYCLE (ONLY VALID IN OPTIMIZATION).
SENSITIVITY = SENSITIVITY MATRIX GENERATION FLAG.
1 * * * END OF JOB * * *
Слайд 51
Пример №4
Анализ переходного процесса модальным методом
Слайд 52
Пример №4. Анализ переходного процесса модальным методом
Используя модель
из Примера №1, модальным методом определите колебания плоской пластины
под действием возмущения, зависящего от времени. Конструкция нагружается давлением 1 фунт/кв. дюйм, изменяющимся с f=250 Гц, а также силой в 25 фунтов, приложенной к углу пластины и изменяющейся с f=250 Гц. Сила прикладывается начиная с 0,004 с. Действие обоих возмущений заканчивается через 0,008 с. Модальное демпфирование ζ=0,06 для всех мод. Длительность процесса 0,04 с.
Слайд 53
Входной файл для Примера №4
ID SEMINAR, PROB4
SOL 112
TIME
30
CEND
TITLE = TRANSIENT RESPONSE WITH TIME DEPENDENT PRESSURE AND
POINT LOADS
SUBTITLE = USE THE MODAL METHOD
ECHO = UNSORTED
SPC = 1
SET 111 = 11, 33, 55
DISPLACEMENT(SORT2) = 111
SDAMPING = 100
SUBCASE 1
METHOD = 100
DLOAD = 700
LOADSET = 100
TSTEP = 100
$
OUTPUT (XYPLOT)
XGRID=YES
YGRID=YES
XTITLE= TIME (SEC)
YTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER
XYPLOT DISP RESPONSE / 11 (T3)
YTITLE= DISPLACEMENT RESPONSE AT TIP CENTER
XYPLOT DISP RESPONSE / 33 (T3)
YTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER
XYPLOT DISP RESPONSE / 55 (T3)
$
BEGIN BULK
PARAM, COUPMASS, 1
PARAM, WTMASS, 0.00259
$
$ PLATE MODEL DESCRIBED IN NORMAL MODES EXAMPLE PROBLEM
$
INCLUDE ’plate.bdf’
$
$ EIGENVALUE EXTRACTION PARAMETERS
$
EIGRL, 100, , ,5
$
$ SPECIFY MODAL DAMPING
$
TABDMP1, 100, CRIT,
+, 0., .03, 10., .03, ENDT
$
$ APPLY UNIT PRESSURE LOAD TO PLATE
$
LSEQ, 100, 300, 400
$
Слайд 54
Входной файл для Примера №4
PLOAD2, 400, 1., 1,
THRU, 40
$
$ VARY PRESSURE LOAD (250 HZ)
$
TLOAD2, 200, 300,
, 0, 0., 8.E-3, 250., -90.
$
$ APPLY POINT LOAD (250 HZ)
$
TLOAD2, 500, 600,610, 0, 0.0, 8.E-3, 250., -90.
$
DAREA, 600, 11, 3, 1.
DELAY, 610, 11, 3, 0.004
$
$ COMBINE LOADS
$
DLOAD, 700, 1., 1., 200, 25., 500
$
$ SPECIFY INTERGRATION TIME STEPS
$
TSTEP, 100, 100, 4.0E-4, 1
$
ENDDATA
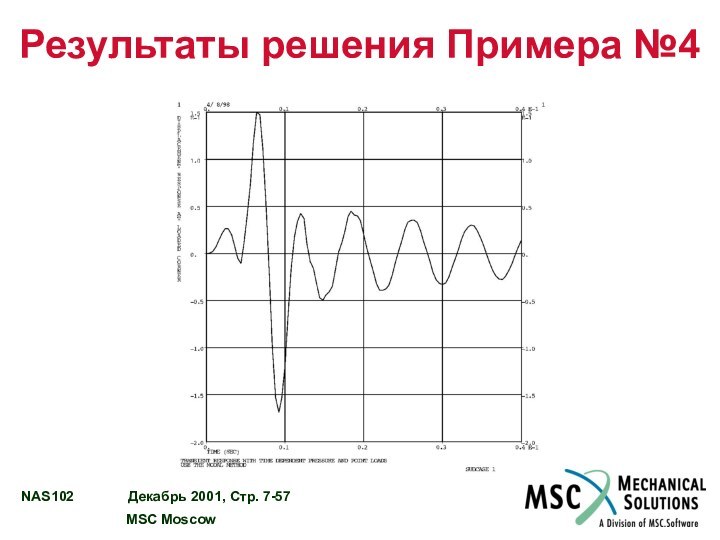
Слайд 55
Результаты решения Примера №4
*** SYSTEM INFORMATION MESSAGE

6916 (DFMSYN)
DECOMP ORDERING METHOD CHOSEN: DEFAULT,
ORDERING METHOD USED: MMD
*** USER INFORMATION MESSAGE 5010 (LNCILD)
STURM SEQUENCE DATA FOR EIGENVALUE EXTRACTION.
TRIAL EIGENVALUE = 9.433958D+07, CYCLES = 1.545849D+03 NUMBER OF EIGENVALUES BELOW THIS VALUE = 3
*** USER INFORMATION MESSAGE 5010 (LNCILD)
STURM SEQUENCE DATA FOR EIGENVALUE EXTRACTION.
TRIAL EIGENVALUE = 2.281618D+08, CYCLES = 2.404039D+03 NUMBER OF EIGENVALUES BELOW THIS VALUE = 5
TABLE OF SHIFTS: (LNNRIGL)
SHIFT # SHIFT VALUE FREQUENCY, CYCLES # EIGENVALUES BELOW # NEW EIGENVALUES FOUND
1. 9.4339576E+07 1.5458490E+03 3 6
2. 2.2816176E+08 2.4040393E+03 5 0
1 TRANSIENT RESPONSE WITH TIME DEPENDENT PRESSURE AND POINT LOADS APRIL 8, 1998 MSC.Nastran 4/ 6/98 PAGE 10
USE THE MODAL METHOD
0
0
E I G E N V A L U E A N A L Y S I S S U M M A R Y (READ MODULE)
BLOCK SIZE USED ...................... 7
NUMBER OF DECOMPOSITIONS ............. 2
NUMBER OF ROOTS FOUND ................ 5
NUMBER OF SOLVES REQUIRED ............ 5
1 TRANSIENT RESPONSE WITH TIME DEPENDENT PRESSURE AND POINT LOADS APRIL 8, 1998 MSC.Nastran 4/ 6/98 PAGE 11
USE THE MODAL METHOD
0
R E A L E I G E N V A L U E S
MODE EXTRACTION EIGENVALUE RADIANS CYCLES GENERALIZED GENERALIZED
NO. ORDER MASS STIFFNESS
1 1 7.056994E+05 8.400591E+02 1.336996E+02 1.000000E+00 7.056994E+05
2 2 1.878432E+07 4.334088E+03 6.897916E+02 1.000000E+00 1.878432E+07
3 3 2.811467E+07 5.302327E+03 8.438915E+02 1.000000E+00 2.811467E+07
4 4 1.931709E+08 1.389859E+04 2.212030E+03 1.000000E+00 1.931709E+08
5 5 2.234434E+08 1.494802E+04 2.379052E+03 1.000000E+00 2.234434E+08
Слайд 56
Результаты решения Примера №4
POINT-ID =

11
D I S P L A C E M E N T V E C T O R
TIME TYPE T1 T2 T3 R1 R2 R3
.0 G .0 .0 .0 .0 .0 .0
4.000000E-04 G -3.625017E-15 -1.905611E-15 1.887243E-04 -6.386437E-06 5.199215E-05 .0
8.000000E-04 G -2.914862E-14 -1.814328E-14 1.956669E-03 -2.026748E-05 -1.663007E-04 .0
1.200000E-03 G -8.908526E-14 -5.652777E-14 6.887082E-03 -4.435436E-06 -1.612398E-03 .0
.
.
.
3.919996E-02 G 2.885643E-14 1.851072E-14 -2.561149E-03 1.920348E-04 6.726292E-04 .0
3.959996E-02 G -7.876552E-14 -5.047815E-14 6.422142E-03 -1.141607E-05 -1.799371E-03 .0
3.999996E-02 G -1.754870E-13 -1.124985E-13 1.438590E-02 -1.381519E-04 -3.964385E-03 .0
.
.
.
.
.
.
POINT-ID = 33
D I S P L A C E M E N T V E C T O R
TIME TYPE T1 T2 T3 R1 R2 R3
.0 G .0 .0 .0 .0 .0 .0
4.000000E-04 G -2.425735E-15 -3.601817E-15 1.849105E-04 1.747102E-13 5.123477E-05 .0
8.000000E-04 G -1.846279E-14 -3.116278E-14 1.944596E-03 1.289274E-12 -1.686260E-04 .0
.
.
.
3.839996E-02 G 1.418105E-13 2.481614E-13 -1.858122E-02 -2.107761E-04 5.154297E-03 .0
3.879996E-02 G 8.371286E-14 1.466735E-13 -1.103474E-02 -3.810626E-05 3.082996E-03 .0
3.919996E-02 G 1.725147E-14 3.062306E-14 -2.364378E-03 2.016205E-04 6.607183E-04 .0
3.959996E-02 G -4.836024E-14 -8.483060E-14 6.404299E-03 -2.743191E-05 -1.795630E-03 .0
3.999996E-02 G -1.075141E-13 -1.887765E-13 1.423312E-02 -1.733039E-04 -3.950206E-03 .0
.
.
.
0 SUBCASE 1
0 X Y - O U T P U T S U M M A R Y ( R E S P O N S E )
0 SUBCASE CURVE FRAME XMIN-FRAME/ XMAX-FRAME/ YMIN-FRAME/ X FOR YMAX-FRAME/ X FOR
ID TYPE NO. CURVE ID. ALL DATA ALL DATA ALL DATA YMIN ALL DATA YMAX
0 1 DISP 1 11( 5) 0.000000E+00 3.999996E-02 -1.690216E-01 9.199998E-03 1.497643E-01 6.399998E-03
0.000000E+00 3.999996E-02 -1.690216E-01 9.199998E-03 1.497643E-01 6.399998E-03
0 1 DISP 2 33( 5) 0.000000E+00 3.999996E-02 -1.849363E-01 9.199998E-03 1.606161E-01 6.799998E-03
0.000000E+00 3.999996E-02 -1.849363E-01 9.199998E-03 1.606161E-01 6.799998E-03
0 1 DISP 3 55( 5) 0.000000E+00 3.999996E-02 -2.005836E-01 9.199998E-03 1.734470E-01 6.799998E-03
0.000000E+00 3.999996E-02 -2.005836E-01 9.199998E-03 1.734470E-01 6.799998E-03