Слайд 2
Раздел 12. Вынужденное перемещение
ВЫНУЖДЕННОЕ ПЕРЕМЕЩЕНИЕ В ДИНАМИЧЕСКОМ АНАЛИЗЕ………………12

- 4
МЕТОДЫ АНАЛИЗА………………......................................................………............ 12 - 5
МЕТОД №1...…………...…………………………………………………………………... 12 -
6
НАБОРЫ СТЕПЕНЕЙ СВОБОДЫ………........................................................……. 12 - 7
ОСНОВНЫЕ УРАВНЕНИЯ……..………............………………………….................... 12 - 8
УРАВНЕНИЯ ДЛЯ АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ…………………….... 12 - 9
УРАВНЕНИЯ ДЛЯ АНАЛИЗА ЧАСТОТНОГО ОТКЛИКА…..……………………….. 12 - 10
ЗАМЕЧАНИЕ К МОДАЛЬНОМУ МЕТОДУ...........................................……………... 12 - 11
ИНТЕРФЕЙС ПОЛЬЗОВАТЕЛЯ...…….............................................……………….... 12 - 12
ПАРАМЕТР TYPE……….……………….............................……………………………... 12 - 13
ПРИМЕР: РАЗДЕЛЫ EXECUTIVE И CASE CONTROL……………………………….. 12 - 14
ПРИМЕР: РАЗДЕЛ BULK DATA…………............................................………………. 12 - 15
ПРИМЕР №7A – ПРЯМОЙ АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА С
ВЫНУЖДЕННЫМ ПЕРЕМЕЩЕНИЕМ.……………….…...........………………………. 12 - 16
Слайд 3
Вынужденное перемещение (продолж.)
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №7A…………………..............……………………12 -
18
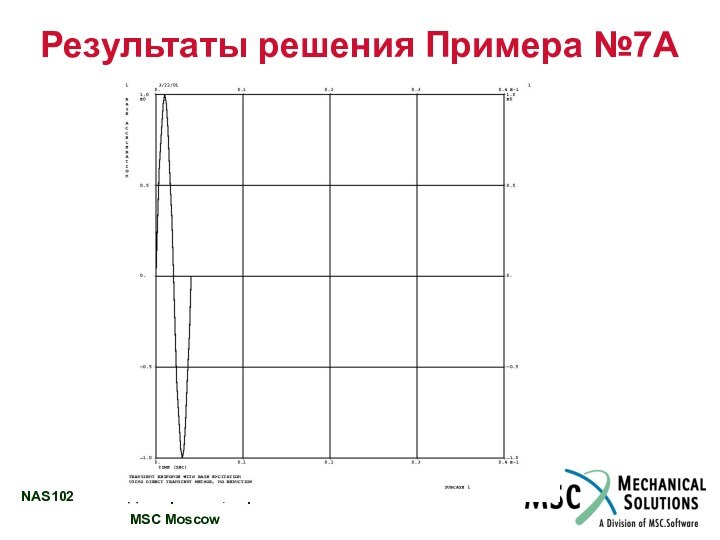
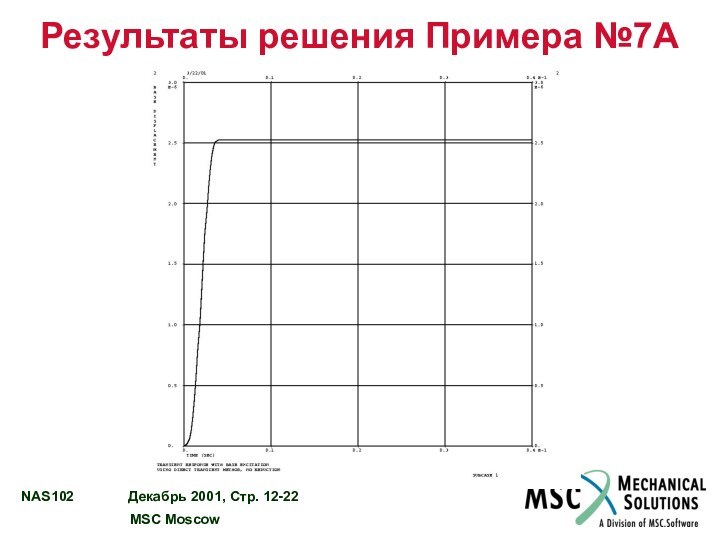
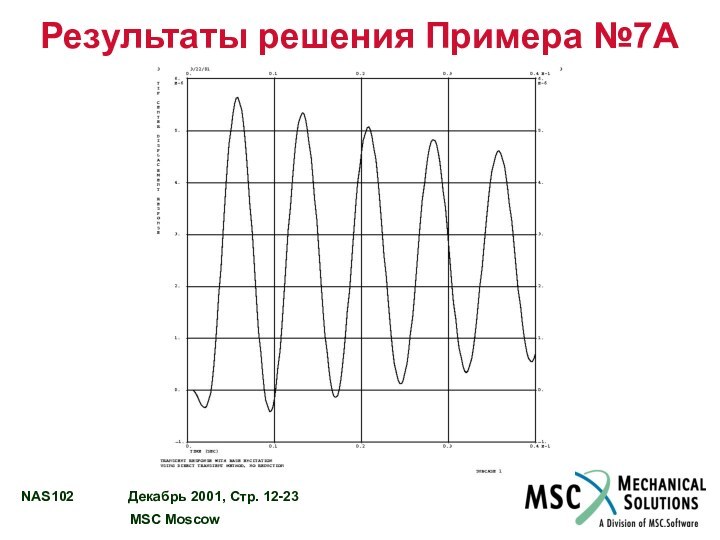
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №7A………………………...……................... 12 – 20
ПРИМЕР №8B –
МОДАЛЬНЫЙ АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА С
ВЫНУЖДЕННЫМ ПЕРЕМЕЩЕНИЕМ………………………………………………….. 12 - 24
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №7B…………………..................................…... 12 - 26
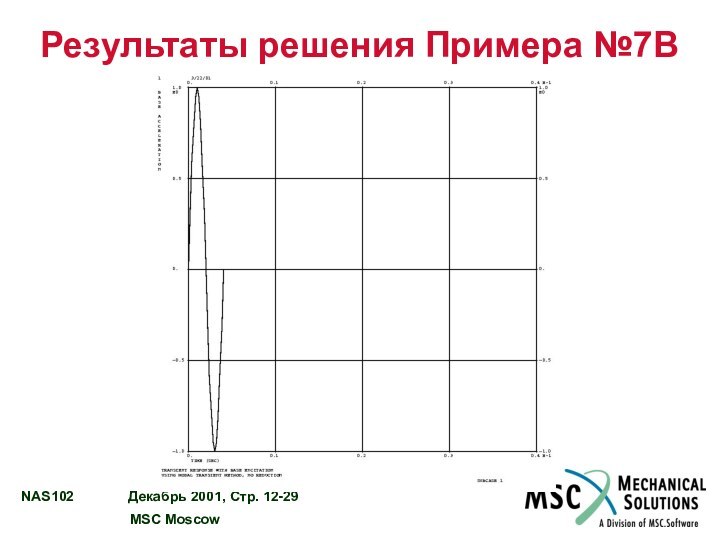
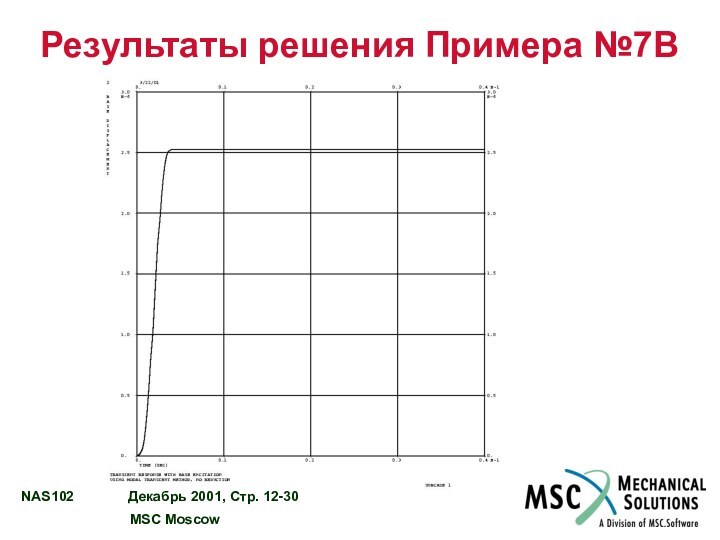
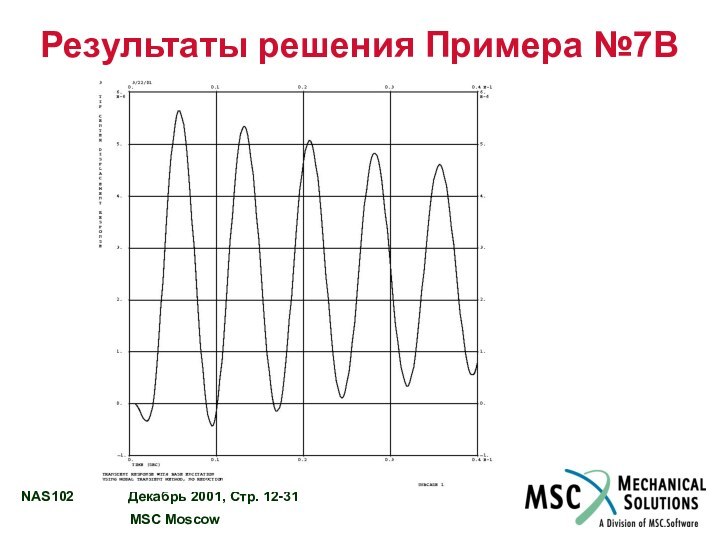
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №7B……………………….....................….…12 - 28
ПРИМЕР №8A – ПРЯМОЙ АНАЛИЗ ЧАСТОТНОГО ОТКЛИКА С
ВЫНУЖДЕННЫМ ПЕРЕМЕЩЕНИЕМ………………………………….….…...…….. 12 - 32
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №8A...……………………................................ 12 - 34
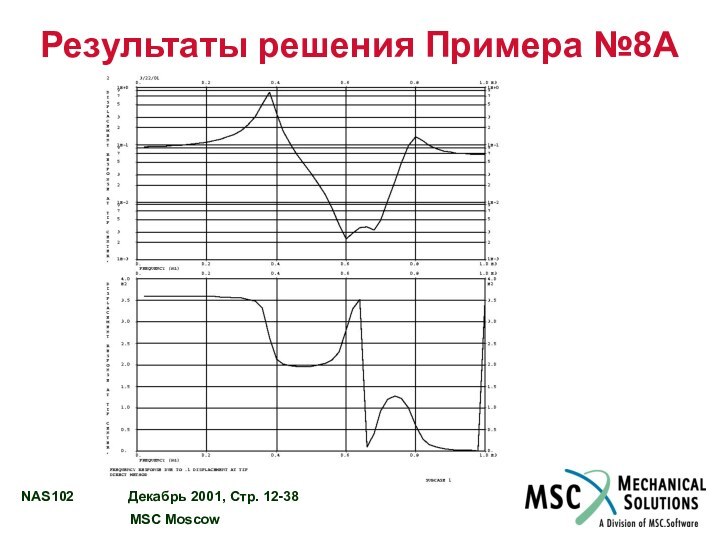
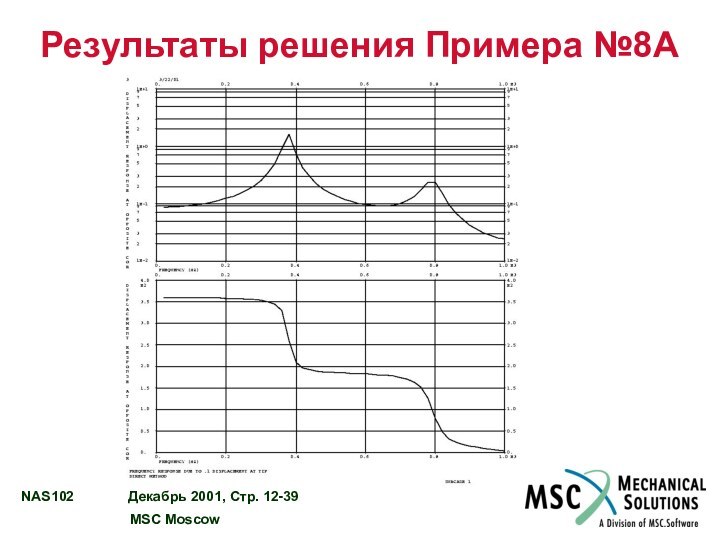
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №8A………………...…….......................... 12 - 36
ПРИМЕР №8B - МОДАЛЬНЫЙ АНАЛИЗ ЧАСТОТНОГО ОТКЛИКА С
ВЫНУЖДЕННЫМ ПЕРЕМЕЩЕНИЕМ………………………………….….…...……. 12 - 40
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №8B......……………………............................ 12 - 42
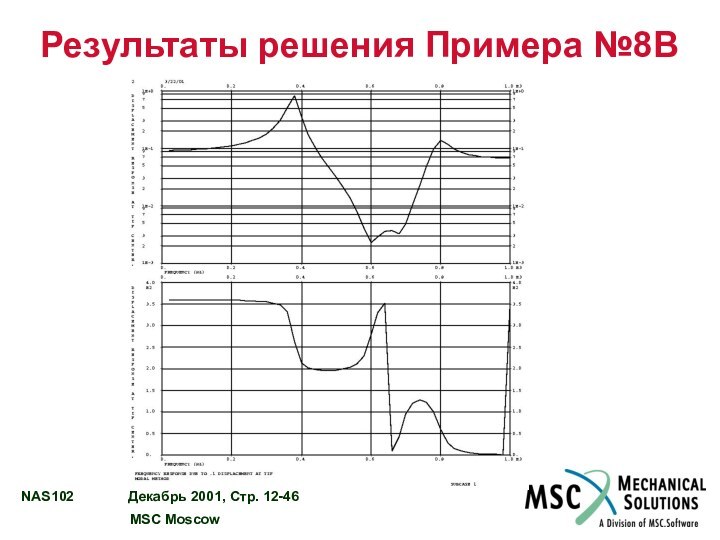
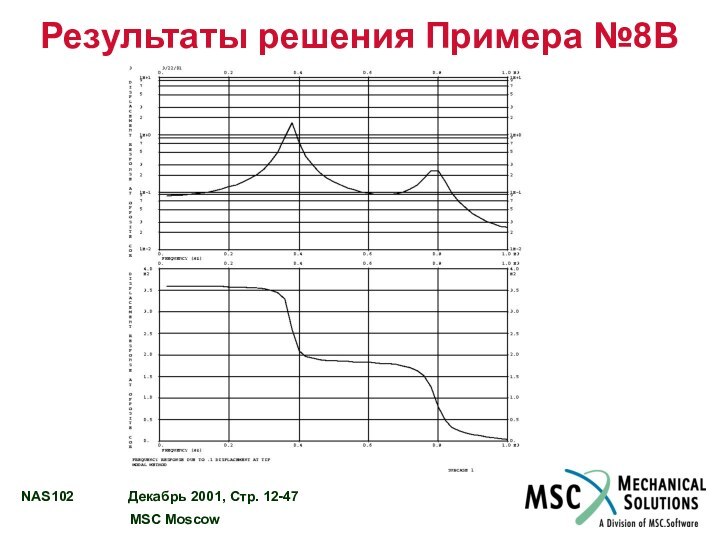
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №8A………………………......................... 12 - 44
Слайд 4
Вынужденное перемещение в динамическом анализе
Используется для анализа конструкций,
подверженных заданным перемещениям, скоростям и ускорениям.
Примеры воздействий: землетрясение (для
анализа переходного процесса), вибрационный стенд с качающейся частотой (для анализа частотного отклика), дорожное воздействие на подвеску колес автомобиля.
Слайд 5
Методы анализа
Предусмотрено четыре метода:
1. Прямое задание вынужденного перемещения,
скорости или
ускорения (рекомендуемый метод).
2. Метод
большой массы (см. Приложение E)
3. Метод большой жесткости (только вынужденное перемещение,
см. Приложение E)
4. Метод множителей Лагранжа (см. Приложение E)
Слайд 6
Метод №1
Метод №1 – рекомендуемый метод и он
обсуждается на данном семинаре.
Этот метод предусмотрен в MSC.Nastran
(версия 2001 и дальнейших).
В данном методе вынужденное перемещение моделируется прямым заданием необходимых перемещения, скорости или ускорения с помощью операторов SPC / SPC1 и SPCD в Bulk Data Section.
Интерфейс метода очень близок к интерфейсу вынужденного перемещения в статическом анализе.
Слайд 7
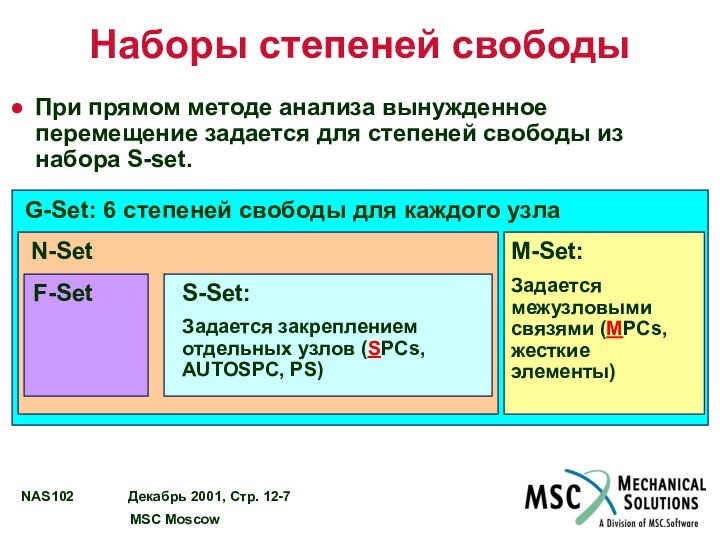
Наборы степеней свободы
При прямом методе анализа вынужденное перемещение
задается для степеней свободы из набора S-set.
Слайд 8
Основные уравнения
Для набора N-set уравнения колебаний выглядят как
где
⎭
⎬
⎫
⎩
⎨
⎧
+
=
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
+
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
+
⎭
⎬
⎫
⎩
⎨
⎧
⎥
⎦
⎤
⎢
⎣
⎡
s
q
p
p
u
u
K
K
K
K
u
u
B
B
B
B
u
u
M
M
M
M
s
f
s
f
ss
sf
fs
ff
s
f
ss
sf
fs
ff
s
f
ss
sf
fs
ff
..
..
.
.
Слайд 9
Уравнения для анализа переходных процессов
Первое матричное уравнение может
быть решено относительно перемещений F-set:
Затем из второго матричного уравнения
определяются силы закреплений:
(
)
s
fs
s
fs
s
fs
f
f
ff
f
ff
f
ff
u
K
u
B
u
M
p
u
K
u
B
u
M
+
+
−
=
+
+
[
]
[
]
[
]
⎭
⎬
⎫
+
⎭
⎬
⎫
+
⎭
⎬
⎫
⎩
⎨
⎧
+
−
=
s
f
ss
sf
s
f
ss
sf
s
f
ss
sf
s
s
u
u
K
K
u
u
B
B
u
u
M
M
p
q
..
..
..
..
.
.
.
.
Слайд 10
Уравнения для анализа частотного отклика
При анализе частотного отклика
перемещения F-set определяются как
Силы закреплений определяются из следующего выражения
Слайд 11
Замечание к модальному методу
Основываясь на опыте, можно рекомендовать
всегда включать остаточные векторы в модальное решение.
В настоящее время
остаточные векторы по умолчанию в модальное решение не включаются.
Слайд 12
Интерфейс пользователя
Операторы SPC / SPC1 в Bulk Data
Section используются для идентификации степеней свободы (СС), для которых
задается вынужденное перемещение. Эти операторы активизируются оператором SPC в Case Control Section.
Операторы SPCD в Bulk Data Section используются для задания вынужденных перемещений. Эти операторы инициируются с помощью параметра EXCITEID в операторах TLOADi или RLOADi в Bulk Data Section.
Параметр TYPE в операторах TLOADi или RLOADi в Bulk Data Section определяет тип вынужденного перемещения (собственно перемещение, скорость или ускорение).
Оператор PARAM, RESVEC, YES должен быть использован для инициализации метода остаточных векторов. (В будущих версиях MSC.Nastran предполагается инициировать этот метод по умолчанию.)
Слайд 13
Параметр TYPE
Тип воздействия задается в поле 5 оператора
TLOADi в Bulk Data Section или в поле 8
оператора RLOADi в Bulk Data Section:
При буквенном обозначении, для краткости, название типа воздействия можно сократить даже до одной буквы.
Слайд 14
Пример: разделы Executive и
Case Control
SOL 111
CEND
$
TITLE =Example
for Direct Enforced Motion
SUBTITLE=Modal Frequency Response Analysis
$
SPC
=1
METHOD =10
FREQUENCY=20
$
SET 1 = 1000,1001
ACCELERATION(SORT2,PRINT,PHAS)=1
$
SUBCASE 1
LABEL=Unit Acceleration in x-Direction
DLOAD=100
$
SUBCASE 2
LABEL=Unit Acceleration in y-Direction
DLOAD=200
$
Слайд 15
Пример: раздел Bulk Data
BEGIN BULK
$
PARAM, G, 0.02
$
2% Structural Damping
SPC1, 1, 3456, 1000 $ z-Displ. and Rotations are fixed
SPC1, 1, 12, 1000 $ x- and y-Accelerations are prescribed
$
$ Modal Reduction
EIGRL, 10,, 150. $ Modes up to 150Hz
PARAM, RESVEC, YES $ Static Mode Shapes
$
$ Base Motion Excitation
$
RLOAD1, 100, 1001,,, 10,, A $ Load of Subcase 1:
SPCD, 1001, 1000, 1, 1. $ Unit x-Acceleration
$
RLOAD1, 200, 1002,,, 10,, A $ Load of Subcase 2:
SPCD, 1002, 1000, 2, 1. $ Unit y-Acceleration
$
TABLED1, 10 $ Constant for all Frequencies
, 0., 1., 100., 1., ENDT
FREQ1, 20, 1., 1., 49 $ Frequency Range from 1Hz to 50Hz
$
INCLUDE 'tower.bdf' $ Structural Model
$
ENDDATA
Слайд 16
Пример №7A
Прямой анализ переходного процесса с вынужденным перемещением
Слайд 17
Пример №7A. Прямой анализ переходного процесса с вынужденным
перемещением
Используя прямой метод, выполнить анализ переходного процесса колебаний модели.
Задано единичное синусоидальное ускорение заделки с частотой 250 Гц в Z направлении. Использовать конструкционное демпфирование g = 0,06, конвертировать его в вязкое на частоте 250 Гц.
Слайд 18
Входной файл для Примера №7A
ID SEMINAR, PROB7A
SOL 109
TIME
30
CEND
TITLE = TRANSIENT RESPONSE WITH BASE EXCITATION
SUBTITLE = USING
DIRECT TRANSIENT METHOD, NO REDUCTION
ECHO = UNSORTED
SPC = 200
SET 111 = 23, 33
DISPLACEMENT (SORT2) = 111
VELOCITY (SORT2) = 111
ACCELERATION (SORT2) = 111
SUBCASE 1
DLOAD = 500
TSTEP = 100
$
OUTPUT (XYPLOT)
XGRID=YES
YGRID=YES
XTITLE= TIME (SEC)
YTITLE= BASE ACCELERATION
XYPLOT ACCELERATION RESPONSE / 23 (T3)
YTITLE= BASE DISPLACEMENT
XYPLOT DISP RESPONSE / 23 (T3)
YTITLE= TIP CENTER DISPLACEMENT RESPONSE
XYPLOT DISP RESPONSE / 33 (T3)
$
BEGIN BULK
$
$ PLATE MODEL DESCRIBED IN NORMAL MODES EXAMPLE
$
INCLUDE ’plate.bdf’
PARAM, COUPMASS, 1
PARAM, WTMASS, 0.00259
$
$ SPECIFY STRUCTURAL DAMPING
$
PARAM, G, 0.06
PARAM, W3, 1571.
$
$ APPLY EDGE CONSTRAINTS
$
SPC1, 200, 12456, 1, 12, 23, 34, 45
Слайд 19
Входной файл для Примера №7A
$
$ APPLY ACCELERATION TO
THE BASE
$
SPC1, 200, 3, 23
SPCD, 600, 23, 3, 1.0
TLOAD2,
500, 600, , ACCE, 0.0, 0.004, 250., -90.
$
$ RBE MASS TO REMAINING BASE POINTS
$
RBE2, 101, 23, 3, 1, 12, 34, 45
$
$ SPECIFY INTEGRATION TIME STEPS
$
TSTEP, 100, 200, 2.0E-4, 1
$
ENDDATA
Слайд 24
Пример №7B
Модальный анализ переходного процесса с вынужденным перемещением
Слайд 25
Пример №7B. Модальный анализ переходного процесса с вынужденным
перемещением
Используя модальный метод, выполнить анализ переходного процесса колебаний модели.
Задано единичное синусоидальное ускорение заделки с частотой 250 Гц в Z направлении. Использовать конструкционное демпфирование g = 0,06, конвертировать его в вязкое на частоте 250 Гц. Включите в решение остаточный вектор.
Слайд 26
Входной файл для Примера №7B
ID SEMINAR, PROB7B
SOL 112
TIME
30
CEND
TITLE = TRANSIENT RESPONSE WITH BASE EXCITATION
SUBTITLE = USING
MODAL TRANSIENT METHOD, NO REDUCTION
ECHO = UNSORTED
SPC = 200
METHOD = 1000
SET 111 = 23, 33
DISPLACEMENT (SORT2) = 111
VELOCITY (SORT2) = 111
ACCELERATION (SORT2) = 111
SUBCASE 1
DLOAD = 500 DLOAD = 500
TSTEP = 100
$
OUTPUT (XYPLOT)
XGRID=YES
YGRID=YES
XTITLE= TIME (SEC)
YTITLE= BASE ACCELERATION
XYPLOT ACCELERATION RESPONSE / 23 (T3)
YTITLE= BASE DISPLACEMENT
XYPLOT DISP RESPONSE / 23 (T3)
YTITLE= TIP CENTER DISPLACEMENT RESPONSE
XYPLOT DISP RESPONSE / 33 (T3)
$
BEGIN BULK
$
$ PLATE MODEL DESCRIBED IN NORMAL MODES $EXAMPLE
$
INCLUDE ’plate.bdf’
PARAM, COUPMASS, 1
PARAM, WTMASS, 0.00259
$
$ SPECIFY STRUCTURAL DAMPING
$
PARAM, G, 0.06
PARAM, W3, 1571.
$
$ APPLY EDGE CONSTRAINTS
$
SPC1, 200, 12456, 1, 12, 23, 34, 45
Слайд 27
Входной файл для Примера №7B
PARAM, RESVEC, YES
EIGRL, 1000,
, , 10
$
$ APPLY ACCELERATION TO THE BASE
$
SPC1, 200,
3, 23
SPCD, 600, 23, 3, 1.0
TLOAD2, 500, 600, , ACCE, 0.0, 0.004, 250., -90.
$
$ RBE MASS TO REMAINING BASE POINTS
$
RBE2, 101, 23, 3, 1, 12, 34, 45
$
$ SPECIFY INTEGRATION TIME STEPS
$
TSTEP, 100, 200, 2.0E-4, 1
$
ENDDATA
Слайд 32
Пример №8A
Прямой анализ частотного отклика с вынужденным перемещением
Слайд 33
Пример №8A. Прямой анализ частотного отклика с вынужденным
перемещением
Используя прямой метод, определите частотный отклик плоской прямоугольной пластины
(модель создана в Примере №1) в диапазоне 20-1000 Гц с шагом 20 Гц. Задается вынужденное перемещение угла пластины амплитудой 0,1. Используйте конструкционное демпфирование g=0,06.
Слайд 34
Входной файл для Примера №8A
ID SEMINAR, PROB8A
SOL 108
TIME

30
CEND
TITLE= FREQUENCY RESPONSE DUE TO .1 DISPLACEMENT AT TIP
SUBTITLE=
DIRECT METHOD
ECHO= UNSORTED
SPC= 1
SET 111= 11, 33, 55
DISPLACEMENT(PHASE, SORT2)= 111
$SDISP(PHASE, SORT2)= ALL
set 222 = 11
OLOAD= 222
SUBCASE 1
DLOAD= 500
FREQUENCY= 100
$
OUTPUT (XYPLOT)
$
XTGRID= YES
YTGRID= YES
XBGRID= YES
YBGRID= YES
YTLOG= YES
YBLOG= NO
XTITLE= FREQUENCY (HZ)
YTTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER, MAGNITUDE
YBTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER, PHASE
XYPLOT DISP RESPONSE / 11 (T3RM, T3IP)
YTTITLE= DISPLACEMENT RESPONSE AT TIP CENTER, MAGNITUDE
YBTITLE= DISPLACEMENT RESPONSE AT TIP CENTER, PHASE
XYPLOT DISP RESPONSE / 33 (T3RM, T3IP)
YTTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER, MAGNITUDE
YBTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER, PHASE
XYPLOT DISP RESPONSE / 55 (T3RM, T3IP)
$
BEGIN BULK
$
$ PLATE MODEL DESCRIBED IN NORMAL MODES EXAMPLE
$
INCLUDE ’plate.bdf’
PARAM, COUPMASS, 1
PARAM, WTMASS, 0.00259
$
$ SPECIFY STRUCTURAL DAMPING
Слайд 35
Входной файл для Примера №8A
$
PARAM, G, 0.06
$
$
APPLY UNIT DISPLACEMENT AT TIP POINT
$
SPC1, 1, 3,
11
SPCD, 600, 11, 3, 0.1
$
RLOAD2, 500, 600, , ,310, , DISP
$
TABLED1, 310, 0., 1., 10000., 1., ENDT
$
$
$ SPECIFY FREQUENCY STEPS
$
FREQ1, 100, 20., 20., 49
$
ENDDATA
Слайд 40
Пример №8B
Модальный анализ частотного отклика с вынужденным перемещением
Слайд 41
Пример №8B. Модальный анализ частотного отклика с вынужденным
перемещением
Используя модальный метод, определите частотный отклик плоской прямоугольной пластины
(модель создана в Примере №1) в диапазоне 20-1000 Гц с шагом 20 Гц. Задается вынужденное перемещение угла пластины амплитудой 0,1. Используйте конструкционное демпфирование g=0,06. Включите в решение остаточный вектор.
Слайд 42
Входной файл для Примера №8B
ID SEMINAR, PROB8B
SOL 111
TIME

30
CEND
TITLE= FREQUENCY RESPONSE DUE TO .1 DISPLACEMENT AT TIP
SUBTITLE=
MODAL METHOD
ECHO= UNSORTED
SPC= 1
SET 111= 11, 33, 55
DISPLACEMENT(PHASE, SORT2)= 111
$SDISP(PHASE, SORT2)= ALL
set 222 = 11
OLOAD= 222
SUBCASE 1
METHOD= 1000
DLOAD= 500
FREQUENCY= 100
$
OUTPUT (XYPLOT)
$
XTGRID= YES
YTGRID= YES
XBGRID= YES
YBGRID= YES
YTLOG= YES
YBLOG= NO
XTITLE= FREQUENCY (HZ)
YTTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER, MAGNITUDE
YBTITLE= DISPLACEMENT RESPONSE AT LOADED CORNER, PHASE
XYPLOT DISP RESPONSE / 11 (T3RM, T3IP)
YTTITLE= DISPLACEMENT RESPONSE AT TIP CENTER, MAGNITUDE
YBTITLE= DISPLACEMENT RESPONSE AT TIP CENTER, PHASE
XYPLOT DISP RESPONSE / 33 (T3RM, T3IP)
YTTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER, MAGNITUDE
YBTITLE= DISPLACEMENT RESPONSE AT OPPOSITE CORNER, PHASE
XYPLOT DISP RESPONSE / 55 (T3RM, T3IP)
$
BEGIN BULK
$
$ PLATE MODEL DESCRIBED IN NORMAL MODES EXAMPLE
$
INCLUDE ’plate.bdf’
PARAM, COUPMASS, 1
PARAM, WTMASS, 0.00259
$
$ SPECIFY STRUCTURAL DAMPING
Слайд 43
Входной файл для Примера №8B
$
PARAM, G, 0.06
PARAM, RESVEC,
YES
EIGRL, 1000, , , 10
$
$ APPLY UNIT DISPLACEMENT
AT TIP POINT
$
SPC1, 1, 3, 11
SPCD, 600, 11, 3, 0.1
$
RLOAD2, 500, 600, , ,310, , DISP
$
TABLED1, 310, 0., 1., 10000., 1., ENDT
$
$
$ SPECIFY FREQUENCY STEPS
$
FREQ1, 100, 20., 20., 49
$
ENDDATA