Слайд 2
Раздел 15. Комплексный анализ собственных значений
КОМПЛЕКСНЫЙ АНАЛИЗ СОБСТВЕННЫХ
ЗНАЧЕНИЙ.… 15 - 3
РЕШЕНИЕ КОМПЛЕКСНОЙ СОБСТВЕННОЙ
ЗАДАЧИ – ТЕОРИЯ………………………..………………………
15 - 4
РЕШЕНИЕ КОМПЛЕКСНОЙ СОБСТВЕННОЙ
ЗАДАЧИ В MSC.Nastran…………………………………………. 15 - 5
УПРАВЛЕНИЕ РЕШЕНИЕМ ПРИ КОМПЛЕСНОМ
АНАЛИЗЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ……………..……….. 15 - 8
ПРИМЕР №12 – КОМПЛЕКСНЫЙ СОБСТВЕННЫЙ
АНАЛИЗ……………………………………………………………… 15 - 9
ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №12..………………………. 15 - 11
РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №12.…………………… 15 - 12
Слайд 3
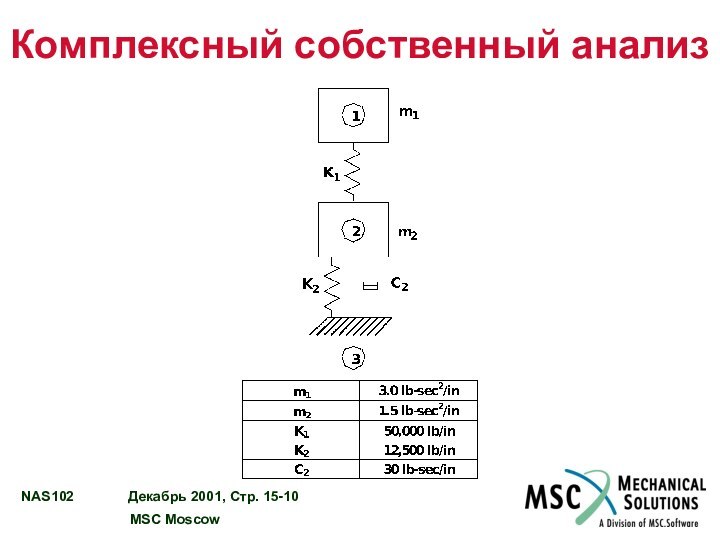
Комплексный анализ собственных значений
Используется для исследования устойчивости динамических
систем, включающих передаточные функции (включая сервомеханизмы и системы с
вращением)
Используется также для исследования собственных колебаний систем с демпфированием
Матрицы масс и жесткости могут быть несимметричными и содержать комплексные коэффициенты.
Дополнительная информация – в MSC.Nastran Advanced Dynamics User’s Guide.
Слайд 4
Решение комплексной собственной задачи - теория
Уравнение колебаний
где
p = α + iω
α – действительная часть
решения
ω – мнимая часть решения
При α < 0 динамическая система устойчива
Коэффициент демпфирования
Слайд 5
Решение комплексной собственной задачи в MSC.Nastran
Матрица B аналогична
используемой при анализе частотного отклика.
При использовании прямого метода уравнения
записываются с использованием матриц M, B и K размерности D-set (физические переменные плюс внешние переменные).
При модальном методе решения используются матрицы M, B и K размерности H-set (модальные переменные плюс внешние переменные), при этом предварительно вычисляются моды без учета демпфирования для преобразования переменных D-set в H-set.
Предусмотрено четыре метода решения: HESS, INV, DET и CLAN
Метод HESS (“верхний” метод Гессенберга) “родственен” методу GIV. Этот метод предполагает несингулярную матрицу M и может быть весьма затратен при решении больших задач. Следовательно, за исключением небольших задач рекомендуется использование модальной версии этого метода.
Метод HESS: решение уравнений в каноническом виде. Имеются два случая:
Системы с [B] = 0
Системы с [B] ≠ 0
Слайд 6
Решение комплексной собственной задачи в MSC.Nastran
При [B] =
0 решается
где
При [B] ≠ 0 решается
Комплексный метод INV
близок методу INV для действительной задачи. Пользователь должен указать область поиска корней на комплексной плоскости. Этот метод подходит для решения больших задач, причем допускается сингулярность матрицы масс M. Однако, этот метод более затратен в вычислительном плане по сравнению с методом HESS и менее надежен.
Метод DET не рекомендуется ввиду его неудобности и неэффективности.
Слайд 7
Решение комплексной собственной задачи в MSC.Nastran
Метод CLAN аналогичен
“действительному методу Ланцоша” – гибрид последовательного метода и метода
трансформации.
Метод поиска корней задается оператором EIGC в Bulk Data Section. В этом же операторе указывается область поиска корней. Оператор EIGC в Bulk Data Section инициируется оператором CMETHOD в Case Control Section.
Вычисление результатов методом модальных ускорений инициируется операторами PARAM,MODACC,0 и PARAM,DDRMM,-1
Использование метода модальных ускорений не влияет на результаты отыскания корней, он используется только на этапе получения решения в физических координатах.
Слайд 8
Управление решением при комплексном анализе собственных значений
Executive Control
Section
SOL
Case Control Section
CMETHOD (необходим при обоих методах)
METHOD (необходим при модальном
методе)
Bulk Data Section
EIGC (необходим при обоих методах)
EIGR или EIGRL (необходим при модальном методе)
Слайд 9
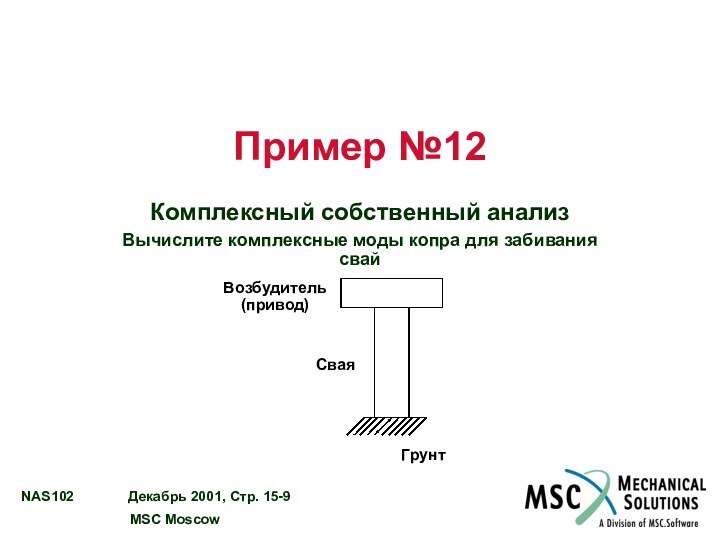
Пример №12
Комплексный собственный анализ
Вычислите комплексные моды копра для
забивания свай
Слайд 11
Входной файл для Примера №12
ID SEMINAR, PROB12
SOL 107
TIME
5
CEND
TITLE= TWO-DOF MODEL (IMAC 8, PG 891)
SUBTITLE= COMPLEX MODES
DISPLACEMENT=
ALL $ DEFAULT= REAL, IMAGINARY
SPC= 100
CMETHOD= 99
$
BEGIN BULK
$
$ COMPLEX EIGENVALUE EXTRACTION PARAMETERS
$
EIGC, 99, HESS, , , , , 4
$
$ DEFINE GRIDS, MASSES, AND STIFFNESSES
$ GRID 1 = EXCITER (X=2, MASS=3) 50K STIFFNESS BETWEEN GRIDS 1 AND 2
$ GRID 2 = PILE (X=1, MASS=3) 12.5K STIFFNESS BETWEEN GRIDS 2 AND 3
$ GRID 3 = BASE (X=0, FIX BASE)
$
GRID, 1, , 2., 0., 0.
GRID, 2, , 1., 0., 0.
GRID, 3, , 0., 0., 0.
GRDSET, , , , , , , 23456
CELAS2, 1, 50000., 1, 1, 2, 1
CELAS2, 2, 12500., 2, 1, 3, 1
CONM2, 201, 1, , 3.0
CONM2, 202, 2, , 1.5
SPC, 100, 3, 1
$
$ DEFINE DAMPER OF 30 BETWEEN GRIDS 2 AND 3
$
CVISC, 101, 1, 2, 3
PVISC, 1, 30.
$
ENDDATA
Слайд 12
Результаты решения Примера №12
1 TWO-DOF MODEL (IMAC

8, PG 891)
NOVEMBER 13, 2001 MSC.NASTRAN 4/ 9/01 PAGE 6
COMPLEX MODES
0
C O M P L E X E I G E N V A L U E S U M M A R Y
0 ROOT EXTRACTION EIGENVALUE FREQUENCY DAMPING
NO. ORDER (REAL) (IMAG) (CYCLES) COEFFICIENT
1 2 -2.660969E+00 -4.983521E+01 7.931520E+00 1.067907E-01
2 1 -2.660969E+00 4.983521E+01 7.931520E+00 1.067907E-01
3 4 -7.339031E+00 -2.360312E+02 3.756553E+01 6.218695E-02
4 3 -7.339031E+00 2.360312E+02 3.756553E+01 6.218695E-02
1 TWO-DOF MODEL (IMAC 8, PG 891) NOVEMBER 13, 2001 MSC.NASTRAN 4/ 9/01 PAGE 7
COMPLEX MODES
0
1 TWO-DOF MODEL (IMAC 8, PG 891) NOVEMBER 13, 2001 MSC.NASTRAN 4/ 9/01 PAGE 8
COMPLEX MODES
0
COMPLEX EIGENVALUE = -2.660969E+00, -4.983521E+01
C O M P L E X E I G E N V E C T O R NO. 1
(REAL/IMAGINARY)
POINT ID. TYPE T1 T2 T3 R1 R2 R3
0 1 G 1.000000E+00 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
0 2 G 8.514119E-01 0.0 0.0 0.0 0.0 0.0
1.591320E-02 0.0 0.0 0.0 0.0 0.0
0 3 G 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
1 TWO-DOF MODEL (IMAC 8, PG 891) NOVEMBER 13, 2001 MSC.NASTRAN 4/ 9/01 PAGE 9
COMPLEX MODES
0
COMPLEX EIGENVALUE = -2.660969E+00, 4.983521E+01
C O M P L E X E I G E N V E C T O R NO. 2
(REAL/IMAGINARY)
POINT ID. TYPE T1 T2 T3 R1 R2 R3
0 1 G 1.000000E+00 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
0 2 G 8.514119E-01 0.0 0.0 0.0 0.0 0.0
-1.591320E-02 0.0 0.0 0.0 0.0 0.0
0 3 G 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
Слайд 13
Результаты решения Примера №12
1 TWO-DOF MODEL (IMAC
8, PG 891)
NOVEMBER 13, 2001 MSC.NASTRAN 4/ 9/01 PAGE 10
COMPLEX MODES
0
COMPLEX EIGENVALUE = -7.339031E+00, -2.360312E+02
C O M P L E X E I G E N V E C T O R NO. 3
(REAL/IMAGINARY)
POINT ID. TYPE T1 T2 T3 R1 R2 R3
0 1 G -4.241094E-01 0.0 0.0 0.0 0.0 0.0
-3.768431E-02 0.0 0.0 0.0 0.0 0.0
0 2 G 1.000000E+00 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
0 3 G 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
1 TWO-DOF MODEL (IMAC 8, PG 891) NOVEMBER 13, 2001 MSC.NASTRAN 4/ 9/01 PAGE 11
COMPLEX MODES
0
COMPLEX EIGENVALUE = -7.339031E+00, 2.360312E+02
C O M P L E X E I G E N V E C T O R NO. 4
(REAL/IMAGINARY)
POINT ID. TYPE T1 T2 T3 R1 R2 R3
0 1 G -4.241094E-01 0.0 0.0 0.0 0.0 0.0
3.768431E-02 0.0 0.0 0.0 0.0 0.0
0 2 G 1.000000E+00 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0
0 3 G 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0





![MSC.Nastran 102 2001 - 15 Решение комплексной собственной задачи в MSC.NastranПри [B] = 0 решаетсягде При [B]](/img/tmb/11/1099195/b93a2c69f470c67d52f8a71d3b8da53d-720x.jpg)