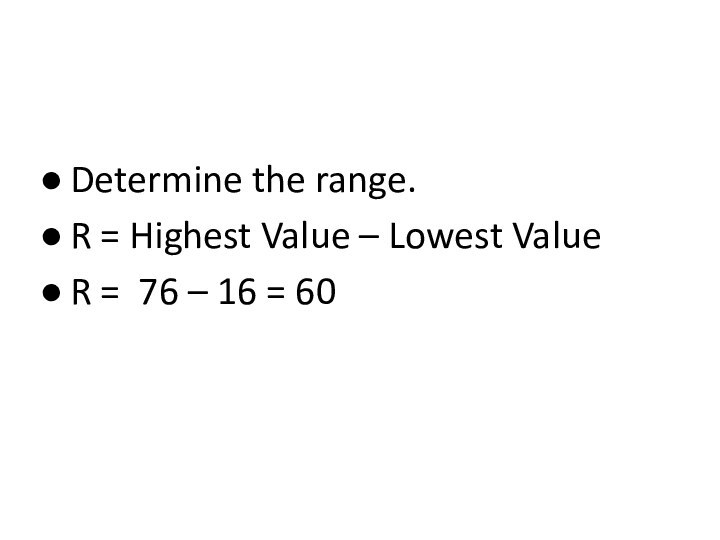Слайд 2
Learning Objectives
Overall: To give students a basic understanding
of best way of presentation of data
Specific: Students will
be able to
Understand Types of data
Draw Tables
Draw Graphs
Make Frequency distribution………….
Слайд 3
2.
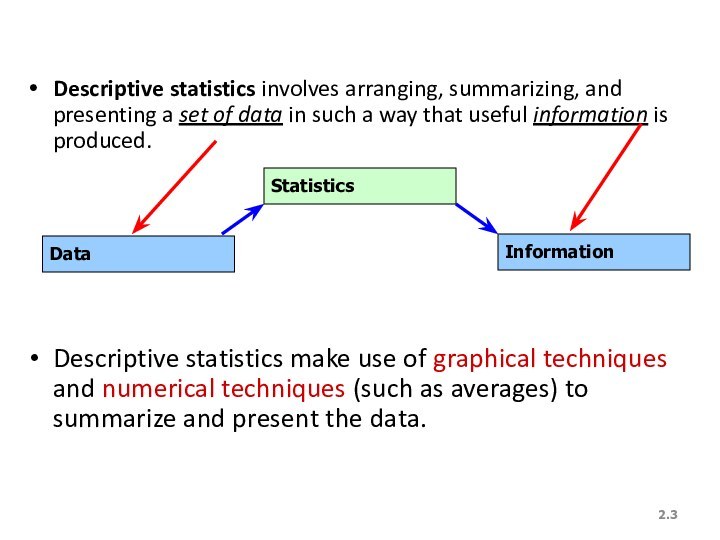
Descriptive statistics involves arranging, summarizing, and presenting a
set of data in such a way that useful
information is produced.
Descriptive statistics make use of graphical techniques and numerical techniques (such as averages) to summarize and present the data.
Data
Statistics
Information
Слайд 4
DATA MINING
Most companies routinely collect data – at
the cash register for each purchase, on the factory
floor from each step of production, or on the Internet from each visit to its website – resulting in huge databases containing potentially useful information about how to increase sales, how to improve production, or how to turn mouse clicks into purchases.
Слайд 5
DATA MINING is a collection of methods for
obtaining useful knowledge by analyzing large amounts of data,
often by searching for hidden patterns. Once a business has collected information for some purpose, it would be wasteful to leave it unexplored when it might be useful in many other ways. The goal of data mining is to obtain value from these vast stores of data, in order to improve the company with higher sales, lower costs, and better products. Here are just a few of the many areas of business in which data mining can be helpful:
Слайд 6
1. Marketing and sales: companies have lots of
information about past contacts with potential customers and their
results. These data can be mined for guidance on how (and when) to better reach customers in the future. One example is the difficult decision of when a store should reduce prices: reduce too soon and you lose money (on items that might have been sold for more); reduce too late and you may be stuck (with items no longer in season).
Слайд 7
Finance: Mining of financial data can be useful
in forming and evaluating investment strategies and in hedging
(or reducing) risk. In the stock markets alone, there are many companies: about 3,298 listed on the New York Stock Exchange and about 2,942 companies listed on the NASDAQ Stock Market. Historical information on price and volume (number of shares traded) is easily available to anyone interested in exploring investment strategies.
Слайд 8
Statistical methods, such as hypothesis testing, are helpful
as part of data mining distinguish random from systematic
behavior because stock that performed well last year will not necessarily perform well next year. Imagine that you toss 100 coins six times each and then carefully choose the one that came up “heads” all six times – this coin is not as special as it might seem!
Слайд 9
3. Product design: What particular combinations of
features are customers ordering in larger-than-expected quantities? The answers
could help you create products to appeal to a group of potential customers who would not take the trouble to place special orders.
Слайд 10
4. Production
Imagine a factory running 24/7 with
thousands of partially completed units, each with its bar
code, being carefully tracked by the computer system, with efficiency and quality being recorder as well. This is a tremendous source of information that can tell you about the kinds of situations that cause trouble (such as finding a machine that needs adjustment by noticing clusters of units that don’t work) or the kinds of situations that lead to extra-fast production of the highest quality.
Слайд 11
5. Fraud detections:
Fraud can affect many
areas of business, including consumer finance, insurance, and networks
(including telephone and the Internet). One of the best methods of protection involves mining data to distinguish between ordinary and fraudulent patterns of usage, then using the results to classify new transactions, and looking carefully at suspicious new occurrences to decide where or not fraud is actually involved.
Слайд 12
YOU once received a telephone call from your
credit card company asking you to verify recent transactions
– identified by its statistical analysis – that departed from your typical pattern of spending. One fraud risk identification system that helps detect fraudulent use of credit card is Falcon Fraud Manager from Fair Isaac, which uses the flexible “neural network” data-mining technique
Слайд 13
Data mining is a large task that involves
combining resources from many fields. Here is how statistics,
computer science, and optimization are used in data mining.
Слайд 14
Statistics: All of the basic activities of statistics
are involved: a design for collecting the data, exploring
for patterns, a modeling framework, estimation of features, and hypothesis testing to assess significance of patterns as a “reality check” on the results. Nearly every method in the rest of this lectures has the potential to be useful in data mining, depending on the database and the needs of the company.
Слайд 15
Some specialized statistical methods are particularly useful, including
classification analysis (also called discriminant analysis) to assign a
new case to a category (such as “likely purchaser” or “fraudulent”), cluster analysis to identify homogeneous group of individuals, and prediction analysis (also called regression analysis).
Слайд 16
Computer science: Efficient algorithms (computer instructions) are needed
for collecting, maintaining, organizing, and analyzing data. Creative methods
involving artificial intelligence are useful, including machine learning techniques for prediction analysis such as neural networks and boosting, to learn from the data by identifying useful patterns automatically. Some of these methods from computer science are closely related to statistical prediction analysis.
Слайд 17
Optimization:
These methods help you achieve a goal, which
might be very specific such as maximizing profits, lowering
production cost, finding new customers, developing profitable new product models, or increasing sales volume.
Слайд 18
Alternatively, the goal might be more vague such
as obtaining a better understanding of the different types
of customers you serve, characterizing the differences in production quality that occur under different circumstances, or identifying relationships that occur more or less consistently throughout the data. Optimization is often accomplished by adjusting the parameters of a model until the objective is achieved.
Слайд 19
WHAT IS PROBABILITY?
Probability is a what if tool
for understanding risk and uncertainty. Probability shows you the
likelihood, or chances, for each of the various potential future events, based on a set of assumptions about how the world works. For example, you might assume that you know basically how the world works (i.e., all of the details of process that will produce success or failure or payoffs in between). Probabilities of various outcomes would then be computed for each of several strategies to indicate how successful each strategy would be.
Слайд 20
You might learn, for example, that an international
project has only an 8% chance of success (i.e.
the probability of success is 0.08), but if you assume that the government can keep inflation low, then the chance of success rises to 35% - still very risky, but a much better situation than the 8% chance. Probability will not tell you whether to invest in the project, but it will help you keep your eyes open to the realities of the situation.
Слайд 21
Here are additional examples of situations where finding
the appropriate answer requires computing or estimating a probability
number:
Given the nature of an investment portfolio and a set of assumptions that describe how financial markets work, what are the chances that you will profit over a one-year horizon?
What are the chances of rain tomorrow? What are the chances that next winter will be cold enough so that your heating-oil business will make a profit?
Слайд 22
3. What are the chances that a foreign
country (where you have a manufacturing plant) will become
involved in civil war over the next two years?
4. What are the chances that the college student you just interviewed for a job will become a valued employee over the coming months?
Слайд 23
Probability is the inverse of statistics. Whereas statistics
helps you go from observed data to generalizations about
how the world works, probability goes the other direction: if you assume you know how the world works, then you can figure out what kinds of data you are likely to see and the likelihood for each.
Слайд 24
Probability also works together with statistics by providing
a solid foundation for statistical inference. When there is
uncertainty, you cannot know exactly what will happen, and there is some chance of error. Using probability, you will learn ways to control the error rate so that it is, say, less than 5% or less than 1% of the time.
Слайд 26
2.
Definitions…
A variable [Typically called a “random” variable since
we do not know it’s value until we observe
it] is some characteristic of a population or sample.
E.g. student grades, weight of a potato, # heads in 10 flips of a coin, etc.
Typically denoted with a capital letter: X, Y, Z…
The values of the variable are the range of possible values for a variable.
E.g. student marks (0..100)
Data are the observed values of a random variable.
E.g. student marks: {67, 74, 71, 83, 93, 55, 48}
Слайд 27
2.
We Deal with “2” Types of Data
Numerical/Quantitative Data
[Real Numbers]:
* height
* weight
* temperature
Qualitative/Categorical Data [Labels rather
than numbers]:
* favorite color
* Gender
* SES
Слайд 28
2.
Quantitative/Numerical Data…
Quantitative Data is further broken down into
Continuous
Data – Data can be any real number within
a given range. Normally measurement data [weights, Age, Prices, etc]
Discrete Data – Data can only be very specific values which we can list. Normally count data [# of firecrackers in a package of 100 that fail to pop, # of accidents on the UTA campus each week, etc]
Слайд 29
2.
Qualitative/Categorical Data
Nominal Data [has no natural order to
the values].
E.g. responses to questions about marital status:
Single = 1, Married = 2, Divorced = 3, Widowed = 4
Arithmetic operations don’t make any sense (e.g. does Widowed ÷ 2 = Married?!)
Ordinal Data [values have a natural order]:
E.g. College course rating system: poor = 1, fair = 2, good = 3, very good = 4, excellent = 5
Слайд 30
2.
Graphical & Tabular Techniques for Nominal Data…
The only
allowable calculation on nominal data is to count the
frequency of each value of the variable.
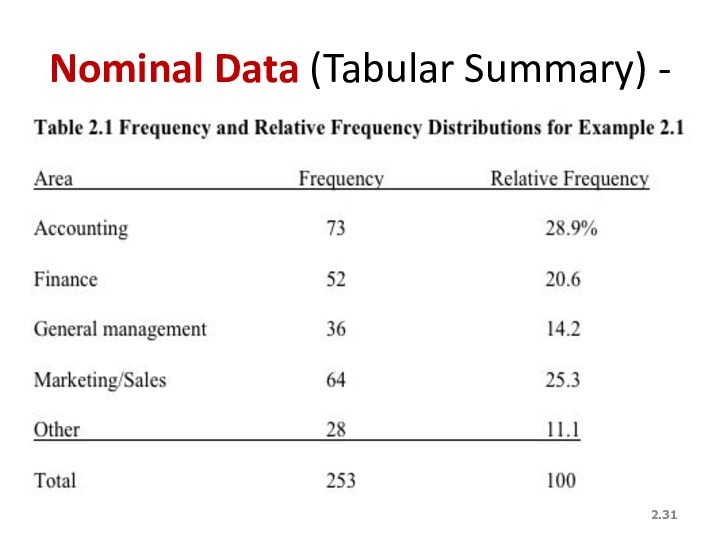
We can summarize the data in a table that presents the categories and their counts called a frequency distribution.
A relative frequency distribution lists the categories and the proportion with which each occurs.
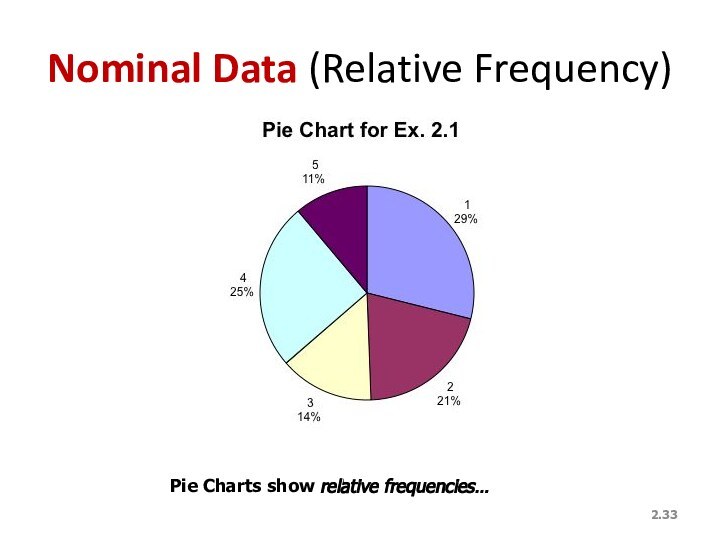
Since Nominal data has no order, if we arrange the outcomes from the most frequently occurring to the least frequently occurring, we call this a “pareto chart”
Слайд 31
2.
Nominal Data (Tabular Summary) -
Слайд 32
2.
Nominal Data (Frequency)
Bar Charts are often used to
display frequencies…
Is there a better way to order these?
Would Bar Chart
look different if we plotted “relative frequency” rather than “frequency”?
Слайд 33
2.
Nominal Data (Relative Frequency)
Pie Charts show relative frequencies…
Слайд 34
Frequency Distributions
Definition
A frequency distribution for qualitative data lists
all categories and the number of elements that belong
to each of the categories.
Слайд 35
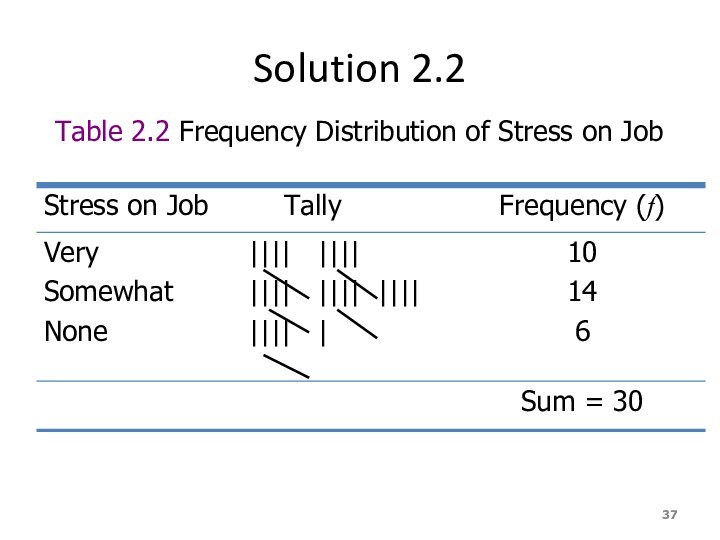
Example 2.2
A sample of 30 employees from large
companies was selected, and these employees were asked how
stressful their jobs were. The responses of these employees are recorded next where very represents very stressful, somewhat means somewhat stressful, and none stands for not stressful at all.
Слайд 36
Example 2.2
Construct a frequency distribution table for these
data.
Слайд 37
Solution 2.2
Table 2.2 Frequency Distribution of Stress on
Слайд 38
Relative Frequency and Percentage Distributions
Calculating Relative Frequency of
a Category
Слайд 39
Relative Frequency and Percentage Distributions cont.
Calculating Percentage
Percentage =
= (Relative frequency) · 100
Слайд 40
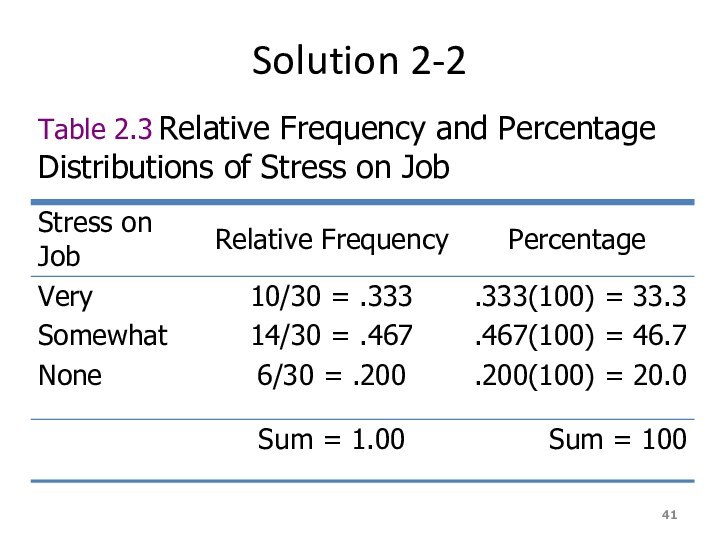
Example 2.3
Determine the relative frequency and percentage for
the data in Table 2.4.
Слайд 41
Solution 2-2
Table 2.3 Relative Frequency and Percentage Distributions
of Stress on Job
Слайд 42
Graphical Presentation of Qualitative Data
Definition
A graph made of
bars whose heights represent the frequencies of respective categories
is called a bar graph.
Слайд 43
Figure 2.2 Bar graph for the frequency distribution
of Table 2.3
Слайд 44
Graphical Presentation of Qualitative Data cont.
Definition
A circle divided
into portions that represent the relative frequencies or percentages
of a population or a sample belonging to different categories is called a pie chart.
Слайд 45
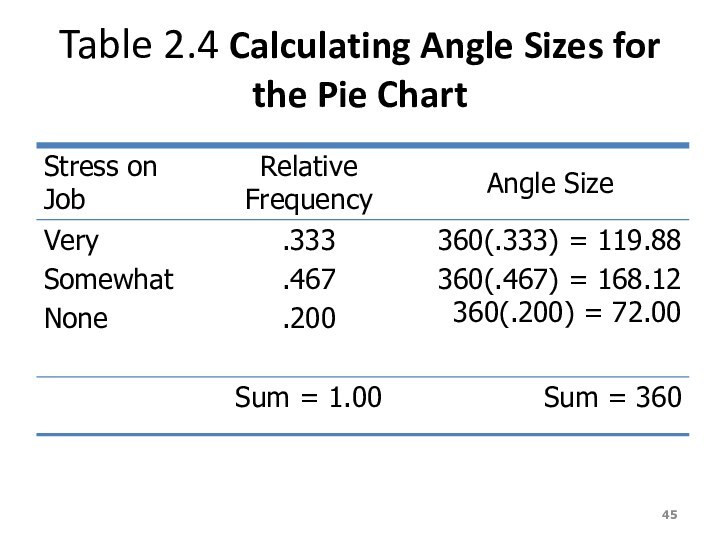
Table 2.4 Calculating Angle Sizes for the Pie
Chart
Слайд 46
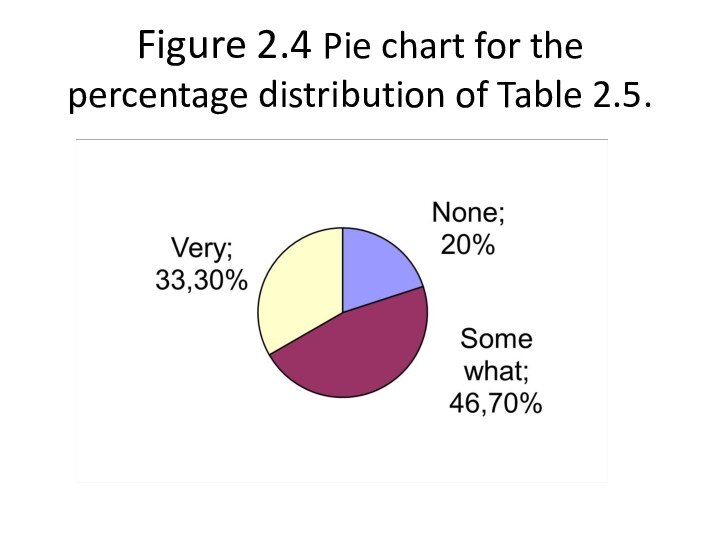
Figure 2.4 Pie chart for the percentage distribution
of Table 2.5.
Слайд 47
ORGANIZING AND GRAPHING QUANTITATIVE DATA
Frequency Distributions
Constructing Frequency Distribution
Tables
Relative and Percentage Distributions
Graphing Grouped Data
Histograms
Polygons
Слайд 48
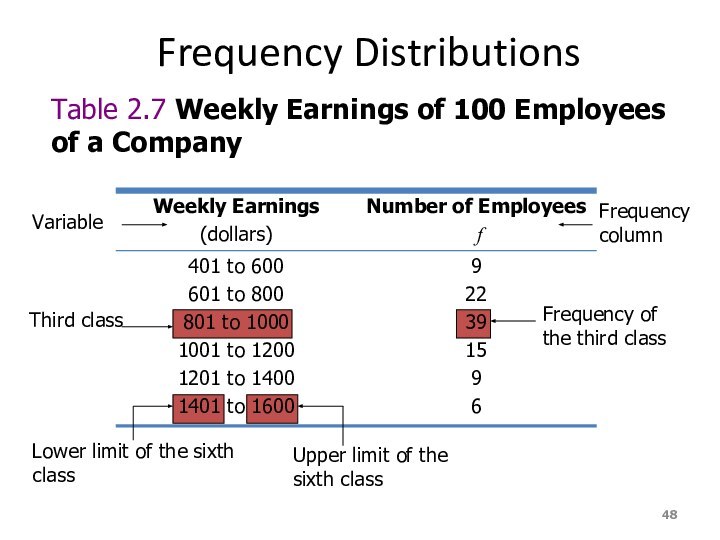
Frequency Distributions
Table 2.7 Weekly Earnings of 100 Employees
of a Company
Variable
Third class
Lower limit of the sixth
class
Upper limit of the sixth class
Frequency of the third class
Frequency column
Слайд 49
Frequency Distributions cont.
Definition
A frequency distribution for quantitative
data lists all the classes and the number of
values that belong to each class. Data presented in the form of a frequency distribution are called grouped data.
Слайд 50
Essential Question :
How do we construct a frequency
distribution table?
Слайд 51
Process of Constructing a Frequency Table
STEP 1:
Determine the range.
R = Highest Value – Lowest
Value
Слайд 52
STEP 2. Determine the tentative number of classes
(k)
k = 1 + 3.322 log N
Always round
– off
Note: The number of classes should be between 5 and 20. The actual number of classes may be affected by convenience or other subjective factors
Слайд 53
STEP 3. Find the class width by dividing
the range by the number of classes.
(Always round –
off )
Слайд 54
STEP 4. Write the classes or categories starting
with the lowest score. Stop when the class already
includes the highest score.
Add the class width to the starting point to get the second lower class limit. Add the class width to the second lower class limit to get the third, and so on. List the lower class limits in a vertical column and enter the upper class limits, which can be easily identified at this stage.
Слайд 55
STEP 5. Determine the frequency for each class
by referring to the tally columns and present the
results in a table.
Слайд 56
When constructing frequency tables, the following guidelines should
be followed.
The classes must be mutually exclusive. That is,
each score must belong to exactly one class.
Include all classes, even if the frequency might be zero.
Слайд 57
3. All classes should have the same width,
although it is sometimes impossible to avoid open –
ended intervals such as “65 years or older”.
4. The number of classes should be between 5 and 20.
Слайд 58
Let’s Try!!!
Time magazine collected information on all
464 people who died from gunfire in the Philippines
during one week. Here are the ages of 50 men randomly selected from that population. Construct a frequency distribution table.
Слайд 59
19 18 30 40 41 33 73
25
23 25 21 33 65 17 20 76
47 69
20 31 18 24 35 24
17 36 65 70 22 25 65 16
24 29 42 37 26 46 27 63
21 27 23 25 71 37 75 25
27 23
Слайд 60
Determine the range.
R = Highest Value – Lowest
Value
R = 76 – 16 = 60
Слайд 61
Determine the tentative number of classes (K).
K = 1 + 3. 322 log N
= 1 + 3.322 log 50
= 1 + 3.322 (1.69897) = 6.64
*Round – off the result to the next integer if the decimal part exceeds 0.
K = 7
Слайд 62
Find the class width (c).
* Round – off
the quotient if the decimal part exceeds 0.
Слайд 63
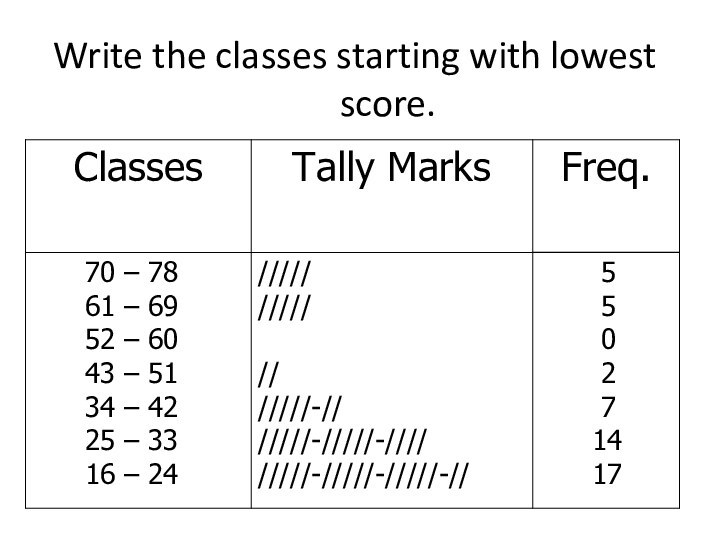
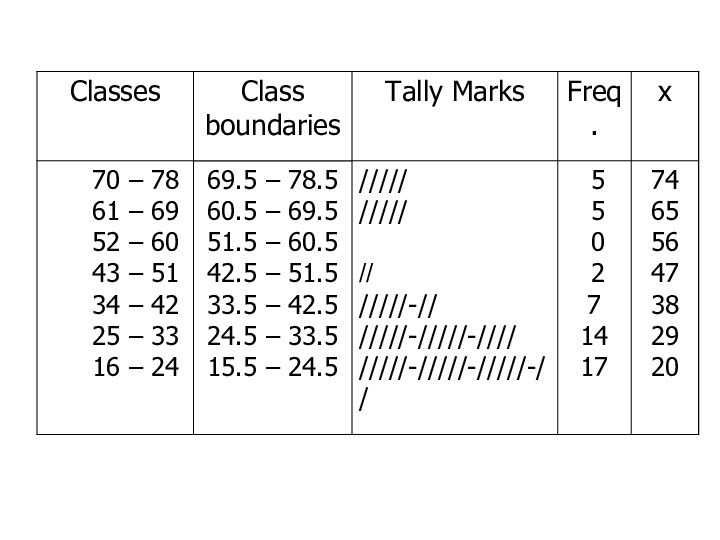
Write the classes starting with lowest score.
Слайд 64
Using Table:
What is the lower class limit of
the highest class?
Upper class limit of the lowest
class?
Find the class mark of the class 43 – 51.
What is the frequency of the class 16 – 24?
Слайд 66
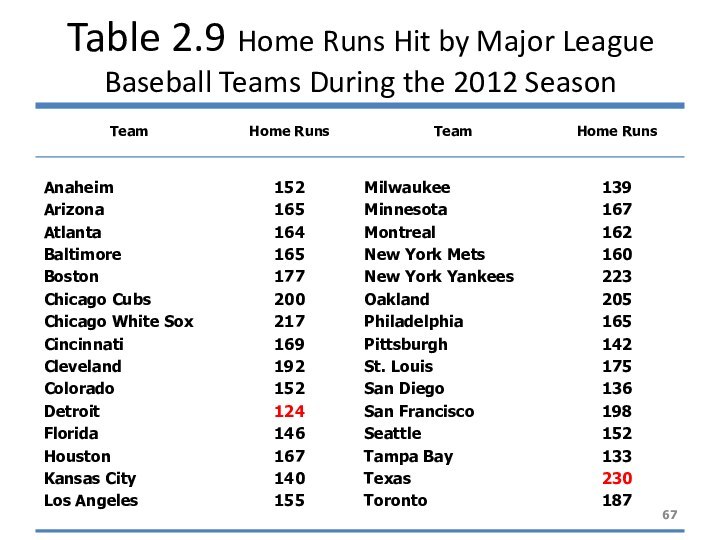
Example
Table 2.9 gives the total home runs
hit by all players of each of the 30
Major League Baseball teams during the 2012 season. Construct a frequency distribution table.
Слайд 67
Table 2.9 Home Runs Hit by Major League
Baseball Teams During the 2012 Season
Слайд 68
Solution 2-3
Now we round this approximate width to
a convenient number – say, 22.
Слайд 69
Solution 2-3
The lower limit of the first class
can be taken as 124 or any number less
than 124. Suppose we take 124 as the lower limit of the first class. Then our classes will be
124 – 145, 146 – 167, 168 – 189, 190 – 211, and 212 - 233
Слайд 70
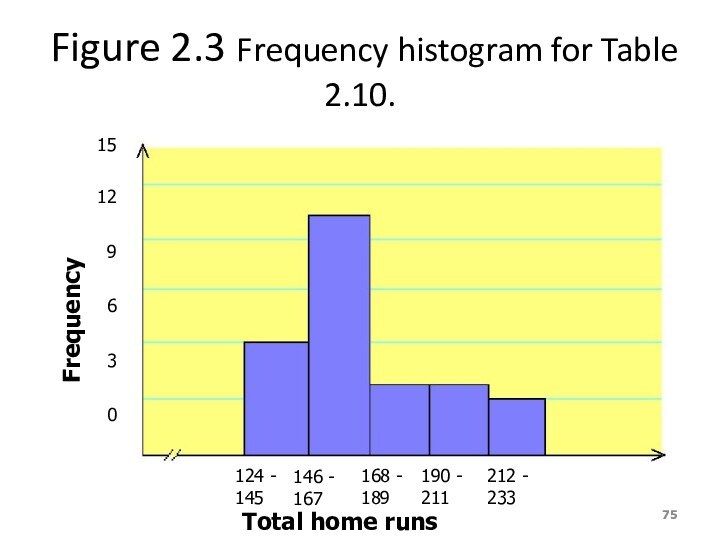
Table 2.10 Frequency Distribution for the Data of
Table 2.9
Слайд 71
Relative Frequency and Percentage Distributions
Relative Frequency and Percentage
Distributions
Слайд 72
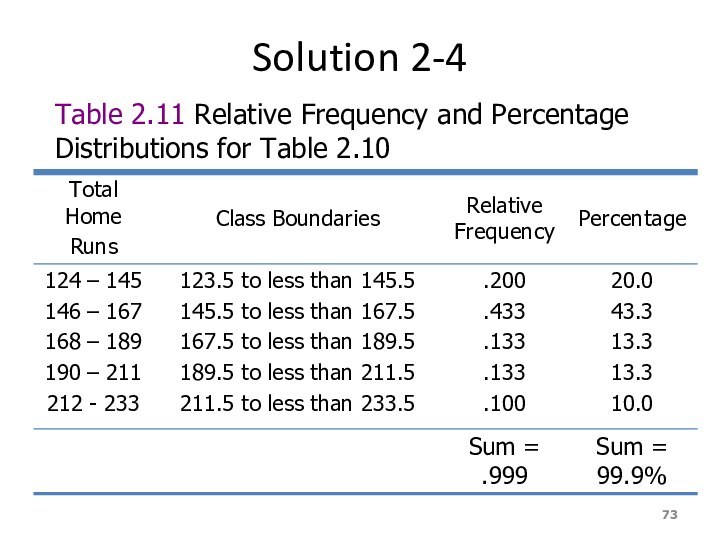
Example 2-4
Calculate the relative frequencies and percentages for
Table 2.10
Слайд 73
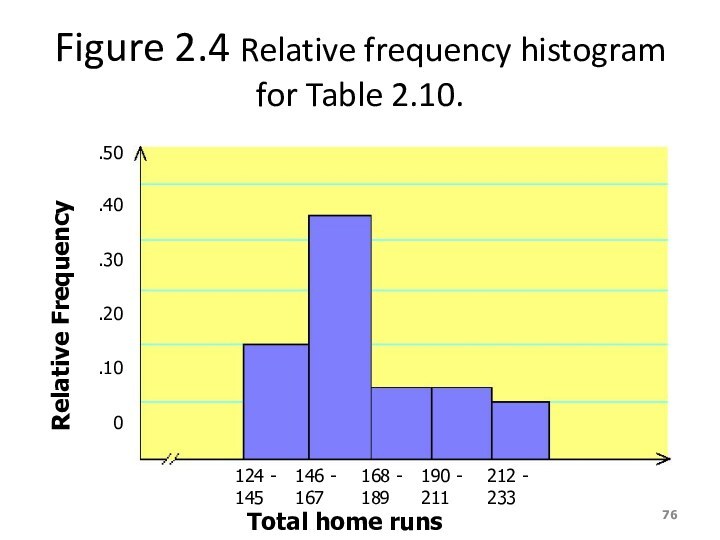
Solution 2-4
Table 2.11 Relative Frequency and Percentage Distributions
for Table 2.10
Слайд 74
Graphing Grouped Data
Definition
A histogram is a graph in
which classes are marked on the horizontal axis and
the frequencies, relative frequencies, or percentages are marked on the vertical axis. The frequencies, relative frequencies, or percentages are represented by the heights of the bars. In a histogram, the bars are drawn adjacent to each other.
Слайд 75
Figure 2.3 Frequency histogram for Table 2.10.
124 -
145
146 - 167
168 - 189
190 - 211
212 - 233
Total
home runs
15
12
9
6
3
0
Frequency
Слайд 76
Figure 2.4 Relative frequency histogram for Table 2.10.
124
- 145
146 - 167
168 - 189
190 - 211
212 -
233
Total home runs
.50
.40
.30
.20
.10
0
Relative Frequency
Слайд 77
Graphing Grouped Data cont.
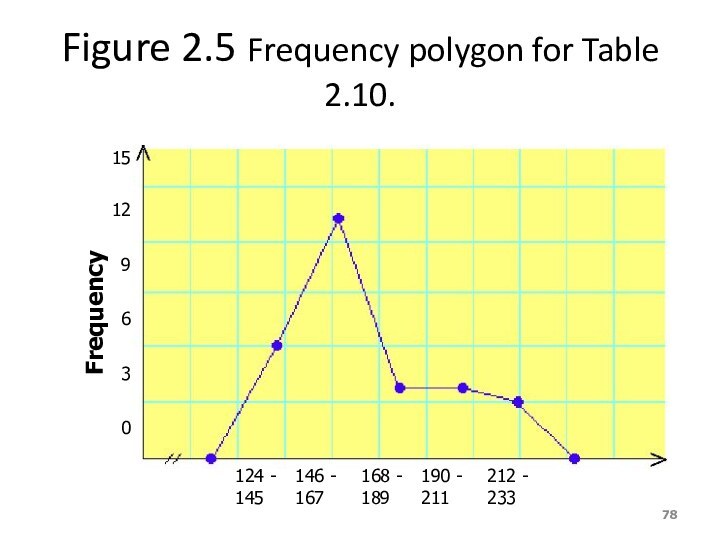
Definition
A graph formed by joining
the midpoints of the tops of successive bars in
a histogram with straight lines is called a polygon.
Слайд 78
Figure 2.5 Frequency polygon for Table 2.10.
124 -
145
146 - 167
168 - 189
190 - 211
212 - 233
15
12
9
6
3
0
Frequency
Слайд 79
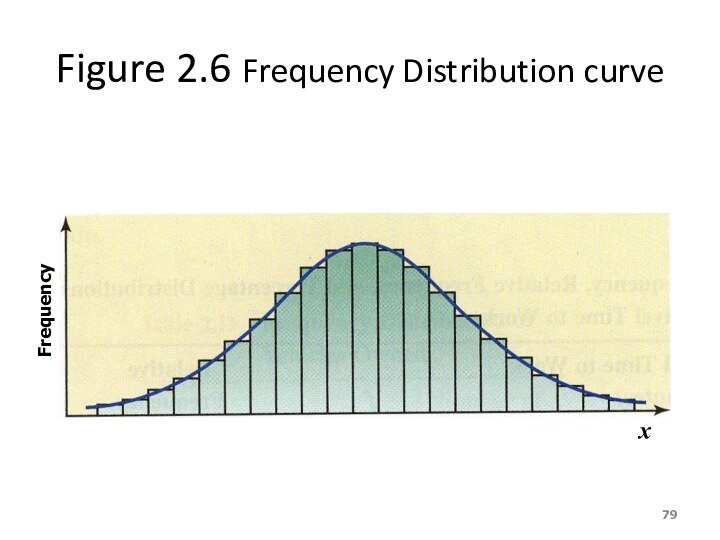
Figure 2.6 Frequency Distribution curve
Frequency
x
Слайд 80
Example 2-5
The following data give the average travel
time from home to work (in minutes) for 50
states. The data are based on a sample survey of 700,000 households conducted by the Census Bureau (USA TODAY, August 6, 2013).
Слайд 81
Example 2-5
Construct a frequency distribution table.
Calculate the relative frequencies and percentages for all classes.
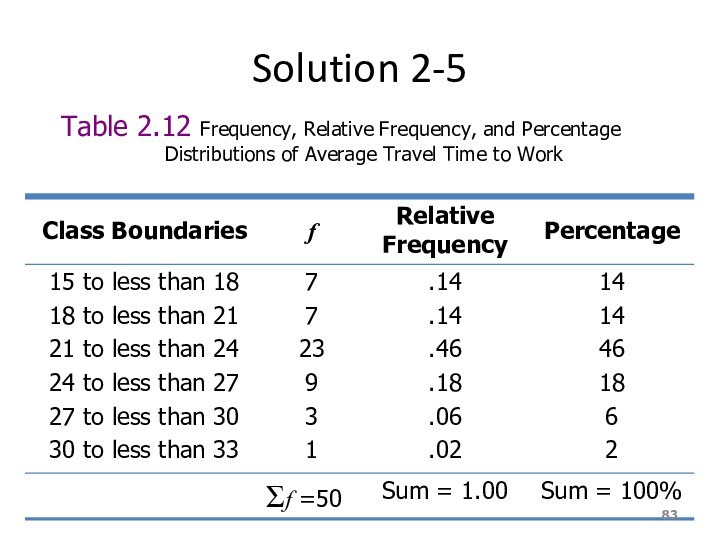
Слайд 83
Solution 2-5
Table 2.12 Frequency, Relative Frequency, and Percentage
Distributions of Average
Travel Time to Work
Слайд 84
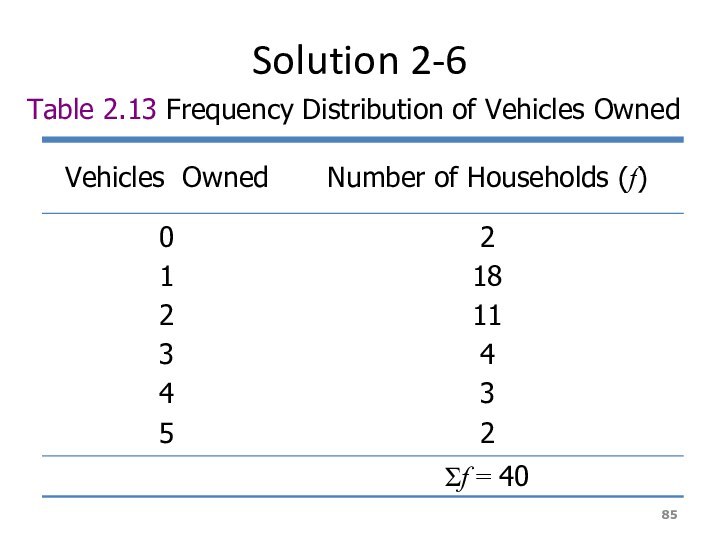
Example 2-6
The administration in a
large city wanted to know the distribution of vehicles
owned by households in that city. A sample of 40 randomly selected households from this city produced the following data on the number of vehicles owned:
5 1 1 2 0 1 1 2 1 1
1 3 3 0 2 5 1 2 3 4
2 1 2 2 1 2 2 1 1 1
4 2 1 1 2 1 1 4 1 3
Construct a frequency distribution table for these data, and draw a bar graph.
Слайд 85
Solution 2-6
Table 2.13 Frequency Distribution of Vehicles Owned
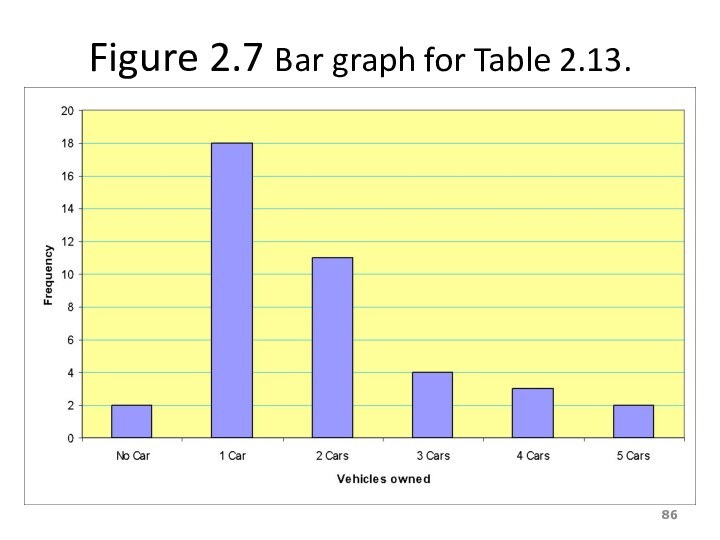
Слайд 86
Figure 2.7 Bar graph for Table 2.13.
Слайд 87
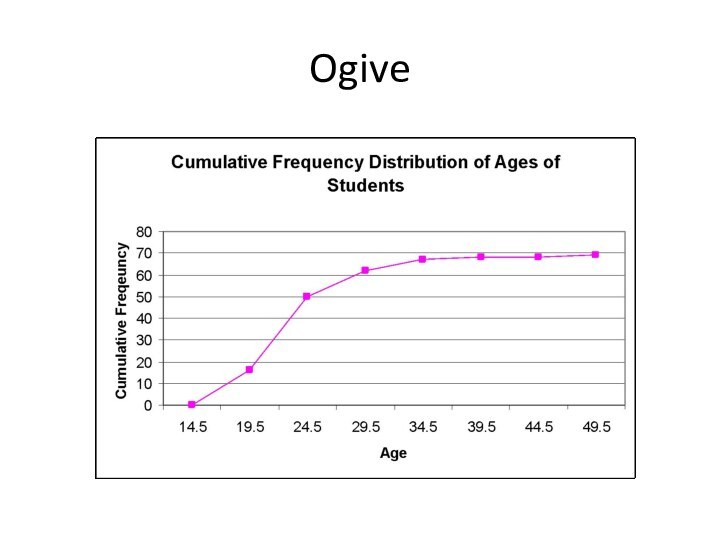
Ogive
The ogive is a graph that represents the
cumulative frequencies for the classes in a frequency distribution
Step
1. Find the cumulative frequency for each class.
Step 2. Draw the x and y axes. Label the x-axis with the class boundaries.
Step 3. Plot the cumulative frequency at each upper class boundary.

























![Organizing data graphical and nabular descriptive techniques 2.We Deal with “2” Types of DataNumerical/Quantitative Data [Real Numbers]: * height * weight *](/img/tmb/15/1449464/1b12d07a44ce2d13893bec7f81499341-720x.jpg)

![Organizing data graphical and nabular descriptive techniques 2.Qualitative/Categorical DataNominal Data [has no natural order to the values]. E.g. responses](/img/tmb/15/1449464/abdb242e196c9fae90eac4c66308345c-720x.jpg)