Слайд 2
Алгебра логики — это раздел математики, изучающий высказывания,
рассматриваемые со стороны их логических значений (истинности или ложности)
и логических операций над ними.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Слайд 3
Понятие высказывания
Высказывание - это
повествовательное предложение, относительно которого можно определенно сказать, истинно оно
или ложно.
Например: "Луна - спутник Земли" - истинное высказывание, "Два больше трех" - ложное высказывание. "Как вы себя чувствуете?", "Будь внимателен!" — не являются высказываниями и в алгебре высказываний не рассматриваются.
Высказывания принято обозначать буквами латинского алфавита. Так, высказывание "Трава — зеленая" можно обозначить буквой А, "Лев -птица" - буквой В и т. д.
Слайд 4
Значения истинности высказываний
В алгебре высказываний отвлекаются от конкретного
содержания высказывания и интересуются лишь вопросом, является ли оно
истинным или ложным..
Каждому верному высказыванию присваивается значение истинности 1 (истинно), каждому неверному - значение истинности 0 (ложно).
Например, А = 1, В = 0.
Слайд 5
Операции над высказываниями
Над высказываниями можно производить логические операции.
В результате выполнения операций получаются новые высказывания, истинность которых
определяется истинностью исходных высказываний и характером логических операций.
Слайд 6
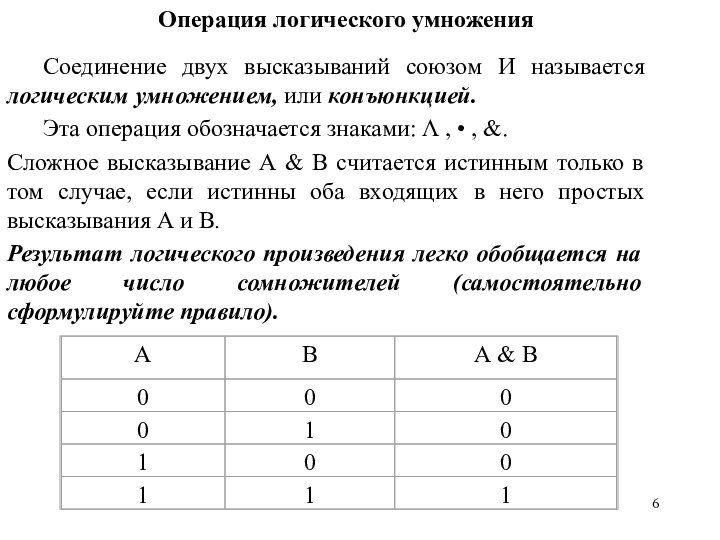
Операция логического умножения
Соединение двух высказываний союзом И называется
логическим умножением, или конъюнкцией.
Эта операция обозначается знаками: Λ ,
• , &.
Сложное высказывание А & В считается истинным только в том случае, если истинны оба входящих в него простых высказывания А и В.
Результат логического произведения легко обобщается на любое число сомножителей (самостоятельно сформулируйте правило).
Слайд 7
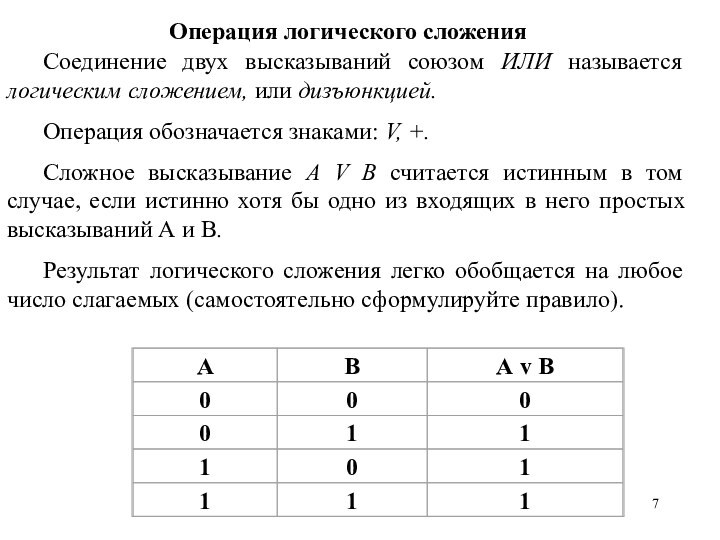
Операция логического сложения
Соединение двух высказываний союзом ИЛИ называется
логическим сложением, или дизъюнкцией.
Операция обозначается знаками: V, +.
Сложное высказывание A V В считается истинным в том случае, если истинно хотя бы одно из входящих в него простых высказываний А и В.
Результат логического сложения легко обобщается на любое число слагаемых (самостоятельно сформулируйте правило).
Слайд 8
Операция отрицания
Присоединение частицы НЕ к высказыванию А называется
отрицанием, или инверсией.
Операция обозначается ~А или ⎤ А
, (читается: не А).
Если высказывание истинно, то его отрицание ложно, и наоборот.
Слайд 9
Операция импликации (если-то)
ЕСЛИ-ТО Операция, выражаемая связками
"если ..., то", "из ... следует", "... влечет ...",
называется импликацией (лат. implico — тесно связаны) и обозначается знаком . Высказывание ложно тогда и только тогда, когда А истинно, а В ложно.
Слайд 10
Операция импликации
Импликация выражается словосочетанием « если…, то…». По
определению импликация А → В истинна всегда за исключением
случая, когда А истинно, а В ложно.
Слайд 11
Операция эквивалентности (равносильно)
РАВНОСИЛЬНО Операция, выражаемая связками "тогда
и только тогда", "необходимо и достаточно", "... равносильно ...",
называется эквиваленцией или двойной импликацией и обозначается знаком или ~. Высказывание истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
Слайд 12
Операция эквивалентности
Операция «Эквивалентность» обозначается знаками ↔,=.
Сложное высказывание
А ↔ В( читается А эквивалентно В) истинно тогда
и только тогда, когда А – истинно и В истинно или А – ложно и В – ложно. В остальных случаях А ↔ В ложно.
Слайд 13
A | B = ⎤ (A&B)
Операция штрих
Шеффера
Слайд 15
Операция «Сложение по модулю два»
A ⊕ B =
A& ⎤ B ∨ ⎤ A& B
Слайд 16
ЛОГИЧЕСКИЕ ФОРМУЛЫ
Логическая формула –
это логические переменные,
связанные логическими операциями.
Слайд 18
Порядок выполнения логических операций
Отрицание - операция первой ступени.
Конъюнкция
(логическое умножение) − операция второй ступени.
Дизъюнкции (логического сложения) −
операция третьей ступени.
Скобки используются для изменения порядка выполнения операций.
Слайд 19
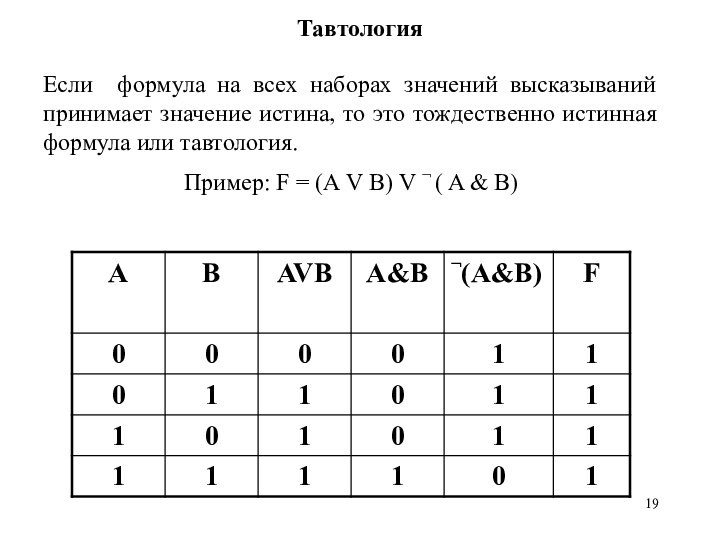
Тавтология
Если формула на всех наборах значений высказываний принимает
значение истина, то это тождественно истинная формула или тавтология.
Пример:
F = (А V B) V ¬ ( A & B)
Слайд 20
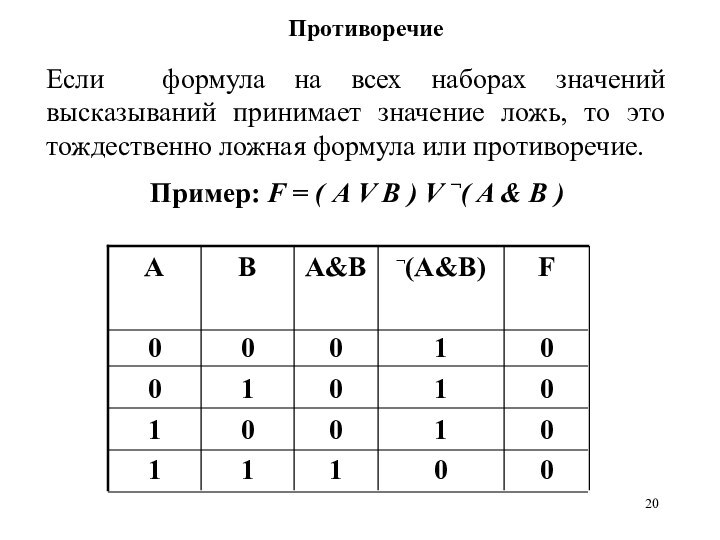
Противоречие
Если формула на всех наборах значений высказываний принимает
значение ложь, то это тождественно ложная формула или противоречие.
Пример:
F = ( А V B ) V ¬( A & B )
Слайд 21
В качестве другого примера рассмотрим формулу А .
, которой соответствует, например, высказывание "Катя самая высокая
девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Слайд 22
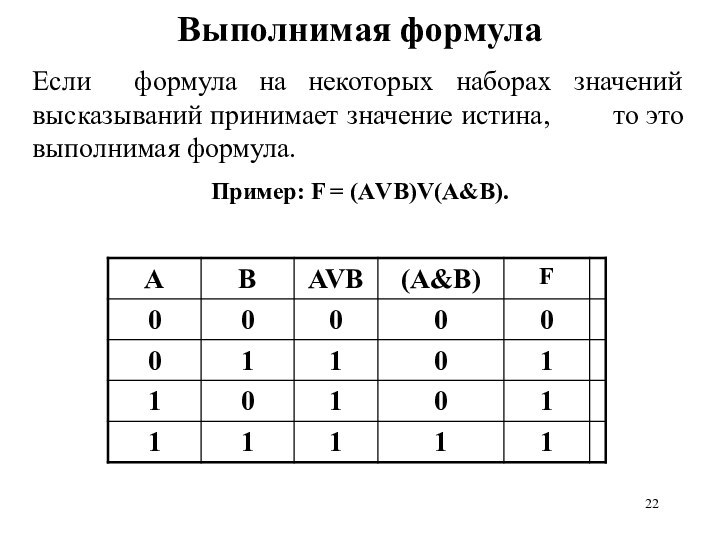
Выполнимая формула
Если формула на некоторых наборах значений
высказываний принимает значение истина, то это
выполнимая формула.
Пример: F = (АVB)V(A&B).
Слайд 23
Если две формулы А и В одновременно, то
есть при одинаковых наборах значений входящих в них переменных,
принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом " " Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Слайд 25
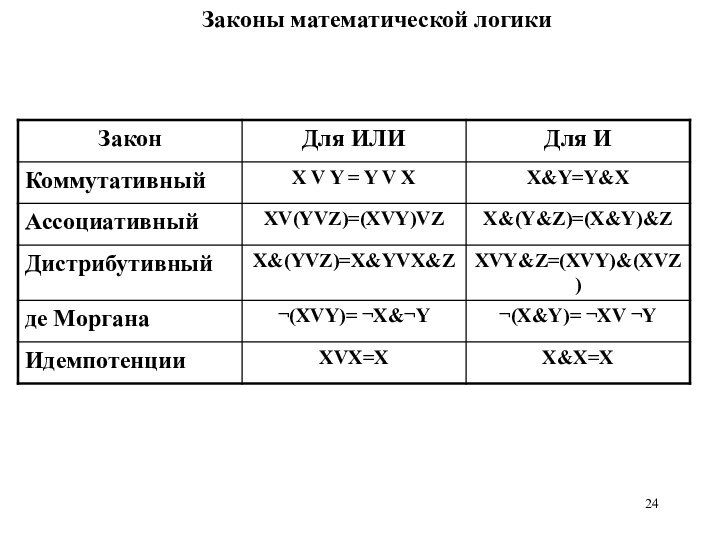
Законы математической логики. Продолжение.
Слайд 26
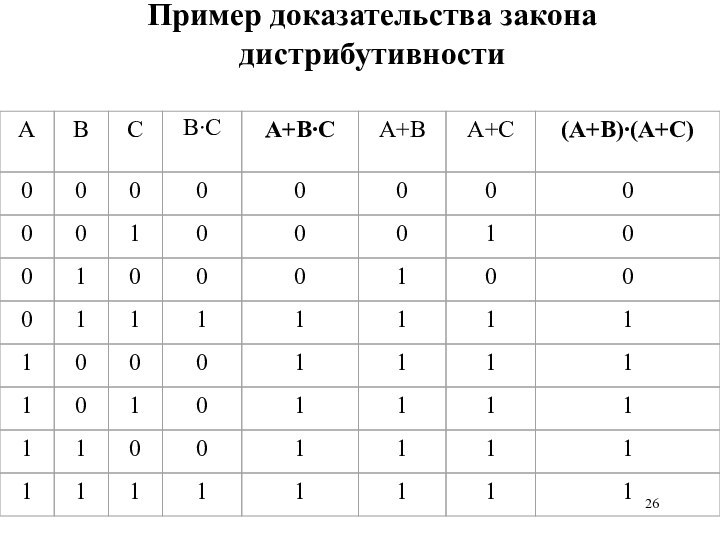
Пример доказательства закона дистрибутивности
Слайд 27
Преобразования логических выражений
Формулы для отрицания:
Формулы для дизъюнкции:
Формулы
для конъюнкции:
Правило действия со скобками:
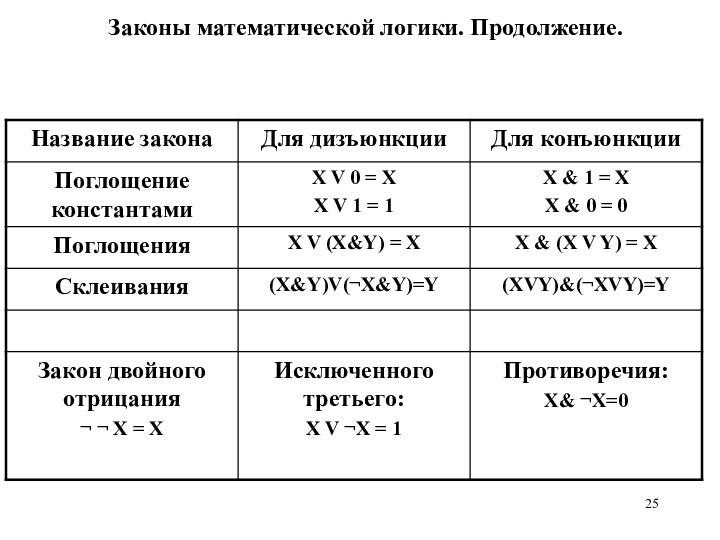
Операция поглощения:
Операция склеивания:
Формулы де Моргана:
Слайд 29
КАК УПРОСТИТЬ ЛОГИЧЕСКУЮ ФОРМУЛУ?
Равносильные преобразования логических формул
имеют то же назначение, что и преобразования формул в
обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
Слайд 30
Под упрощением формулы, не содержащей операций импликации и
эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо
содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Слайд 31
ПРИЕМЫ И СПОСОБЫ, ПРИМЕНЯЕМЫЕ ПРИ УПРОЩЕНИИ ЛОГИЧЕСКИХ ФОРМУЛ
Законы алгебры логики применяются в следующей последовательности: правило де
Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами.
Слайд 32
Примеры упрощения формул
Пример 1.
(применяется правило де Моргана, выносится
за скобки общий множитель, используется правило операций переменной с
её инверсией).
Пример 2.
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания).
Слайд 33
Пример 3.
(повторяется второй сомножитель, что разрешено законом
идемпотенции; затем комбинируются два первых и два последних сомножителя
и используется закон склеивания);
Слайд 34
Пример 4.
(вводится вспомогательный логический сомножитель (
); затем комбинируются два крайних и два средних логических
слагаемых и используется закон поглощения);
Слайд 35
Пример 5.
(сначала добиваемся, чтобы знак отрицания стоял только
перед отдельными переменными, а не перед их комбинациями, для
этого дважды применяем правило де Моргана; затем используем закон двойного отрицания).
Слайд 36
Пример 5
(сначала добиваемся, чтобы знак отрицания стоял только
перед отдельными переменными, а не перед их комбинациями, для
этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
Слайд 37
Пример 6
(выносятся за скобки общие множители; применяется правило
операций с константами).
Слайд 38
Пример 7
(к отрицаниям неэлементарных формул применяется правило де
Моргана; используются законы двойного отрицания и склеивания).
Слайд 39
Пример 8
(общий множитель x выносится за скобки, комбинируются
слагаемые в скобках — первое с третьим и второе
с четвертым, к дизъюнкции применяется правило операции переменной с её инверсией);
Слайд 40
Пример 9
(используются распределительный закон для дизъюнкции, правило операции
переменной с ее инверсией, правило операций с константами, переместительный
закон и распределительный закон для конъюнкции).
Слайд 41
Пример 10
(используются правило де Моргана, закон двойного отрицания
и закон поглощения).
Из этих примеров видно, что при
упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
Слайд 42
Какая связь между алгеброй логики и двоичным кодированием?
Математический
аппарат алгебры логики очень удобен для описания того, как
функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Слайд 43
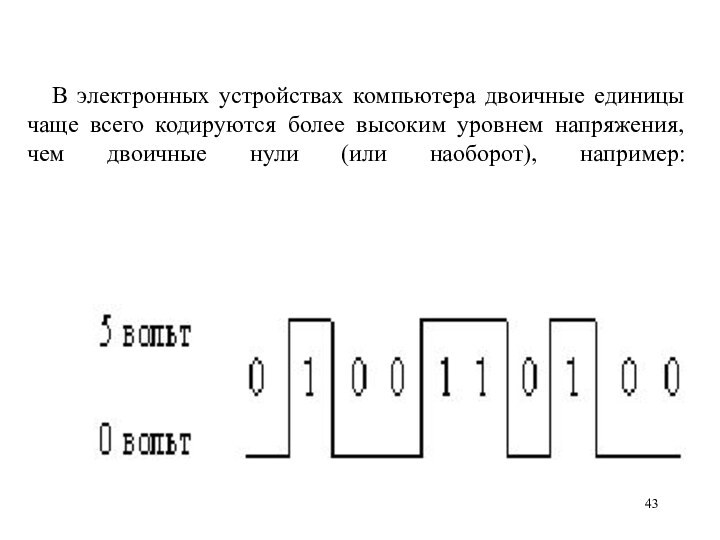
В электронных устройствах компьютера двоичные единицы чаще всего
кодируются более высоким уровнем напряжения, чем двоичные нули (или
наоборот), например:
Слайд 44
Переключательная схема
В компьютерах и других автоматических устройствах широко
применяются электрические схемы, содержащие сотни и тысячи переключательных элементов:
реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики.
Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.
Слайд 45
1.
Схема не содержит переключателей и проводит ток всегда,
следовательно F=1.
2.
Схема содержит один постоянно разомкнутый контакт, следовательно F=0.
3.
Схема
проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x.
4.
Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) = ;
Слайд 46
5.
Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y.
6.
Схема проводит ток, когда
хотя бы один из переключателей замкнут, следовательно, F(x)=x v y.
7.
Схема состоит из двух параллельных ветвей и описывается функцией
Слайд 47
Две схемы называются равносильными, если через одну из
них проходит ток тогда и только тогда, когда он
проходит через другую (при одном и том же входном сигнале).
При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.
СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём этапам:
составлению функции проводимости по таблице истинности, отражающей эти условия;
упрощению этой функции;
построению соответствующей схемы.
Слайд 48
Пример 1
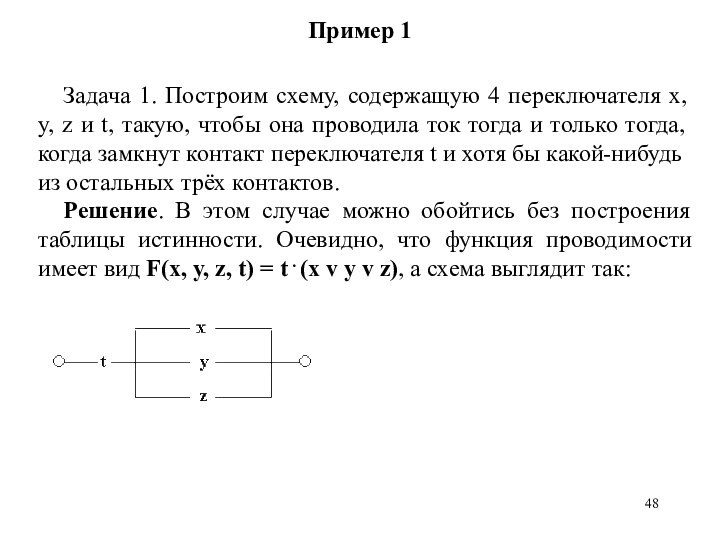
Задача 1. Построим схему, содержащую 4 переключателя
x, y, z и t, такую, чтобы она проводила
ток тогда и только тогда, когда замкнут контакт переключателя t и хотя бы какой-нибудь из остальных трёх контактов.
Решение. В этом случае можно обойтись без построения таблицы истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) = t . (x v y v z), а схема выглядит так:
Слайд 49
Пример 2
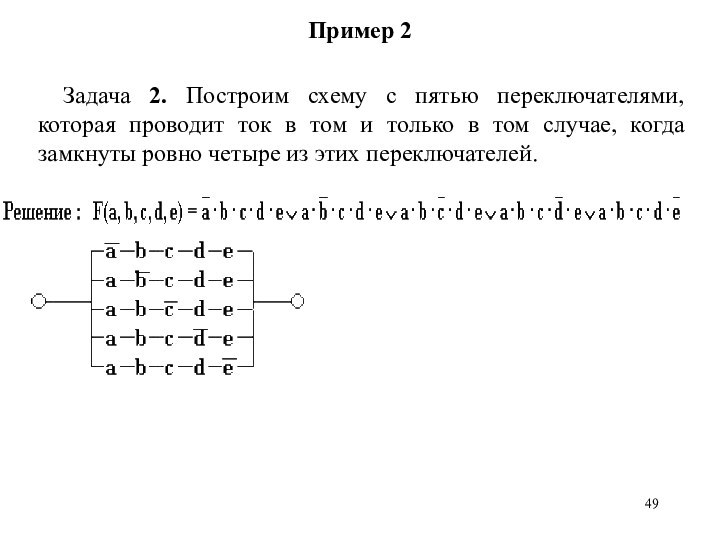
Задача 2. Построим схему с пятью переключателями,
которая проводит ток в том и только в том
случае, когда замкнуты ровно четыре из этих переключателей.
Слайд 50
Пример 3
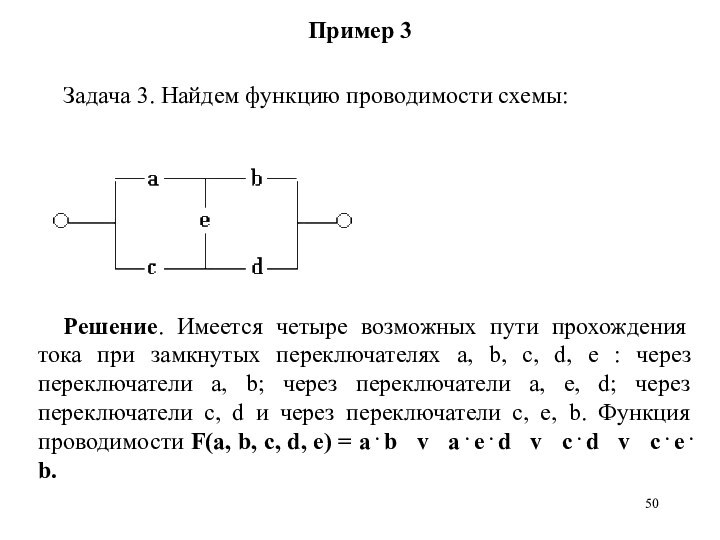
Задача 3. Найдем функцию проводимости схемы:
Решение. Имеется
четыре возможных пути прохождения тока при замкнутых переключателях a,
b, c, d, e : через переключатели a, b; через переключатели a, e, d; через переключатели c, d и через переключатели c, e, b. Функция проводимости F(a, b, c, d, e) = a . b v a . e . d v c . d v c . e . b.
Слайд 51
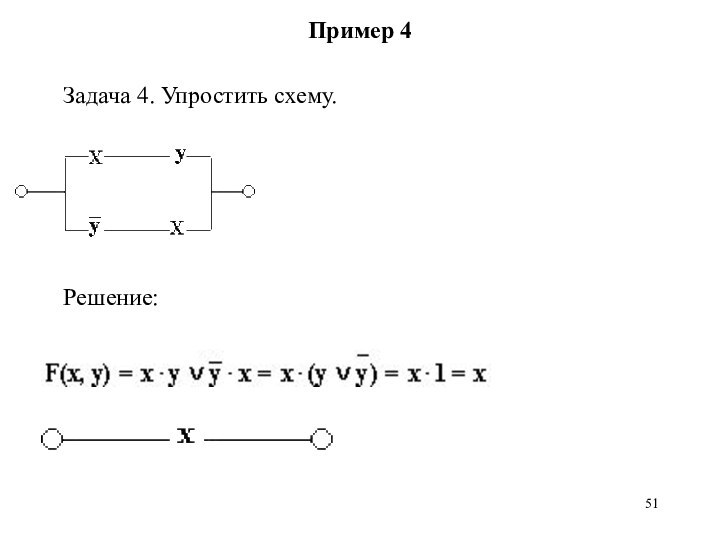
Пример 4
Задача 4. Упростить схему.
Решение:
Слайд 52
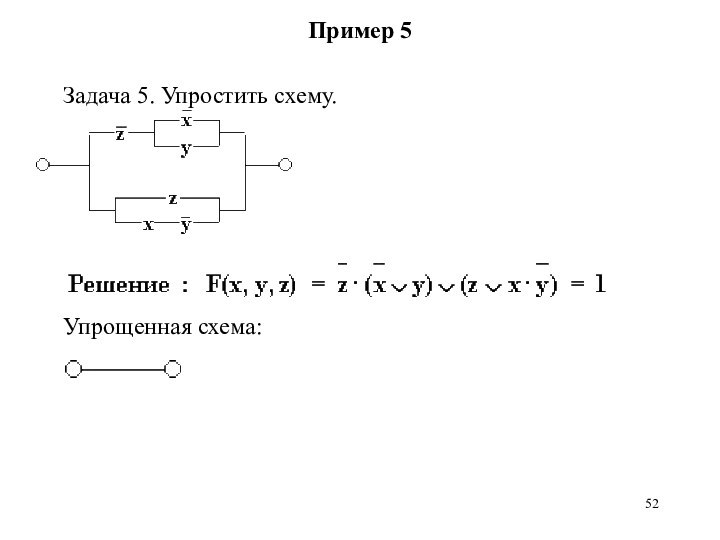
Пример 5
Задача 5. Упростить схему.
Упрощенная схема:
Слайд 53
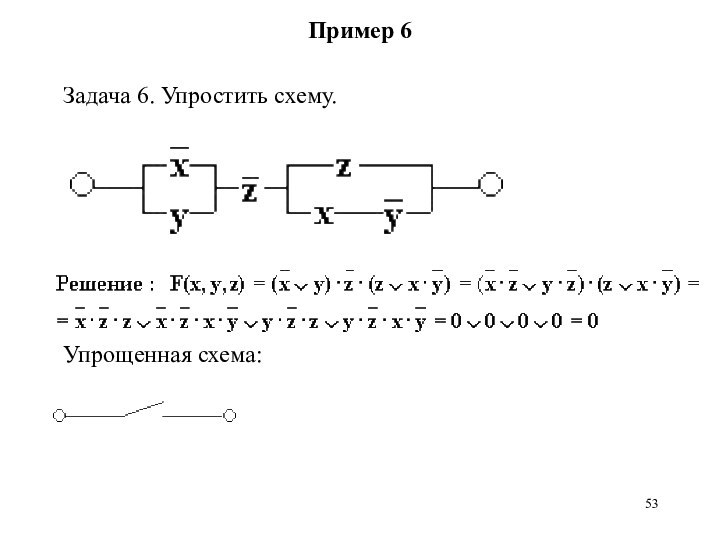
Пример 6
Задача 6. Упростить схему.
Упрощенная схема:
Слайд 54
Пример 7
Задача 7. Упростить схему.
Упрощенная схема:
Слайд 55
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ КОМПЬЮТЕРА
Логический элемент компьютера — это
часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.
Логическими
элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.
Слайд 56
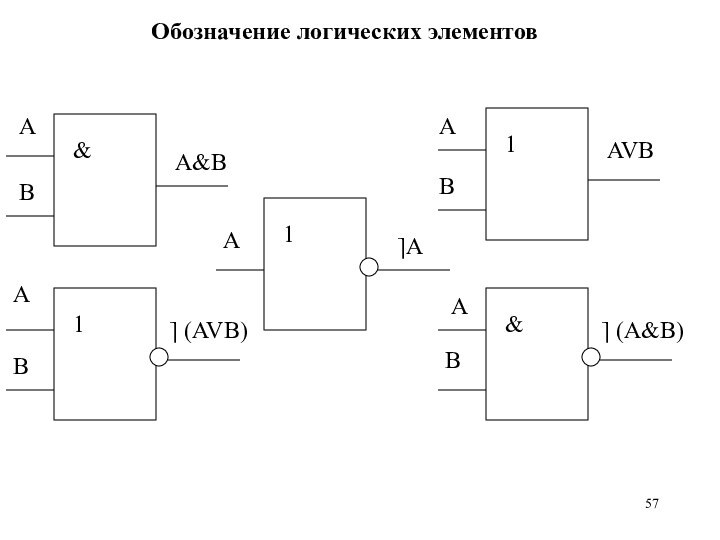
ФУНКЦИИ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
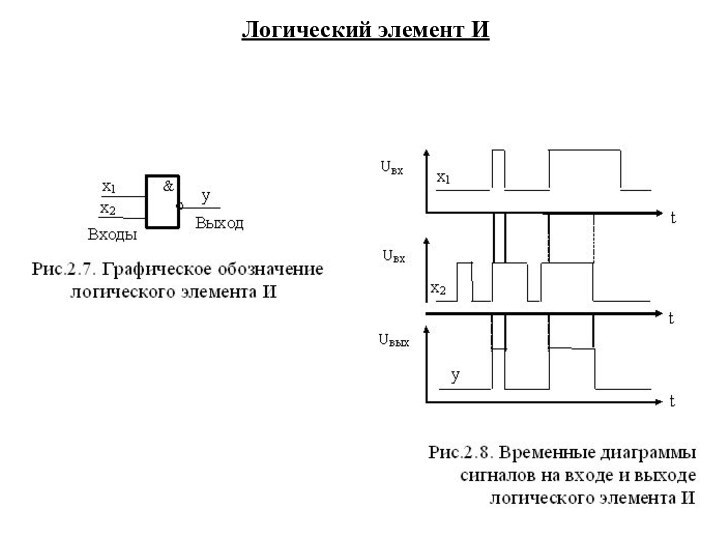
Схема «И» реализует операцию логического умножения
двух или более логических значений.
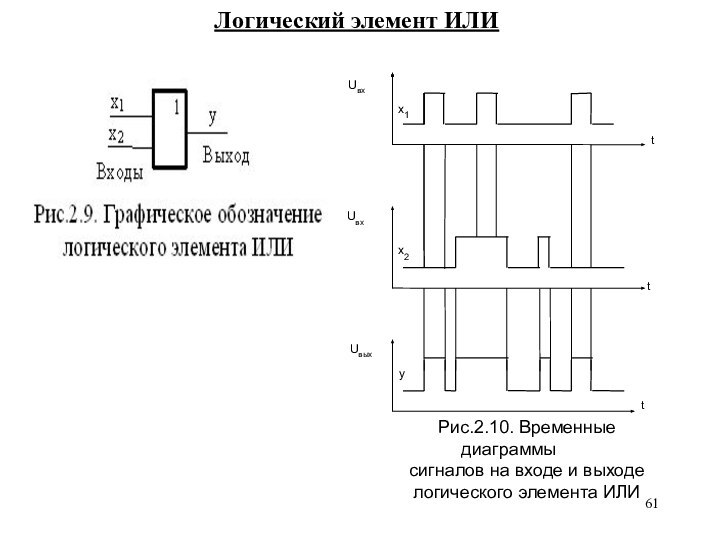
Схема
«ИЛИ» реализует логическое сложение двух или более логических значений.
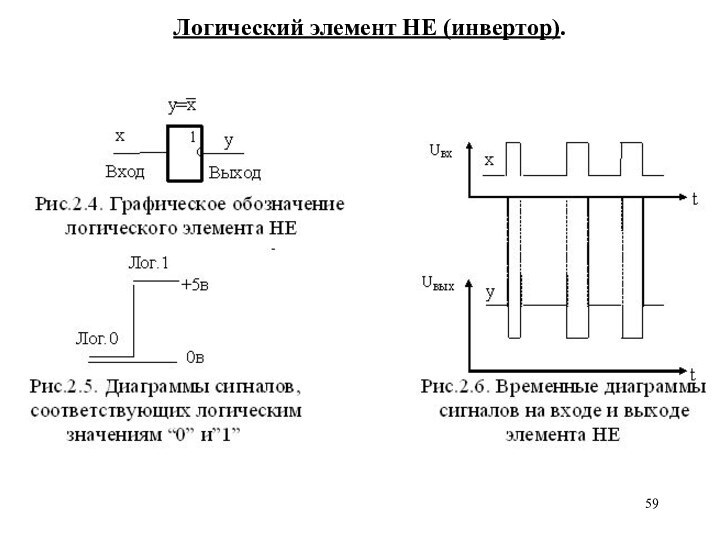
Схема «НЕ» реализует логическое отрицание логического значения.
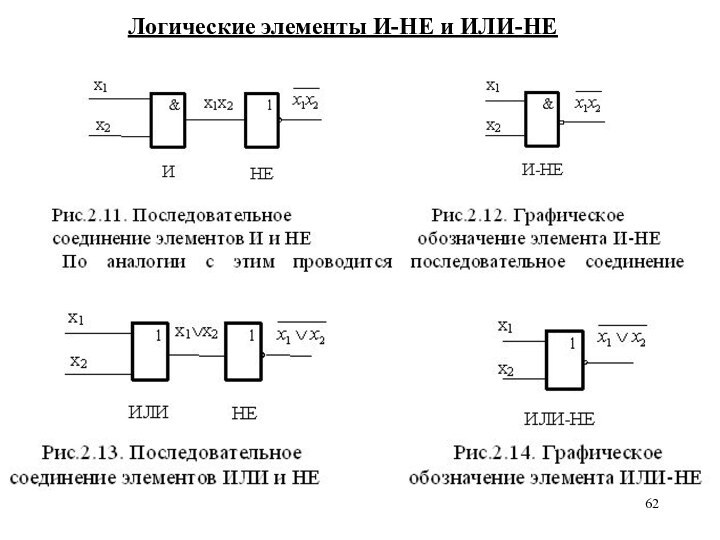
Схема «И-НЕ» реализует отрицание результата схемы «И».
Схема «ИЛИ-НЕ» реализует отрицание схемы «ИЛИ».
Слайд 57
Обозначение логических элементов
Слайд 58
Построение электронной схемы по логическому выражению
Найдем группу операций
одного типа выполняемых в последнюю очередь. Обозначим количество операций
группы через k.
Выберем логический элемент. Соответствующий логическим операциям группы.
Свяжем с выходом логического элемента результат логического выражения.
Определим количество входов логического элемента.
Установим порядок выполнения логических операций.
Удалим из исходного логического выражения операции найденной группы.
Сопоставим каждому полученному выражению один из входов выбранного логического элемента.
Слайд 59
Логический элемент НЕ (инвертор).
Слайд 61
Логический элемент ИЛИ
Рис.2.10. Временные диаграммы
сигналов на
входе и выходе
логического элемента ИЛИ
Слайд 62
Логические элементы И-НЕ и ИЛИ-НЕ
Слайд 63
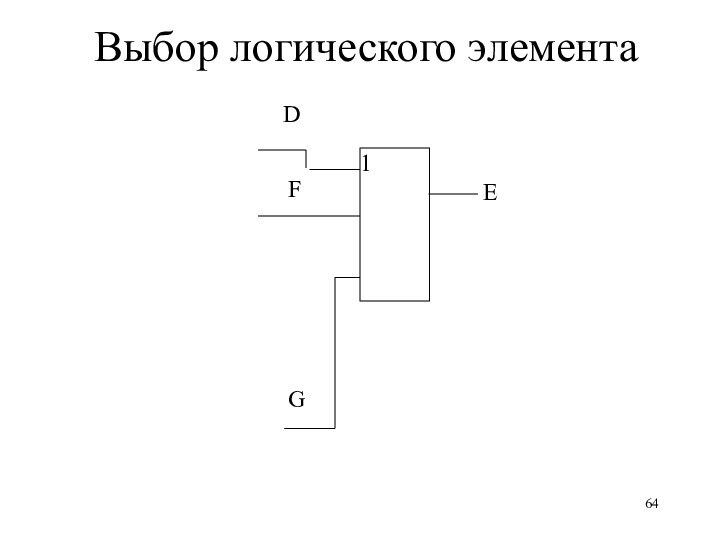
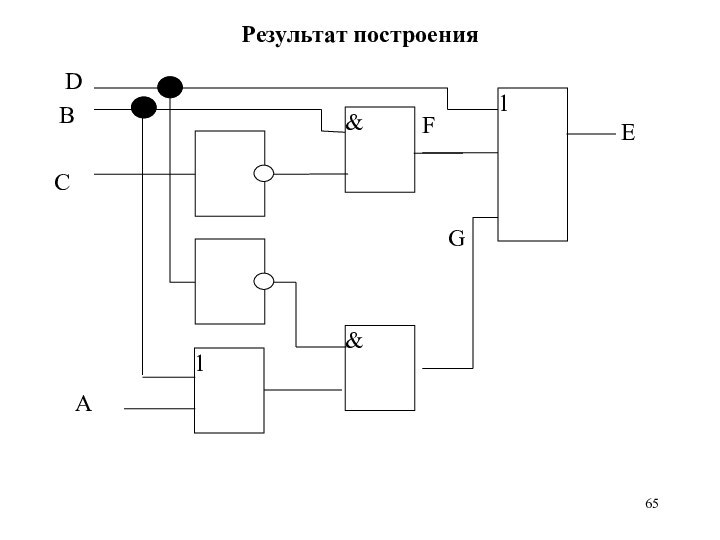
ПРИМЕР ПОСТРОЕНИЯ ЭЛЕКТРОННОЙ СХЕМЫ
Исходное логическое выражение:
E = D
+ B⋅⎤ С + ⎤ D⋅(A + B),
E =
D + F+ G,
Разбиение исходного выражения:
D
F = B⋅⎤ С,
G= ⎤ D⋅(A + B).
Слайд 66
Триггеры – элементы памяти цифровых автоматов, в
свою очередь являются элементарными цифровыми автоматами (автоматами Мура) с
двумя устойчивыми состояниями.
Слайд 67
Основные типы триггеров
триггер с раздельной установкой состояний (RS-триггер),
триггер "защелка" (D - триггер),
универсальный триггер (JK - триггер),
триггер
со счетным входом (T - триггер)
Слайд 68
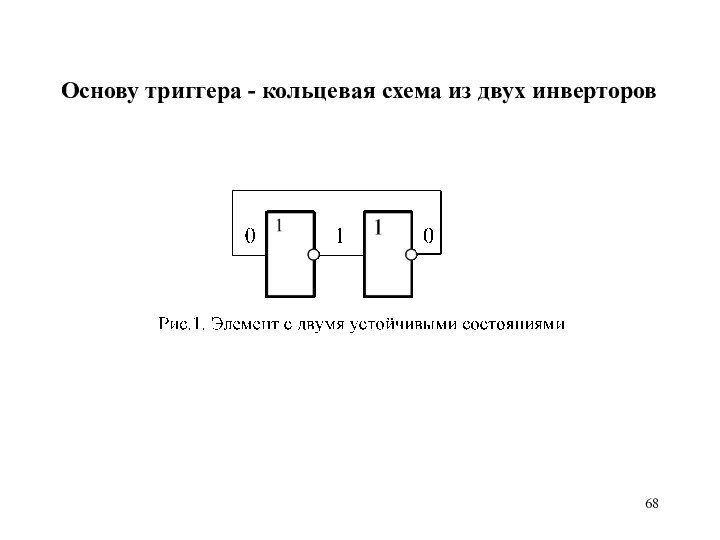
Основу триггера - кольцевая
схема из двух инверторов
Слайд 69
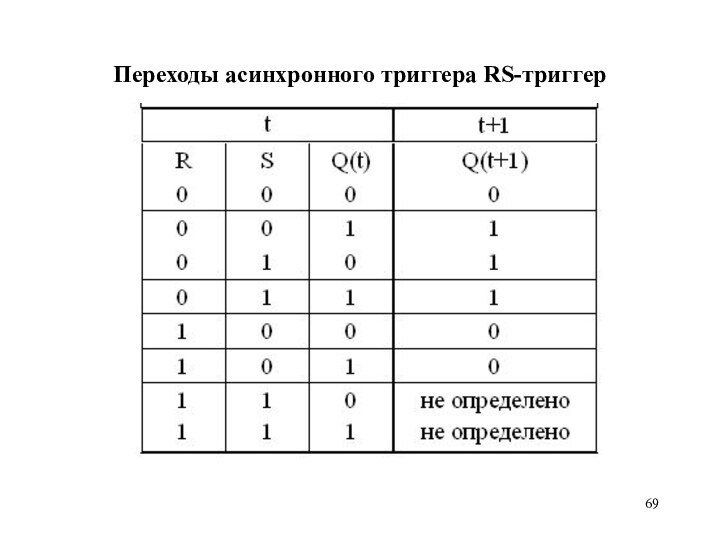
Переходы асинхронного триггера RS-триггер
Слайд 70
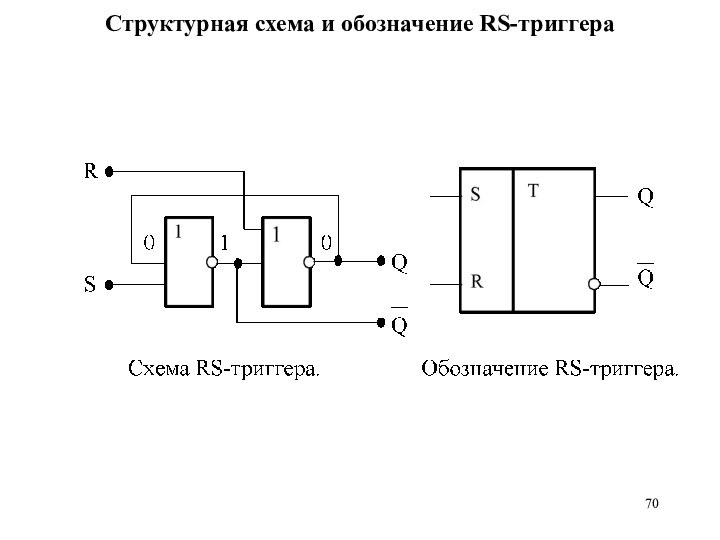
Структурная схема и обозначение RS-триггера
Слайд 71
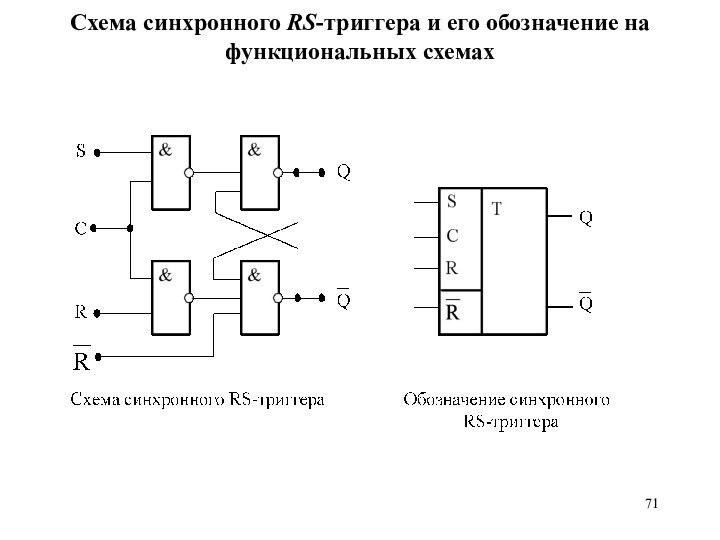
Схема синхронного RS-триггера и его обозначение на функциональных
схемах
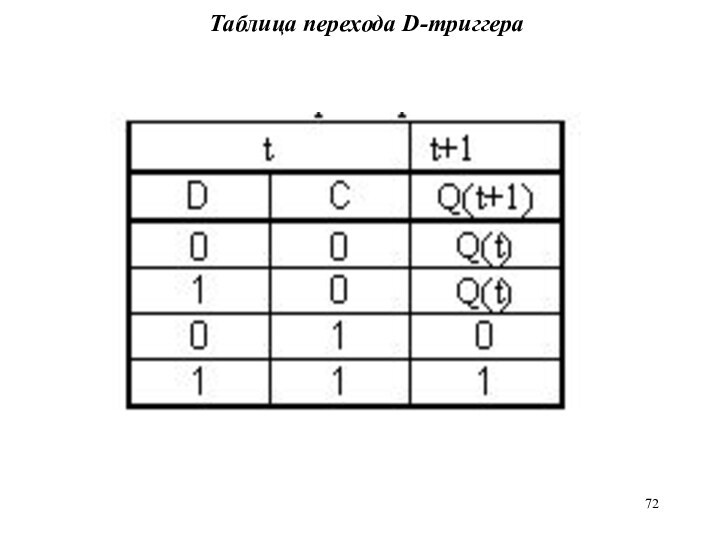
Слайд 73
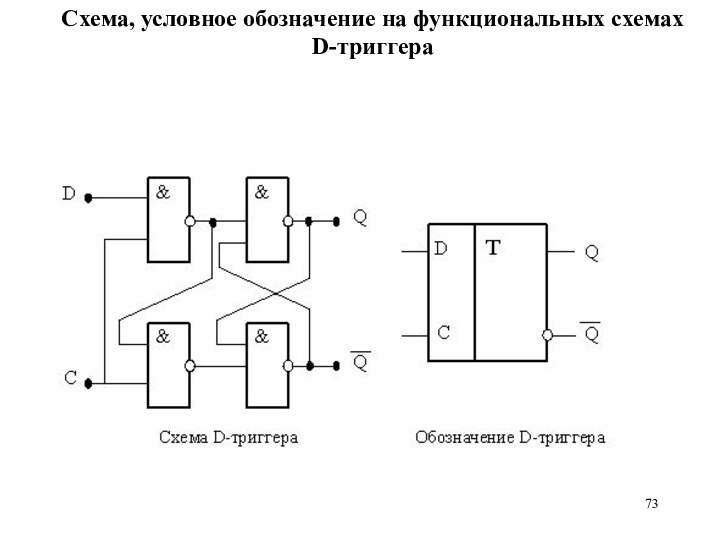
Схема, условное обозначение на функциональных схемах D-триггера
Слайд 74
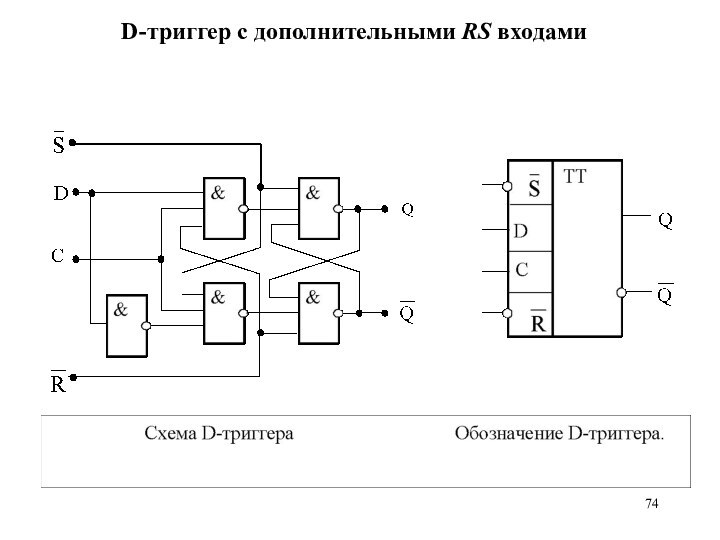
D-триггер с дополнительными RS входами
Слайд 75
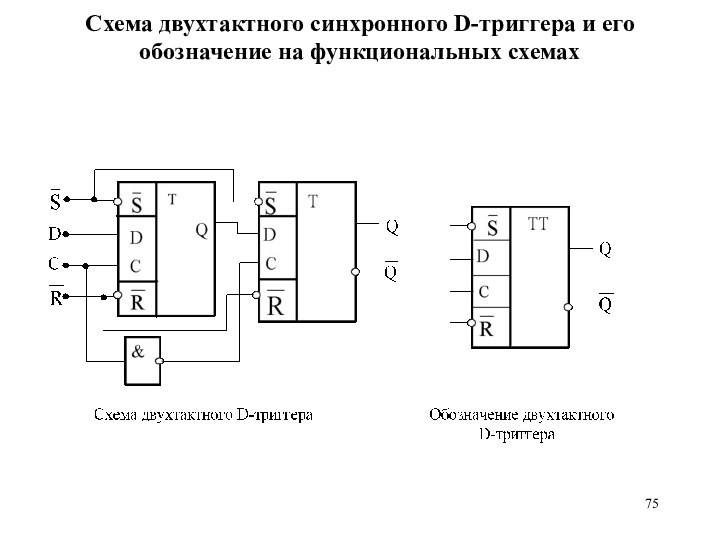
Схема двухтактного синхронного D-триггера и его обозначение на
функциональных схемах
Слайд 76
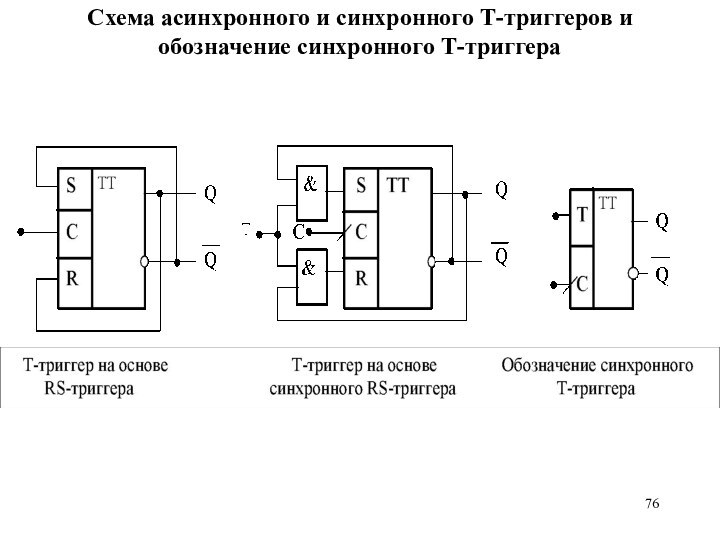
Схема асинхронного и синхронного Т-триггеров и обозначение синхронного
Т-триггера
Слайд 77
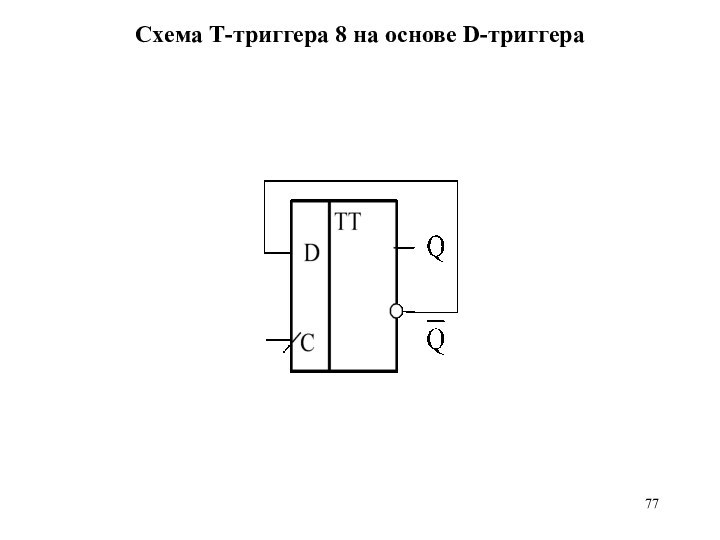
Схема Т-триггера 8 на основе D-триггера
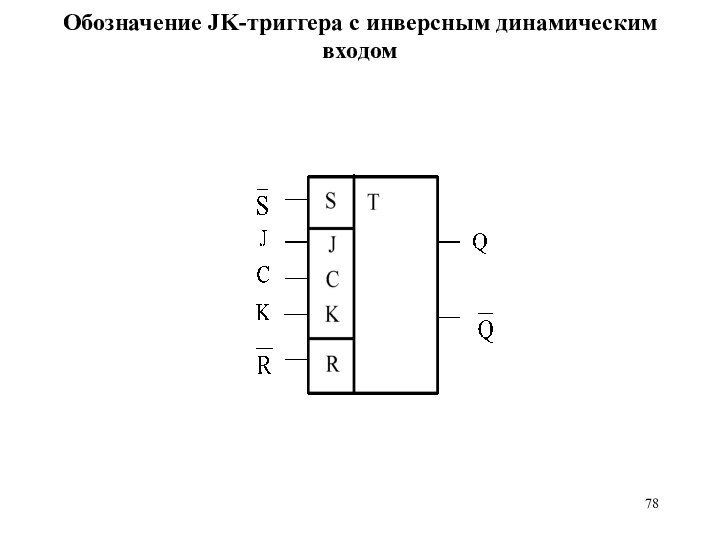
Слайд 78
Обозначение JK-триггера с инверсным динамическим входом
Слайд 79
Вопросы по лекции
В чем отличие конечного автомата от
комбинационных схем?
Как различаются автоматы Мура и Мили?
Сколько состояний имеет
элементарный автомат?
Что такое триггер?
Почему Т-триггер называют триггером со счетным входом?
В какое состояние перейдет Т-триггер при входном сигнале Т = 1?
Какая запрещенная комбинация входных сигналов для RS-триггера?
В какое состояние перейдет RS-триггер при сигнале S = 1?
В какое состояние перейдет JK -триггер при сигнале К = 1?
В какое состояние перейдет JK -триггер при сигнале J = K = 1?