Слайд 2
Понятие M-файла
Как повторно ввести серию команд
?
Два способа:
1.
Использовать окно Command History
2. Применить m-файл
m-файл может содержать команды,
а также управляющие
структуры языка MatLab.
Вызов такого файла осуществляется заданием его имени.
Имя этого файла должно иметь расширение m.
Это текстовый файл – можно создавать и редактировать
в любом текстовом редакторе (предпочтительнее – во
встроенном редакторе MatLab).
m-файлы подразделяются на 2 типа:
сценарии (script)
функции (function)
Слайд 3
M-файл (сценарий)
Содержит серию команд, которые выполняются в
режиме
интерпретации построчно.
Если в команде имеется ошибка, она не обрабатывается,
и система переходит в режим ожидания.
Сценарий работает только с переменными, расположенными в рабочей области MatLab.
М-функция
Отличие от сценария:
Функция может компилироваться целиком с последующим размещением исполняемого кода в памяти
Функция может иметь локальные переменные, размещаемые в собственной рабочей области
В функции могут быть входные и выходные параметры
Слайд 4
Синтаксис определения и вызова
М-функций
Текст М- функции должен
начинаться с заголовка, после которого следует тело функции. Заголовок
имеет следующий вид:
function [Ret1,Ret2,….]=fName(par1,par2,…)
где Ret1,Ret2,… – выходные параметры,
par1,par2,… – входные параметры
Например :
function Ret1=f1(par1,par2)
function [Ret1,Ret2,Ret3]=f2(par1)
Указанное в заголовке имя функции должно совпадать с именем файла, расширение имени файла должно быть m.
Слайд 5
Тело функции состоит из инструкций на m-языке, с
помощью которых вычисляются возвращаемые значения
function ret1=myFunc(x1,x2)
% myFunc calculates
x1*x2
% plus x1^2 +2x1 +3
%------------------------------------
ret1=x1.*x2 +AnotherFunc(x1);
Изнутри данного m-файла могут вызываться другие функции
function ret2 = AnotherFunc(y)
ret2=y.*y + 2*y +3;
Справка, содержащаяся в нескольких верхних строках комментария выдается по команде
>>help myFunc
myFunc calculates x1*x2
plus x1^2 +2x1 +3
Вызывать функцию из командного окна (или другого m-файла ) можно, задав её имя с фактическими параметрами
Слайд 6
Особенности графики системы MATLAB
Для визуализации вычислений используются
графические объекты, создаваемые на принципах дескрипторной (описательной) графики
Иерархическая структура
объектов дескрипторной графики строится на принципах объектно-ориентированного программирования и состоит из 4-х уровней, связанных по принципу «родитель-потомок»:
root (корень) — первичный объект, соответствующий экрану компьютера
figure (рисунок) — объект создания графического окна
координатные оси, меню, панели инструментов и т.д.
растровые изображения, линии, тексты и т.д.
Большинство команд высокоуровневой графики автоматически устанавливает свойства графических объектов и обеспечивает воспроизведение графики в нужных системе координат, палитре цветов, масштабе и т. д. ( т.е ориентировано на конечного пользователя-непрограммиста)
Слайд 7
Основы графической визуализации вычислений
sin(x)
Слайд 8
Построение графика функций одной переменной
Пусть интервал изменения
аргумента х от 0 до 10 с шагом 0.1
Для построения графика sin(x) достаточно задать вектор
х=0:0.1:10
а затем команду построения графиков plot(x,sin(x))
График строится как кусочно-линейная функция по узловым точкам
Слайд 9
Построение в одном окне графиков нескольких функций
Можно
воспользоваться функцией вида
plot(a1,f1,a2,f2,a3,f3,...)
где al, а2, аЗ,… —
векторы аргументов функций
f1, f2, f3,... — векторы значений функций
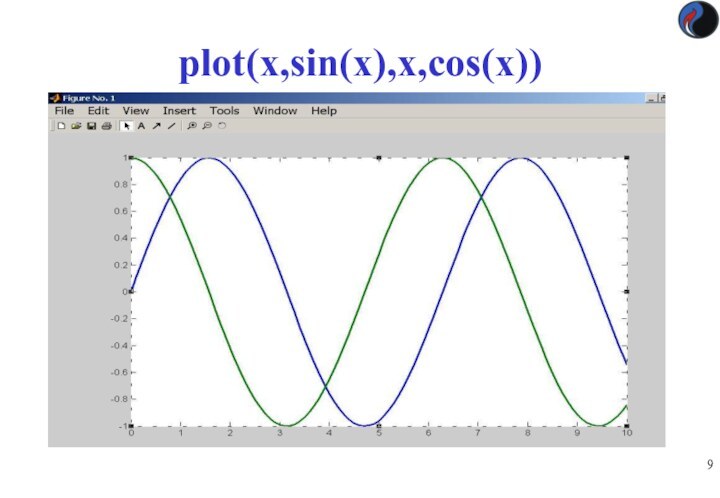
Чтобы построить в одном окне графики sin и cos: plot(x,sin(x),x,cos(x))
Другой вариант:
plot(x,sin(x)) ; hold on; plot(x,cos(x))
hold on позволяет удержать содержимое графического окна
Слайд 11
Разбиение графического окна
subplot( m,n,k ) – позволяет
разбить область вывода графической информации на несколько подобластей, в
каждую из которых можно вывести графики различных функций
m-равно числу строк подобластей,
n- числу колонок подобластей,
k - номеру подобласти , в которую выводится график (подобласти нумеруются слева направо по строкам)
Пример
x=-15:0.1:15;
subplot(2,2,1),plot(x,sin(x))
subplot(2,2,2),plot(sin(5*x),cos(2*x+0.2))
subplot(2,2,3),plot(x,cos(x).^2)
subplot(2,2,4),plot(x,sin(x)./x)
Слайд 13
Характеристики линии
В общем случае функция построения графика: plot(x,y,S)
где строковая константа S задаёт тип линии
Слайд 14
plot(x,y1,'-m', x,y2,'-.+r‘, х,у3,'--ok')
Слайд 15
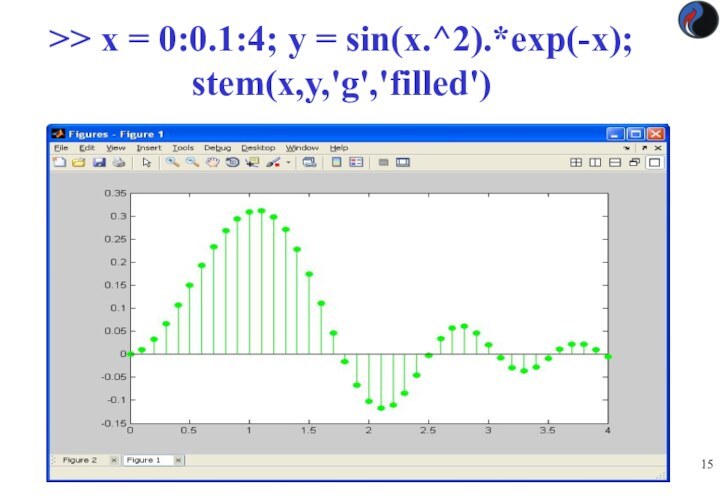
График дискретных отсчётов функции
Можно строить график функции
у(х) по дискретным отсчётам. Этот вид графика применяется, например,
при квантовании сигналов. Каждый отсчет представляется вертикальной чертой с кружком stem(Y) — строит график функции с ординатами в векторе Y (по оси абсцисс - количество отсчетов)
stem(X,Y) — строит график отсчетов с ординатами в векторе Y и абсциссами в векторе X
stem(.... 'filled') — график с закрашенными кружками
stem(.... 'LINESPEC') — 'LINESPEC‘ - спецификация линий, аналогичная приведенной для функции plot
Слайд 16
>> x = 0:0.1:4; y = sin(x.^2).*exp(-x); stem(x,y,'g','filled')
Слайд 17
Графики в полярной системе координат
В полярной системе координат
любая точка представляется как конец радиус-вектора, исходящего из начала
системы координат, имеющего длину r и угол phi. Для построения графика функции в полярной системе координат используется функция вида
polar(phi,r,s)
где s - строковая константа, задающая тип линии
Слайд 18
phi=0:0.01:2*pi; r=5*cos(2-7*phi);
polar(phi,r)
Слайд 19
Круговые диаграммы
Круговая диаграмма (функция pie(x)) показывает, какой процент
от суммы всех элементов составляет конкретный элемент. pie3 -
объёмная диаграмма
>>x=[3,7,1,2];
>>pie(x)
Слайд 20
Столбцовые диаграммы
Если Y – матрица, имеющая m
строк и n столбцов, то
bar(Y) строит m групп n
вертикальных столбиков по значениям элементов матрицы Y
Что будет, если Y – вектор?
barh (Y) – столбики будут расположены горизонтально
bar(Y,width) — задаёт ширину столбиков
По умолчанию width = 0.8
При width > 1 столбики в группах перекрываются
При использовании спецификации 'stacked' в функции
bar(Y, 'stacked' )
все n столбиков в каждой из m групп строятся друг на друге
bar3 и bar3h строят 3-мерные bar-диаграммы
Слайд 21
y=[1 2 3; 4 5 6; 7 8
9]; bar(y)
Слайд 24
Построение гистограмм
hist(Y,M) - строит гистограмму в
виде столбцовой диаграммы, характеризующей число попаданий значений элементов вектора
Y в каждый из М интервалов
hist(Y) – по умолчанию M= 10 интервалов
Если Y — матрица, строится гистограмма для каждого из её столбцов
hist(Y,X) - строит гистограмму для интервалов, центры которых заданы элементами вектора X
N=hist(Y,…) - возвращает число попаданий элементов вектора Y в заданные интервалы
Слайд 26
Угловые гистограммы
Применяются в индикаторах радиолокационных станций, для отображения
«роз ветров» и при построении других специальных графиков. Гистограмма
строится в полярной системе координат по данным вектора Y:
rose(Y) - для 20 интервалов
rose(Y, N) — для N интервалов
Интервалы - при изменении угла от 0 до 2*рi
rose(Y, X) - со спецификацией интервалов, указанной в векторе X
Слайд 28
Контурные графики
Используются в топографии для представления на
плоскости объемного рельефа местности с помощью линий равного уровня.
Они получаются, если трехмерная поверхность пересекается рядом плоскостей, расположенных параллельно друг другу
Контурный график представляет собой совокупность спроецированных на плоскость линий пересечения поверхности плоскостями
contour(Z,N) — строит контурный график по матрице Z с заданием N линий равного уровня (по умолчанию N=10)
Слайд 30
Трехмерная графика
Трехмерные поверхности – это функции двух переменных
z(x, у)
Построение поверхности состоит из 5-ти этапов
1. Задание
векторов значений аргументов x и y
2. Формирование двумерных массивов с информацией об узлах сетки, на которой строится поверхность – функция meshgrid
3. Вычисление в узлах сетки соответствующих значений функции z(x, у)
4. Вызов графика на экран - функция plot3
5. Отображение на графике дополнительной информации
Слайд 31
Функция meshgrid
>>x=[1 2 3]; y=[4 5 6]; [X,Y]=meshgrid(x,y)
X
= Y=
1 2
3 4 4 4
1 2 3 5 5 5
1 2 3 6 6 6
[X,Y] = meshgrid(x,y) — преобразует область, заданную векторами х и у, в массивы X и Y, определяющие сетку для вычисления функции двух переменных. Строки массива X - копии вектора х; а столбцы Y — копии вектора у.
x=-2:0.1:2; y=-4:0.2:4;
[X,Y]=meshgrid(x,y);
Z=-2*X.*exp(-X.^2-Y.^2); plot3(X,Y,Z)
Слайд 33
[X,Y]=meshgrid(-3:0.15:3);
Z=X.^2+Y.^2; plot3(X,Y,Z,'o')
Слайд 34
Та же поверхность, построенная функцией mesh(X,Y,Z)
Слайд 35
meshc(X,Y,Z) строит поверхность с линиями равного уровня, спроектированными
на плоскость x,y
.
Слайд 36
meshz(X,Y,Z) – поверхность с перпендикулярами, опущенными из
граничных точек поверхности на плоскость.
Слайд 37
С помощью surf(X,Y,Z) можно построить каркасную поверхность, каждая
клетка которой закрашивается определенным цветом
Слайд 38
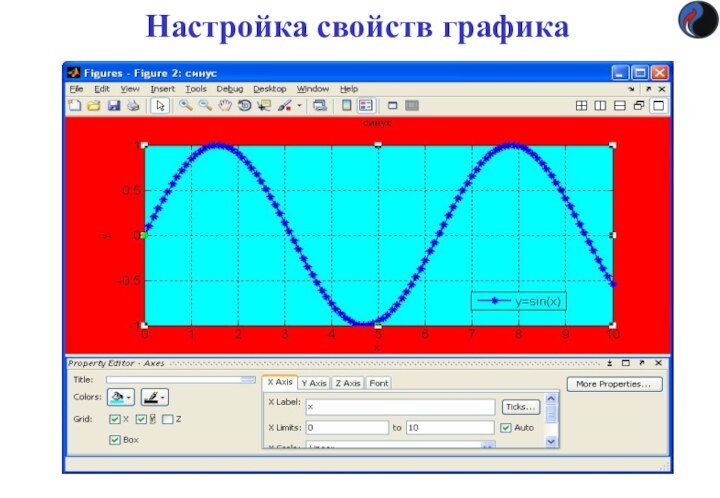
Оформление графиков
title('string ') — установка титульной надписи, заданной
строковой константой 'string'
Функции установки названий осей х, у и
z :
xlabel('string') ; ylabel('string') ; zlabel('string')
Размещение текста в произвольном месте рисунка :
text(x,y, 'string') — выводит текст в точку с координатами (x,y)
text(x,y,z, 'string') — выводит текст в точку с координатами (x,y,z)
gtext('string') — выводит текст, который можно установить мышью в нужное место графика
Установка диапазонов координат :
axis([XMIN XMAX YMIN YMAX]) — по осям х и у для текущего двумерного графика
axis([XMIN XMAX YMIN YMAX ZMIN ZMAX]) - по осям х, у и z для текущего трехмерного графика
Слайд 39
Вывод легенды
legend(‘stringl’,’string2’, ...,Pos) — помещает легенду в место,
определённое параметром Pos:
Pos = 0 — выбирается автоматически
Pos
= l — верхний правый угол
Pos = 2 — верхний левый угол
Pos = 3 — нижний левый угол
Pos = 4 — нижний правый угол
Pos = -l — справа от графика
Можно и без Pos.
С помощью мыши легенду легко перетащить в любое другое место
Слайд 40
Вывод координатной сетки
grid on — добавляет сетку к
текущему графику;
grid off — отключает сетку;
grid —
последовательно производит включение и отключение сетки
Слайд 41
Дополнительные параметры форматирования графиков
(…,'LineWidth',5) – ширина линии
5
(…,’FontSize’,14) – размер шрифта 14
(…,’MarkerSize’,8) – размер маркера 8
Все
рассмотренные ранее функции сами раскрывают окно figure 1
Закрыть текущее окно можно командой close
Команда figure(2) раскрывает второе окно и т.д. Закрыть – close 2
Все окна сразу закрываются командой close ALL
С помощью команды get можно вывести значения параметров графика, а командой set можно изменить эти значения
Пример
>> figure(2)
>> x=0:0.1:10;
>> y=sin(x);
>> hPlot=plot(x,y,'-*');
>> set(hPlot,'LineWidth',2,'MarkerSize',8);
>> get(hPlot)
Слайд 42
Интерактивное редактирование графиков
В меню окна построенного графика
опции
Edit, Insert и Tools позволяют легко управлять параметрами графиков
Можно
также воспользоваться возможностями
панели инструментов
Слайд 43
Изменение масштаба графика
Инструмент Лупа
+ увеличивает вдвое
–
уменьшает вдвое
Перемещая мышь при
нажатой левой клавише,
можно выделить область
детализации; после
отпускания клавиши эта
область отобразится во
всё окно


















![Понятие M-файла y=[1 2 3; 4 5 6; 7 8 9]; bar(y)](/img/tmb/15/1454817/310b3c56f4c98a47fa5b6d8684cb5192-720x.jpg)









![Понятие M-файла Функция meshgrid>>x=[1 2 3]; y=[4 5 6]; [X,Y]=meshgrid(x,y)X = Y= 1](/img/tmb/15/1454817/e469ff6a5670596cdab3387037896e38-720x.jpg)

![Понятие M-файла [X,Y]=meshgrid(-3:0.15:3); Z=X.^2+Y.^2; plot3(X,Y,Z,'o')](/img/tmb/15/1454817/f9d7bd23ab04c875e71f0cf2021e0ad6-720x.jpg)