НАД ЭЛЛИПТИЧЕСКИМИ КРИВЫМИ
Положения выносимые на защиту:
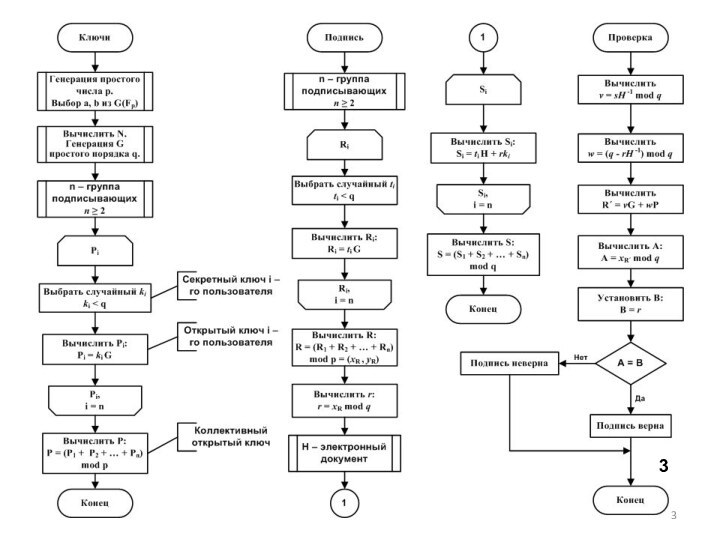
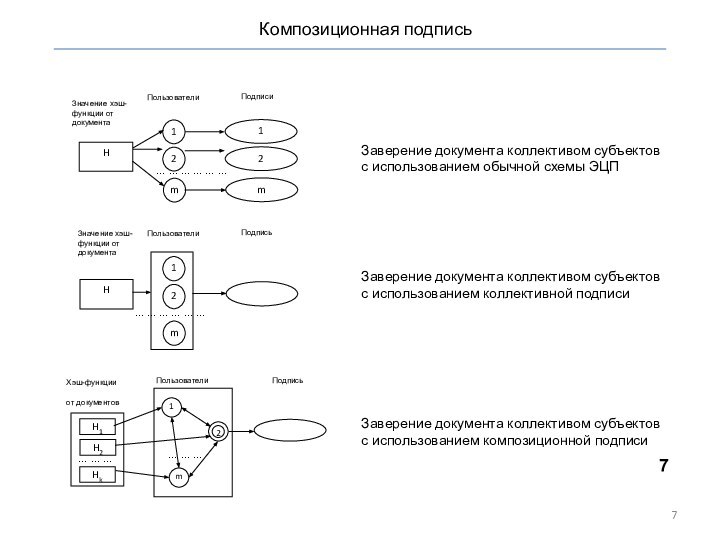
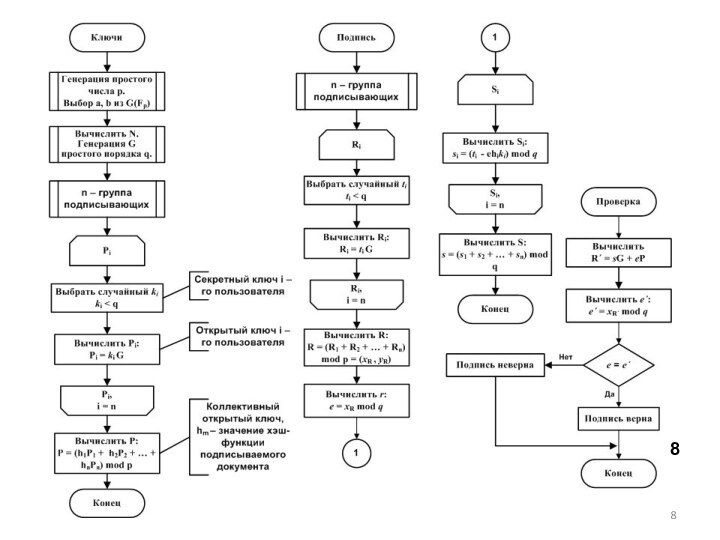
способ формирования коллективной ЭЦП,
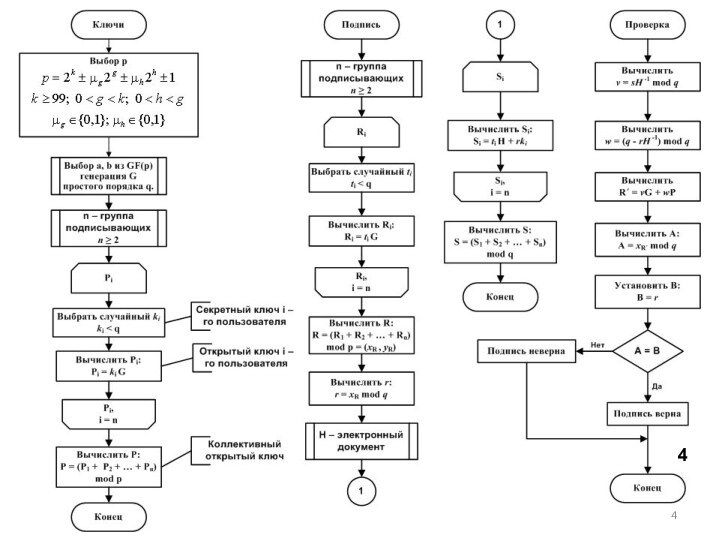
отличающийся обеспечением ее внутренней целостностипротокол коллективной ЭЦП, отличающийся сокращением вычислительной сложности процедур ее проверки и формирования
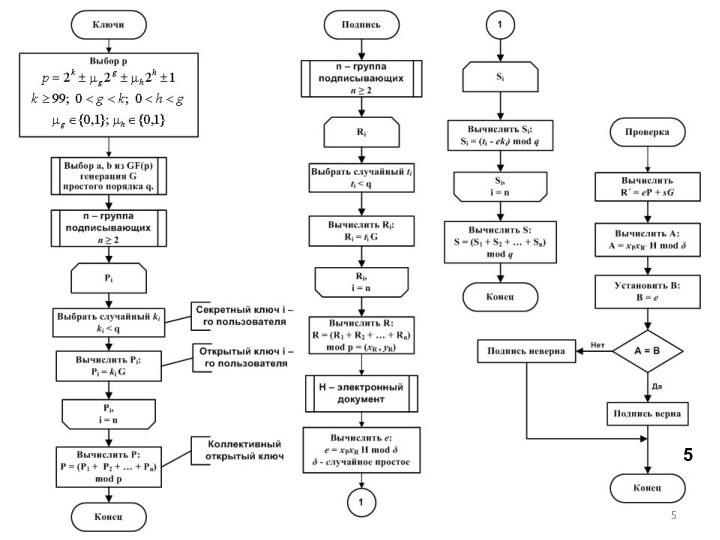
протокол композиционной ЭЦП, сокращающий ее размер для использования на бумажных носителях
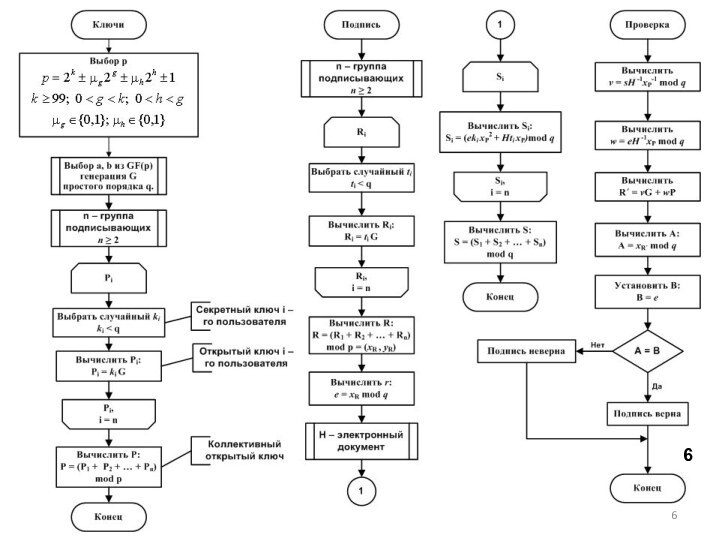
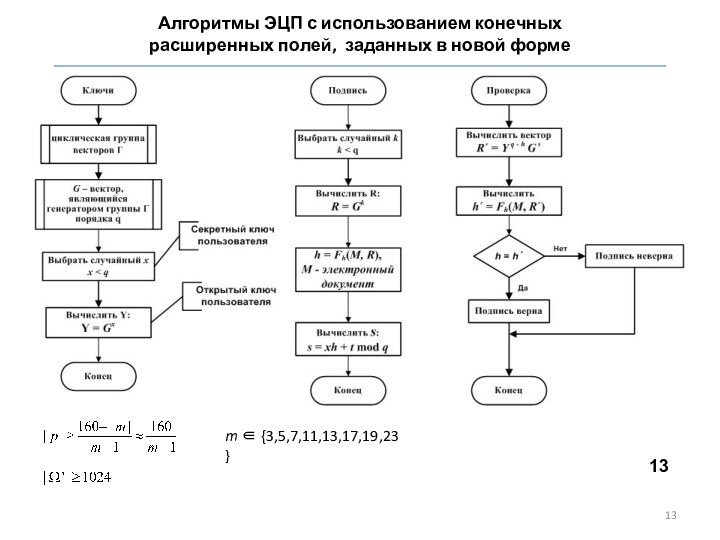
алгоритм построения ЭЦП, отличающийся использованием конечных векторных полей