- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Система счисления
Содержание
- 2. Ключевые словасистема счисленияцифраалфавитпозиционная система счисленияоснованиеразвёрнутая форма записи
- 3. Система счисления - это знаковая система для
- 4. Узловые числа обозначаются цифрами.Узловые и алгоритмические числаАлгоритмические
- 5. Простейшая и самая древняя система счисления -
- 6. Римская система счисления40=XL1935MCMXXX28XXVIIIVНепозиционная система счисленияСистема счисления называется
- 7. Система счисления называется позиционной, если значение цифры
- 8. Цифры 1234567890 сложились в Индии около 400
- 9. В позиционной системе счисления с основанием q
- 10. Aq = ±(an–1 qn–1 + an–2
- 11. Примеры записи чисел в развёрнутой форме:2015
- 12. Двоичная система счисленияДвоичной системой счисления называется позиционная
- 13. Двоичная система счисленияДвоичной системой счисления называется позиционная
- 14. Правило перевода целых десятичных чисел в двоичную
- 15. Перевод целых десятичных чисел в двоичную систему1)
- 16. 36310 = 101101011231410 = 1001110102Компактное оформлениеПравило перевода целых десятичных чисел в двоичную систему счисления
- 17. Пример: 10638 = 183 + 082 +
- 18. an–1an–2…a1a0 = an–18n–1+an–28n–2+…+a080Пример: 10638 = 183 +
- 19. Основание: q = 16.Алфавит: 0, 1, 2,
- 20. 1) последовательно выполнять деление данного числа и
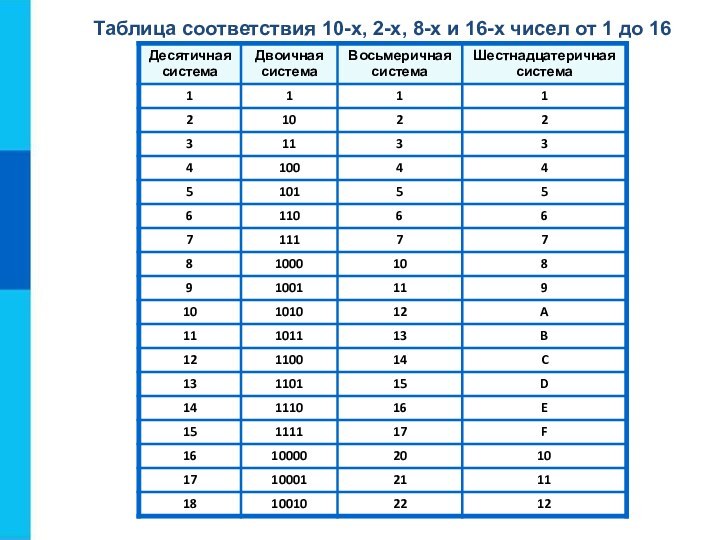
- 21. Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16
- 22. Двоичная арифметикаАрифметика двоичной системы счисления основывается на
- 23. «Компьютерные» системы счисленияДвоичная система используется в компьютерной
- 24. Система счисления — это знаковая система, в
- 25. Вопросы и заданияЧем различаются унарные, позиционные и
- 26. Опорный конспектНепозиционнаяВ позиционной системе счисления с основанием
- 27. Скачать презентацию
- 28. Похожие презентации



















![Система счисления Электронные образовательные ресурсыhttp://school-collection.edu.ru/catalog/res/caeea6cc-bd1d-4f47-9046-1434ac57e111/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – Умножение и деление двоичных чиселhttp://school-collection.edu.ru/catalog/res/402b749c-240b-4e16-9e4d-bea3fc4fa8fa/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – История развития](/img/tmb/13/1258797/9507db680d15c51b49058a6f63d00d91-720x.jpg)
Слайд 2
Ключевые слова
система счисления
цифра
алфавит
позиционная система счисления
основание
развёрнутая форма записи числа
свёрнутая
форма записи числа
Слайд 3 Система счисления - это знаковая система для записи
чисел при помощи определенного набора символов.
Цифры – это
знаки, при помощи которых записываются числа.Алфавит системы счисления – это совокупность цифр.
Общие сведения
Древнеславянская система счисления
Вавилонская система счисления
Египетская система счисления
Слайд 4
Узловые числа обозначаются цифрами.
Узловые и алгоритмические числа
Алгоритмические числа
получаются в результате каких-либо операций из узловых чисел.
100
+ 10 +
=
Слайд 5 Простейшая и самая древняя система счисления - унарная
система счисления. В ней для записи любых чисел используется
всего один символ - палочка, узелок, зарубка, камушек.Унарная система счисления
Узелковое письмо «кипу»
Зарубки
Примеры узлов «кипу»
Узелки, дощечки
Камушки
Слайд 6
Римская система счисления
40
=
X
L
1935
M
C
M
X
X
X
28
X
X
V
I
I
I
V
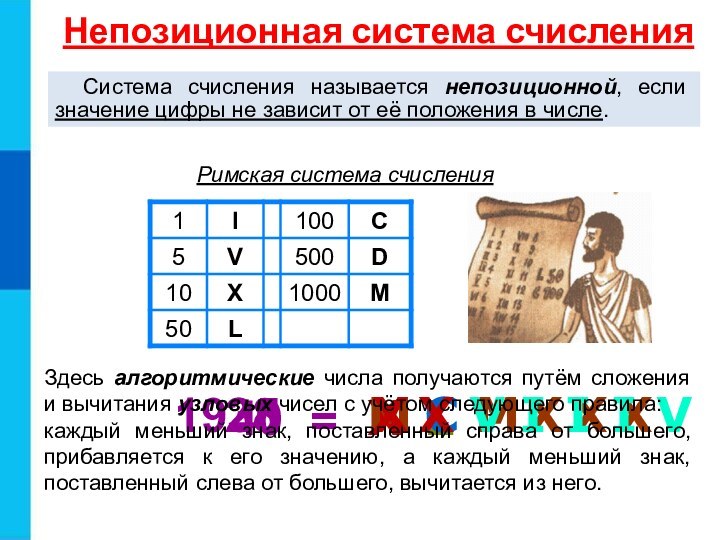
Непозиционная система счисления
Система счисления называется непозиционной,
если значение цифры не зависит от её положения в
числе.Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Слайд 7 Система счисления называется позиционной, если значение цифры зависит
от её положения в записи числа.
Одна и та же
цифра получает разные значения в зависимости от позиции, которую она занимает в записи числа.Основание позиционной системы счисления = количеству цифр, составляющих её алфавит.
Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Т.е. всего 10 цифр.
Следовательно, основание десятичной системы = 10
В десятичной системе десять единиц одного разряда составляют одну единицу старшего разряда
Позиционная система счисления
Слайд 8 Цифры 1234567890 сложились в Индии около 400 г.
н. э.
Арабы стали пользоваться подобной нумерацией около 800 г.
н. э.Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.
Десятичная система счисления
Слайд 9 В позиционной системе счисления с основанием q любое
число может быть представлено в виде:
Aq =±(an–1qn–1 + an–2
qn–2 +…+ a0 q0 + a–1q–1 +…+ a–m q–m) где:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутая форма.
Основная формула
Слайд 10 Aq = ±(an–1 qn–1 + an–2
qn–2 +…+ a0 q0 + a–1 q–1
+…+ a–m q–m)Примеры записи чисел в развёрнутой форме:
2015 = 2103 + 0102 + 1101 + 5100
0,125 = 110-1 + 210-2 + 510–3
14351,1 = 1104 + 4103 + 3102 + 5101 + 1100 + 110–1
Развёрнутая форма записи числа:
Слайд 11
Примеры записи чисел в развёрнутой форме:
2015 =
2103 + 0102 + 1101 + 5100
0,125 = 110-1
+ 210-2 + 510–314351,1 = 1104 + 4103 + 3102 + 5101 + 1100 + 110–1
Развёрнутая форма записи числа:
Слайд 12
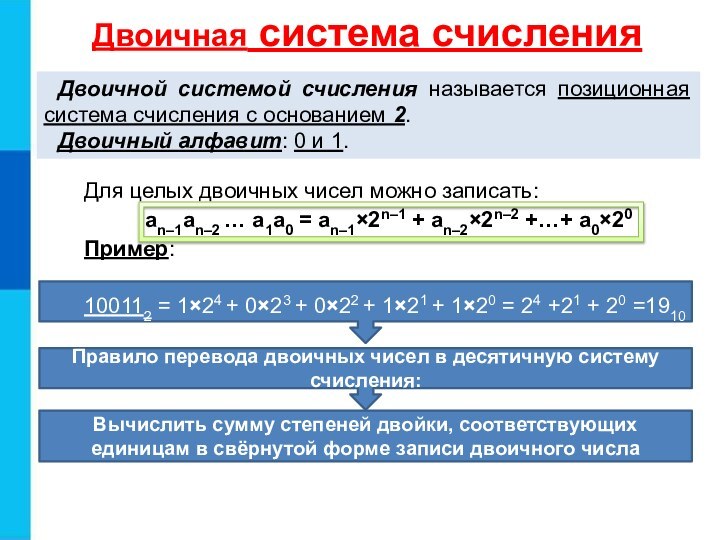
Двоичная система счисления
Двоичной системой счисления называется позиционная система
счисления с основанием 2.
Двоичный алфавит: 0 и 1.
Для целых
двоичных чисел можно записать:an–1an–2 … a1a0 = an–12n–1 + an–22n–2 +…+ a020
Пример:
100112 = 124 + 023 + 022 + 121 + 120 = 24 +21 + 20 =1910
Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа
Слайд 13
Двоичная система счисления
Двоичной системой счисления называется позиционная система
счисления с основанием 2.
Двоичный алфавит: 0 и 1.
100112 =
124 + 023 + 022 + 121 + 120 = 24 +21 + 20 =1910Правило перевода двоичных чисел в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа
Слайд 14 Правило перевода целых десятичных чисел в двоичную систему
счисления
an–12n–1+an–22n–2+… a121 +a0
= an–12n–2 +…+ a1 (остаток
a0)2
an–12n–1+an–22n–2+… a1
= an–12n–3+…+ a2 (остаток a1)
2
. . .
an–12n–1+an–22n–2+… a2
= an–12n–4 +…+ a3 (остаток a2)
2
На n-м шаге получим набор цифр: a0a1a2…an–1
Слайд 15
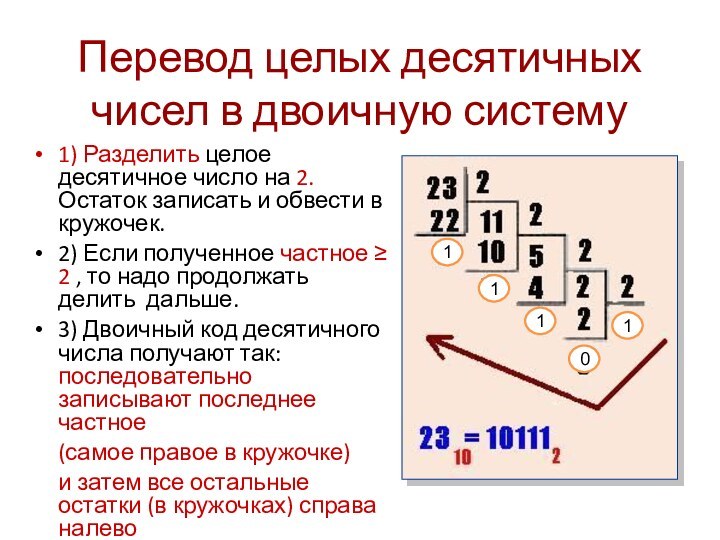
Перевод целых десятичных чисел в двоичную систему
1) Разделить
целое десятичное число на 2. Остаток записать и обвести
в кружочек.2) Если полученное частное ≥ 2 , то надо продолжать делить дальше.
3) Двоичный код десятичного числа получают так: последовательно записывают последнее частное
(самое правое в кружочке)
и затем все остальные остатки (в кружочках) справа налево
1
1
1
1
0
Слайд 16
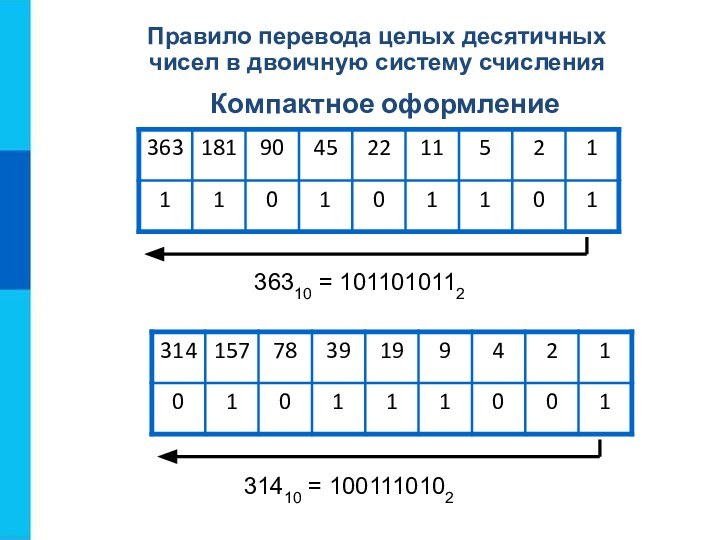
36310 = 1011010112
31410 = 1001110102
Компактное оформление
Правило перевода целых
десятичных чисел в двоичную систему счисления
Слайд 17 Пример: 10638 = 183 + 082 + 681+
380 = 56310
Для перевода целого восьмеричного числа в десятичную
систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.Восьмеричная система счисления
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Восьмеричной системой счисления называется позиционная система счисления с основанием q = 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Слайд 18
an–1an–2…a1a0 = an–18n–1+an–28n–2+…+a080
Пример: 10638 = 183 + 082
+ 681+ 380 = 56310
Для перевода целого восьмеричного числа
в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.Восьмеричная система счисления
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Восьмеричной системой счисления называется позиционная система счисления с основанием q = 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Слайд 19
Основание: q = 16.
Алфавит: 0, 1, 2, 3,
4, 5, 6, 7, 8, 9, A, B, C,
D, E, FШестнадцатеричная система счисления
Переведём десятичное число 154 в шестнадцатеричную систему счисления:
15410 = 9А16
154
16
9
144
10
(А)
16
Пример:
3АF16 = 3162 +10161 +15160 = 768 +160 +15 = 94310
Слайд 20 1) последовательно выполнять деление данного числа и получаемых
целых частных на основание новой системы счисления до тех
пор, пока не получим частное, равное нулю;2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Цифровые весы
Правило перевода целых десятичных чисел в систему счисления с основанием q
Слайд 22
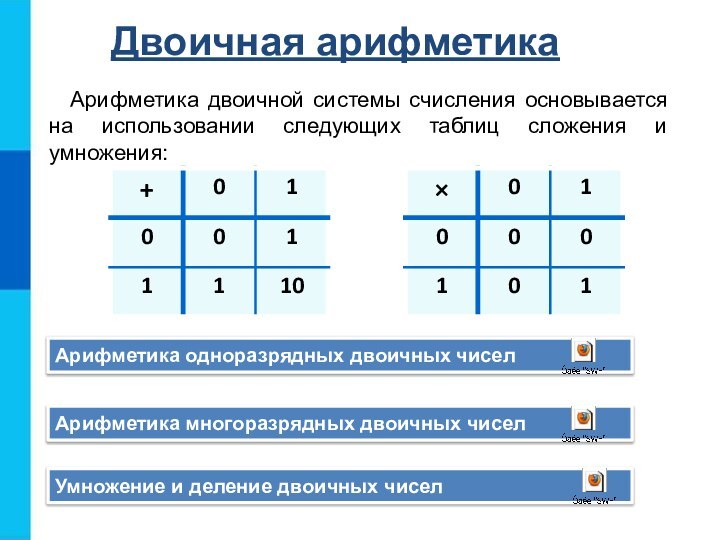
Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании
следующих таблиц сложения и умножения:
Арифметика одноразрядных двоичных чисел
Арифметика многоразрядных
двоичных чиселУмножение и деление двоичных чисел
Слайд 23
«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике,
так как:
двоичные числа представляются в компьютере с помощью простых
технических элементов с двумя устойчивыми состояниями;представление информации посредством только двух состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами.
Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.
Слайд 24 Система счисления — это знаковая система, в которой
приняты определённые правила записи чисел.
Система счисления называется позиционной,
если количественный эквивалент цифры в числе зависит от её положения в записи числа. В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq =±(an–1qn–1 + an–2qn–2 +…+ a0q0 + a–1q–1 +…+ a–mq–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Самое главное
Слайд 25
Вопросы и задания
Чем различаются унарные, позиционные и непозиционные
системы счисления?
Цифры каких систем счисления приведены на рисунке?
Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
Запишите в развёрнутом виде числа:
а) 143,51110
б) 1435118
в) 14351116
г) 1435,118
Запишите десятичные эквиваленты следующих чисел:
а) 1728
б) 2ЕА16
в) 1010102
г) 10,12
д) 2436
Укажите, какое из чисел 1100112, 1114,358 и1В16 является:
а) наибольшим
б) наименьшим
Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
Верны ли следующие равенства?
а) 334 =217
б) 338 =214
Найдите основание х системы счисления, если:
а) 14x=910
б) 2002x=13010
Переведите целые числа из десятичной системы счисления в двоичную:
а) 89
б) 600
в) 2010
Переведите целые числа из десятичной системы счисления в восьмеричную:
а) 513
б) 600
в) 2010
Переведите целые числа из десятичной системы счисления в шестнадцатеричную:
а) 513
б) 600
в) 2010
Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
Выполните операцию сложения над двоичными числами:
а) 101010 + 1101
б) 1010 + 1010
в) 10101 + 111
Выполните операцию умножения над двоичными числами:
а) 1010 · 11
б) 111 · 101
в) 1010 · 111
Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:
а) 1100 ? 11 ? 100 = 100000;
б) 1100 ? 10 ? 10 = 100;
в) 1100 ? 11 ? 100 = 0.
Вычислите выражения:
а) (11111012 +AF16):368
б) 1258 + 1012 ·2A16 – 1418
Ответ дайте в десятичной системе счисления.
Задачник «Системы счисления»
Слайд 26
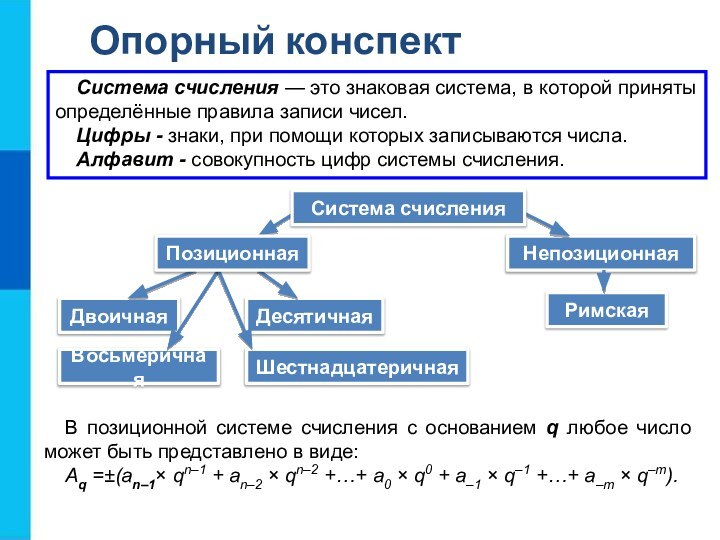
Опорный конспект
Непозиционная
В позиционной системе счисления с основанием q
любое число может быть представлено в виде:
Aq =±(an–1 qn–1
+ an–2 qn–2 +…+ a0 q0 + a–1 q–1 +…+ a–m q–m).Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит - совокупность цифр системы счисления.
Система счисления
Двоичная
Десятичная
Восьмеричная
Шестнадцатеричная
Римская
Позиционная