- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Таблицы истинности логических функций
Содержание
- 2. Таблицей истинности логической функции принято называть табличное
- 3. Таблица истинности функции логического отрицания (инверсии):
- 4. Таблица истинности функции логического сложения (дизъюнкции):
- 5. Свойства дизъюнкции:X ∨ Y ≡ Y ∨
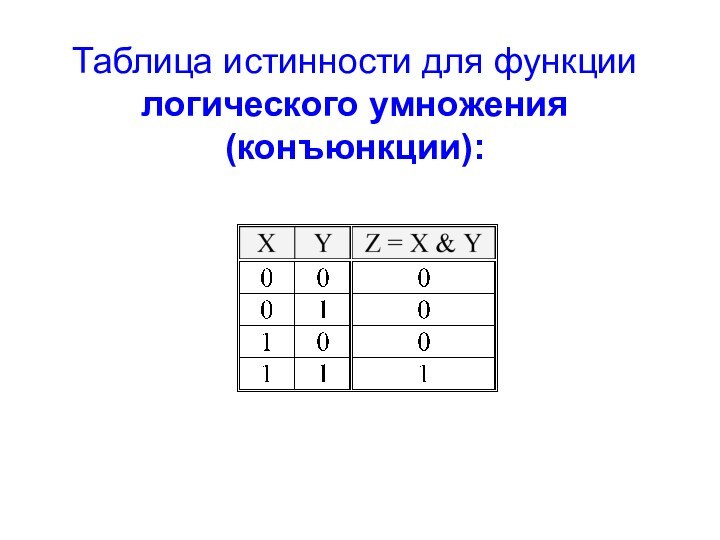
- 6. Таблица истинности для функции логического умножения (конъюнкции):
- 7. Свойства конъюнкции:X & X ≡ X;X &
- 8. Основные законы алгебры логики
- 11. Правила составления таблиц истинности для сложных логических
- 12. При построении таблиц истинности целесообразно придерживаться следующего
- 13. Затем строится таблица истинности с указанным количеством
- 14. Составление таблицы истинности для логической функции Z
- 15. Построим таблицу, подпишем столбцы и заполним ее
- 16. Скачать презентацию
- 17. Похожие презентации
Таблицей истинности логической функции принято называть табличное представление логической операции, в котором присутствуют все возможные сочетания значений входных переменных, и получаемые при этом значения выходных переменных (результатов логической операции).













Слайд 5
Свойства дизъюнкции:
X ∨ Y ≡ Y ∨ X;
(X
∨ Y) ∨ Z ≡ X ∨ (Y ∨
Z);X ∨ 0 ≡ X,
где 0 – тождественно ложное высказывание;
X ∨ X ≡ 1;
X ∨ 1 ≡ 1,
где 1 – тождественно истинное высказывание;
X ∨ X ≡ X
Слайд 7
Свойства конъюнкции:
X & X ≡ X;
X & Y
≡ Y & X;
(X & Y) & Z ≡
X & (Y & Z);X & X ≡ 0;
X & 0 ≡ 0;
где 0 – тождественно ложное высказывание
X & 1 ≡ X,
где 1 – тождественно истинное высказывание
Слайд 11 Правила составления таблиц истинности для сложных логических функций
Для любой логической функции можно построить таблицу истинности,
которая определяет
ее
истинность или ложность
при всех возможных комбинациях значений аргументов
(логических переменных).Слайд 12 При построении таблиц истинности целесообразно придерживаться следующего алгоритма
действий:
Сначала определяют количество строк в таблице истинности. Количество строк
будет равно 2n, (где n – количество логических переменных) плюс строка заголовка.Далее определяют количество столбцов в таблице истинности, оно равно количеству логических переменных плюс количество логических операций.
Слайд 13 Затем строится таблица истинности с указанным количеством строк
и столбцов, столбцы подписываются, в таблицу вносятся всевозможные наборы
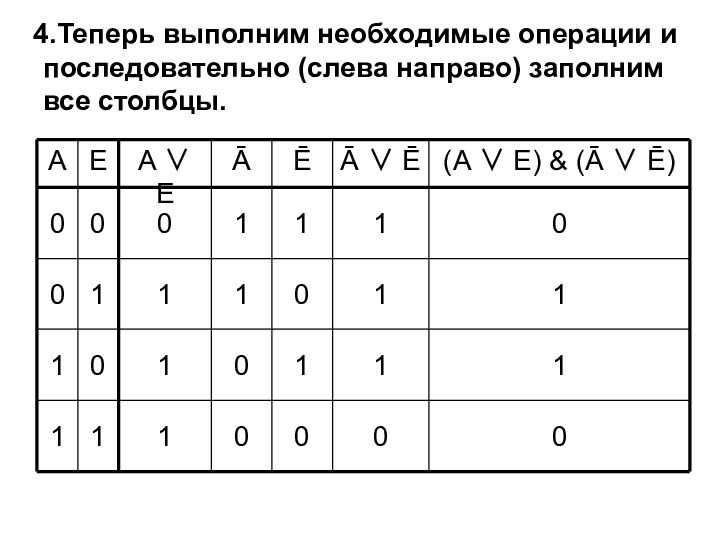
значений исходных логических переменных.И, наконец, выполняются необходимые логические операции, таблица истинности заполняется по столбцам.
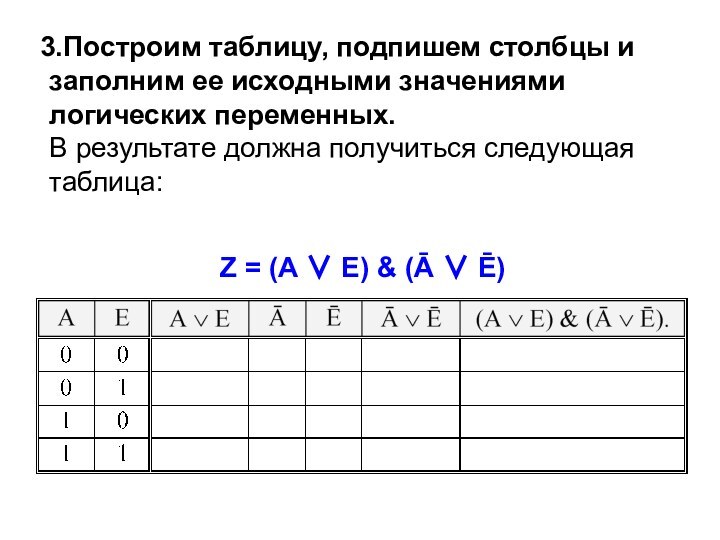
Слайд 14 Составление таблицы истинности для логической функции Z =
(A ∨ E) & (Ā ∨ Ē)
Определим количество строк
в нашей таблице истинности.Мы имеем две логические переменные А и Е, следовательно, количество строк будет равно 22 + 1 = 5.
Выясним, какое количество столбцов необходимо.
У нас – две логические переменные, над которыми будет выполнено 5 логических операций ‑ это A ∨ E, Ā, Ē, Ā ∨ Ē и, наконец (A ∨ E) & (Ā ∨ Ē). Значит, нам понадобится 7 столбцов.





























