Презентация на тему Законы алгебры логики

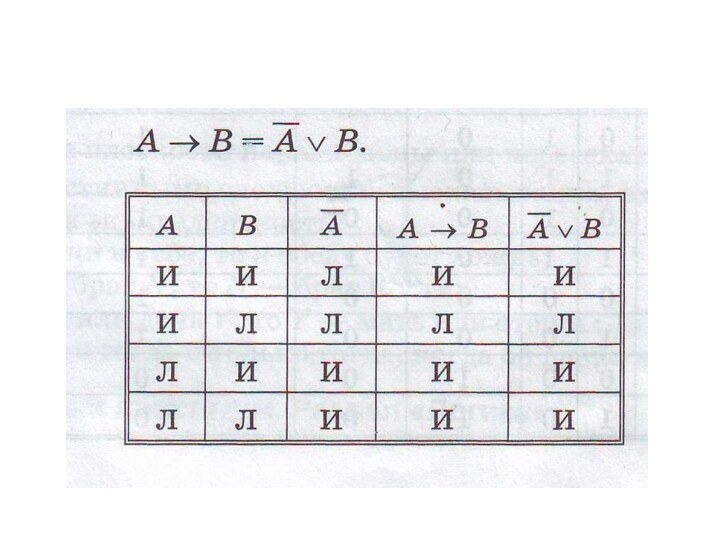
знаки логических операций.
Логическая функция – зависимость значения одной переменной

логической величины от других независимых логических величин аргументов.
Таблица истинности – перечень значений функции для всех сочетаний значений аргументов. Содержит 2 в степени n строк – где n число аргументов.

уравнение имеет действительные корни тогда и только тогда, когда

его дискриминант положительный.

2. Если квадратное уравнение имеет действительные корни, то его дискриминант положительный и если дискриминант квадратного уравнения положительный, то оно имеет действительные корни.

(1)
Соотношение (1) является тождеством двух логических формул.
Каким способом можно доказать справедливость равенства?

операцию эквивалентности к последовательности операций отрицания, дизъюнкции и конъюнкции.

к формуле, содержащей только операции отрицания, дизъюнкции и конъюнкции.
Такой

способ представления логической формулы называется нормальной формой.

Дмитрий. Относительно их умение играть в шахматы, справедливы следующие

высказывания:
Семен играет в шахматы
Если Виктор не играет в шахматы, то играет Семен и Дмитрий
Если Антон или Виктор играет, то Семен не играет.
Преобразуем эти высказывания к алгебраической форме. Введем логические переменные для обозначения четырех простых высказываний:
А = «Антон играет в шахматы»
В = «Виктор играет в шахматы»
С= «Семен играет в шахматы»
D = «Дмитрий играет в шахматы»