Презентация на тему Тела вращения

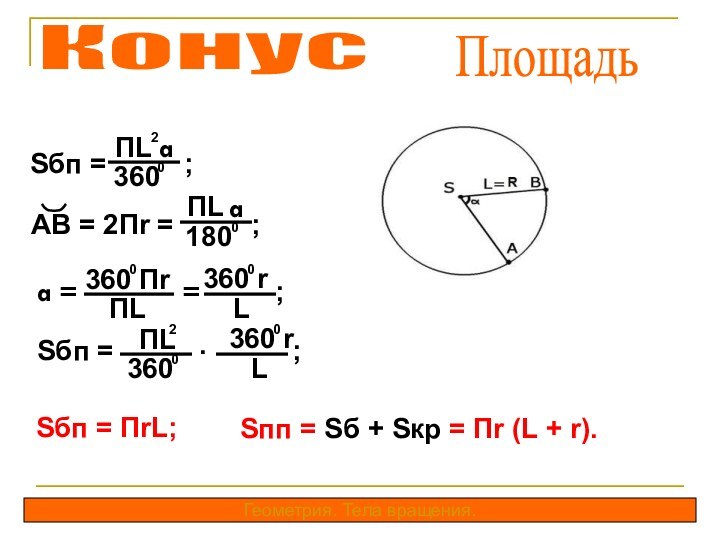
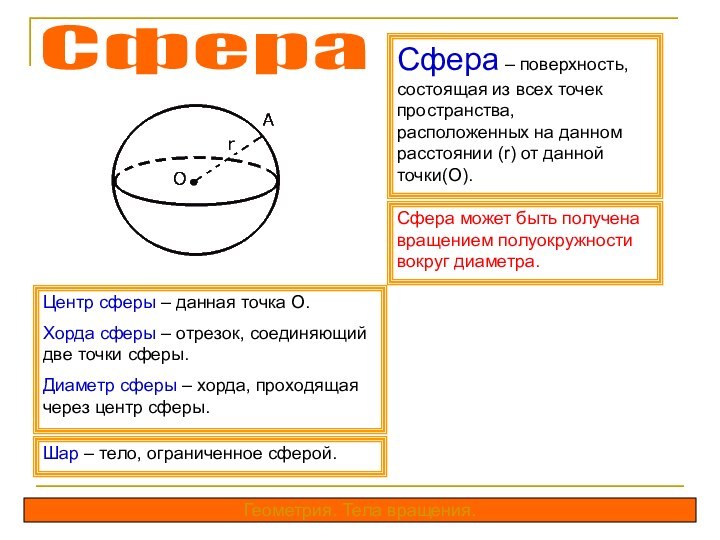
равных кругов, лежащих в параллельных плоскостях, и всех отрезков,

Основания кругового цилиндра – круги.

Образующие – отрезки, соединяющие соответствующие точки окружностей кругов.

Геометрия. Тела вращения.

цилиндр, образующие которого перпендикулярны основаниям.
Цилиндр может быть получен вращением

Радиус цилиндра – радиус его оснований.
Высота цилиндра – расстояние между плоскостями оснований.
Ось цилиндра – прямая, проходящая через центры оснований.

ось

высота

Цилиндр

Геометрия. Тела вращения.

2Sкр = 2Пrh + 2Пr = 2Пr(h + r).
2
Sпп

основания конуса, точки, не лежащей в плоскости основания, -

Образующие конуса – отрезки, соединяющие вершину конуса с точками окружности основания.

Геометрия. Тела вращения.

конус, у которого прямая, соединяющая его вершину с центром

Конус может быть получен вращением прямоугольного треугольника вокруг его катета.

Высота конуса – перпендикуляр,
опущенный из его вершины
на плоскость основания.
Ось прямого кругового конуса – прямая, содержащая его высоту.

ось

вершина

Конус

Геометрия. Тела вращения.

Тела вращения.
AB = 2Пr =

ПL

a

180

0

a = = ;

360 Пr

ПL

360 r

0

0

L

Sбп = ;

ПL

2

360

0

.

360 r

0

L

Sбп = ПrL;

Sпп = Sб + Sкр = Пr (L + r).

точек пространства, расположенных на данном расстоянии (r) от данной

Сфера может быть получена вращением полуокружности вокруг диаметра.

Центр сферы – данная точка О.
Хорда сферы – отрезок, соединяющий две точки сферы.
Диаметр сферы – хорда, проходящая через центр сферы.

Шар – тело, ограниченное сферой.

вращения.
Площадь