- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку повторения темы Окружность
Содержание
- 2. Свойство касательной.Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. АВ
- 3. Чем похожи и чем различаются углы АОВ
- 4. Отрезки касательных к окружности, проведенные из одной
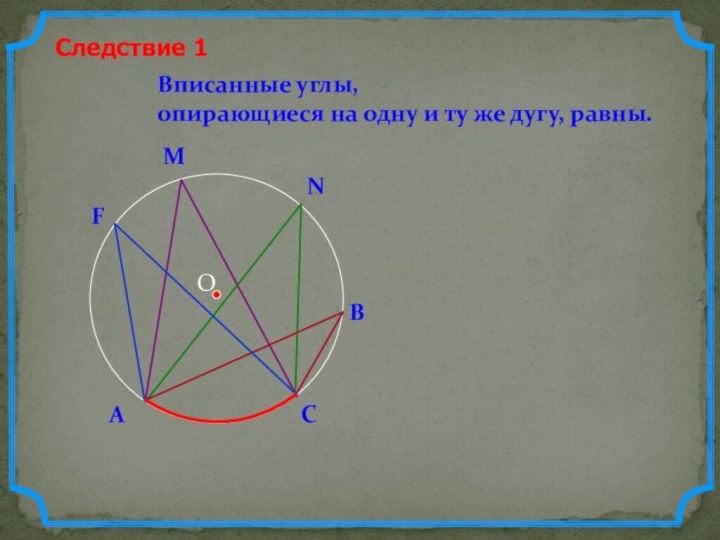
- 5. ОВписанные углы, опирающиеся на одну и ту же дугу, равны.Следствие 1ВNM
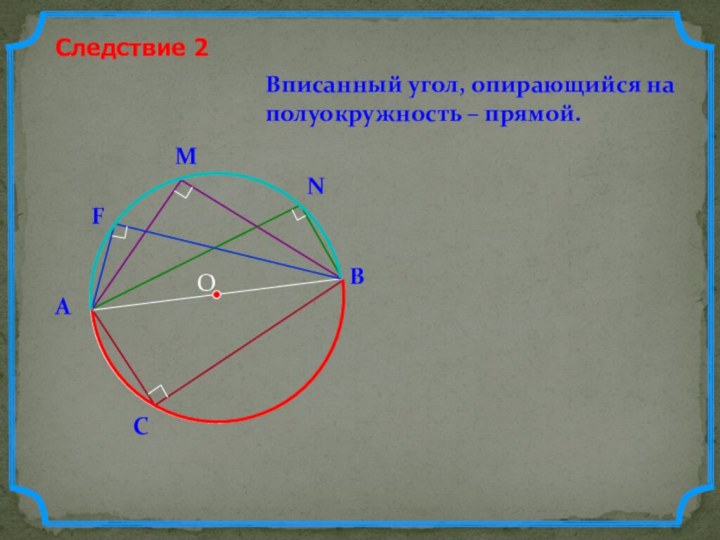
- 6. ОВписанный угол, опирающийся на полуокружность – прямой.Следствие 2ВА
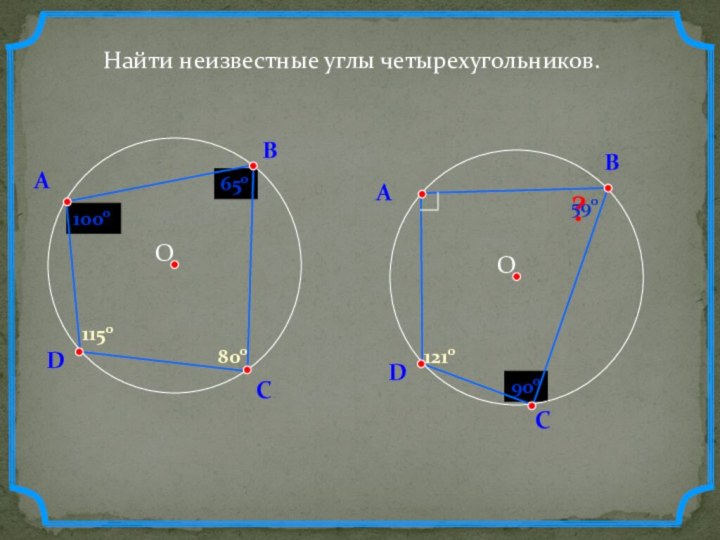
- 7. ?590?900?650?1000DАВС8001150DАВС1210Найти неизвестные углы четырехугольников.
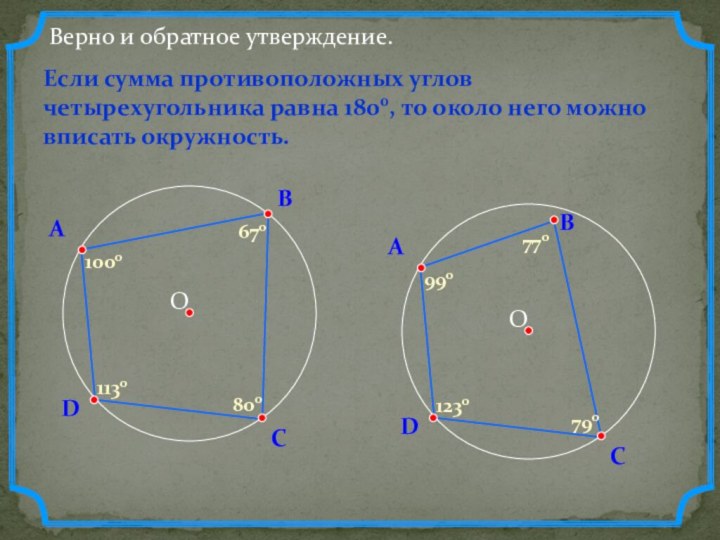
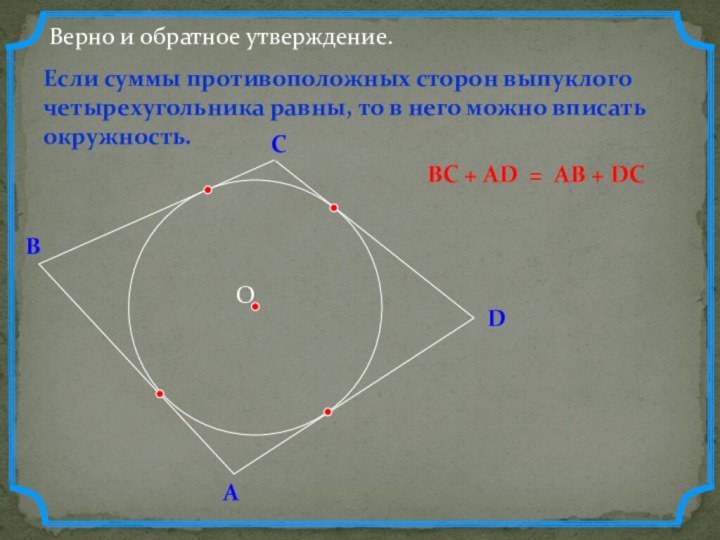
- 8. DВерно и обратное утверждение.Если сумма противоположных углов четырехугольника равна 1800, то около него можно вписать окружность.АВС80010001130670
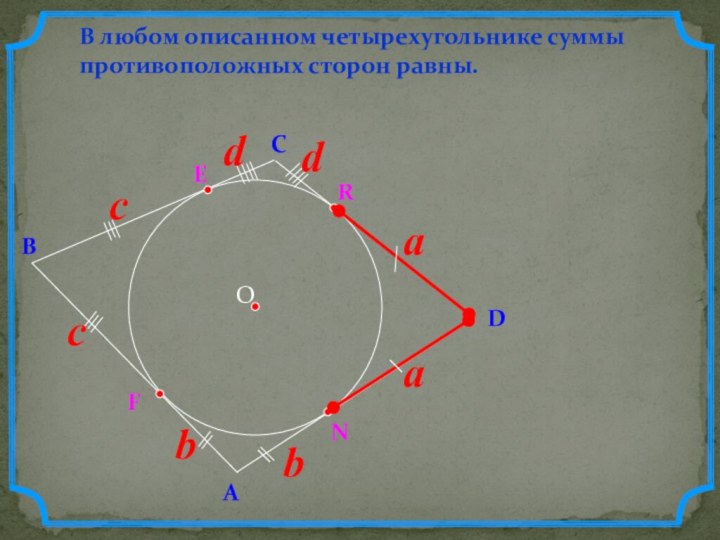
- 9. DВСВ любом описанном четырехугольнике суммы противоположных сторон равны.АERNF
- 10. Скачать презентацию
- 11. Похожие презентации
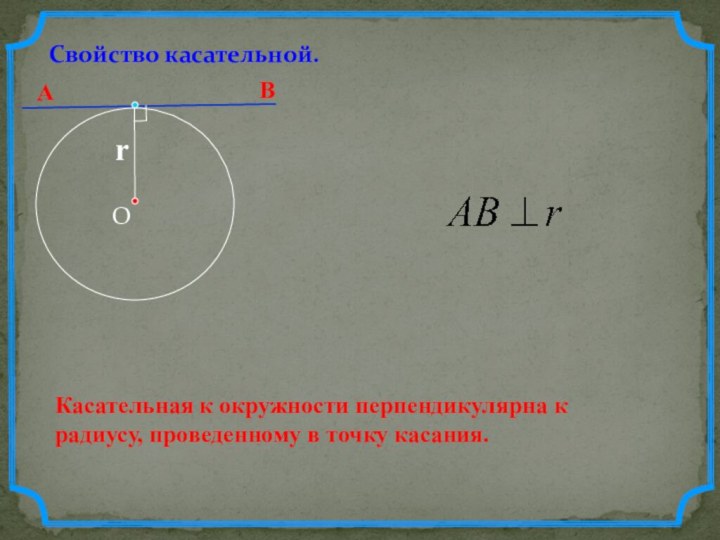
Свойство касательной.Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. АВ

Слайд 2
Свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному
в точку касания.
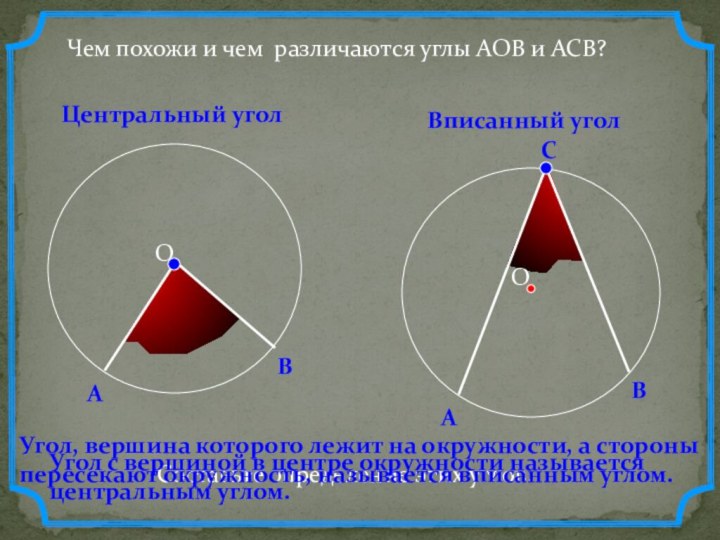
Слайд 3 Чем похожи и чем различаются углы АОВ и
АСВ?
Центральный угол
Вписанный угол
Составьте определение этих углов.
Угол с вершиной в
центре окружности называется центральным углом.Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
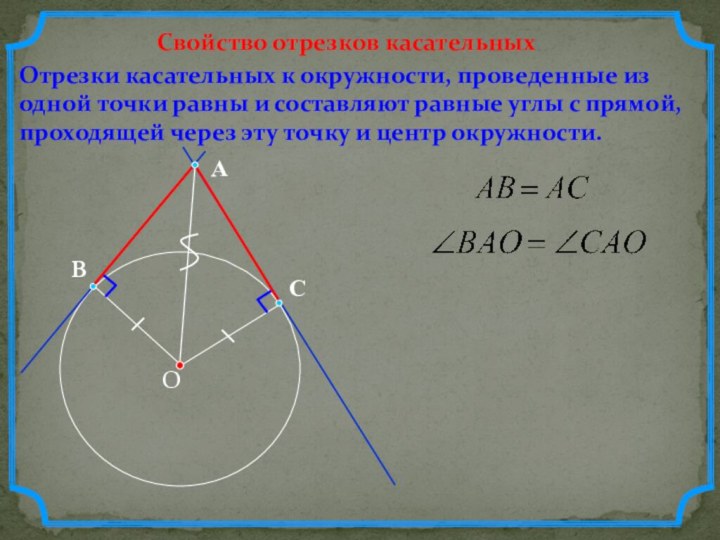
Слайд 4 Отрезки касательных к окружности, проведенные из одной точки
равны и составляют равные углы с прямой, проходящей через
эту точку и центр окружности.Свойство отрезков касательных





























