в районе
8 - в городе
11 – в крае.
2015-2016 уч.
год1 – в районе
6 – в городе
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть












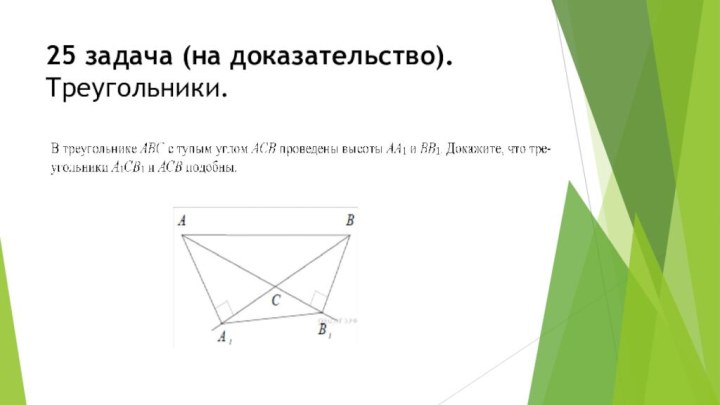









А
С
В
Н
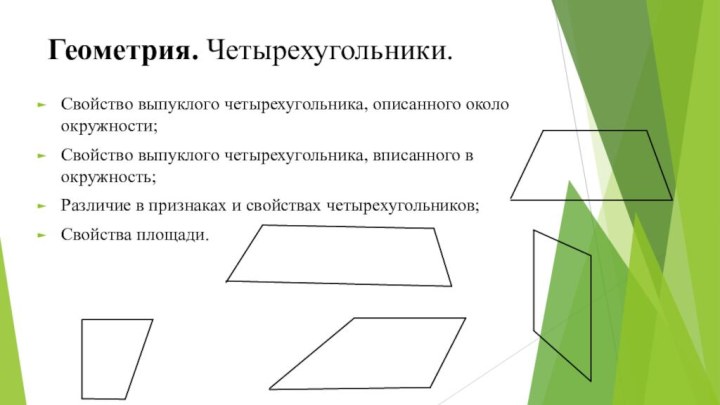
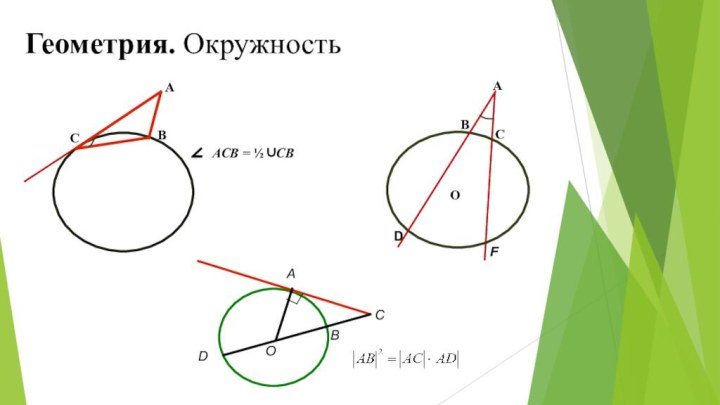
В прямоугольном треугольнике с прямым углом известны катеты:
. , . Найдите медиану этого треугольника.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам.
Найдите сторону АС, если сторона АВ равна 4.
Из вершины С прямого угла прямоугольного треугольника АВС проведём медиану СМ и высоту СН.