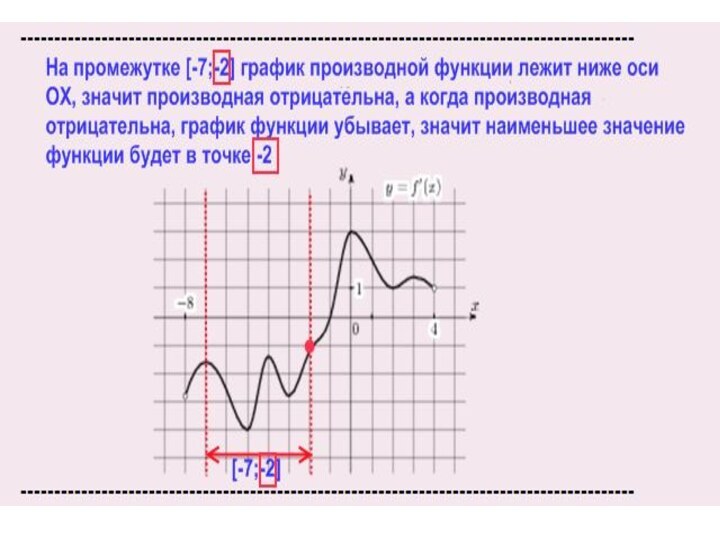
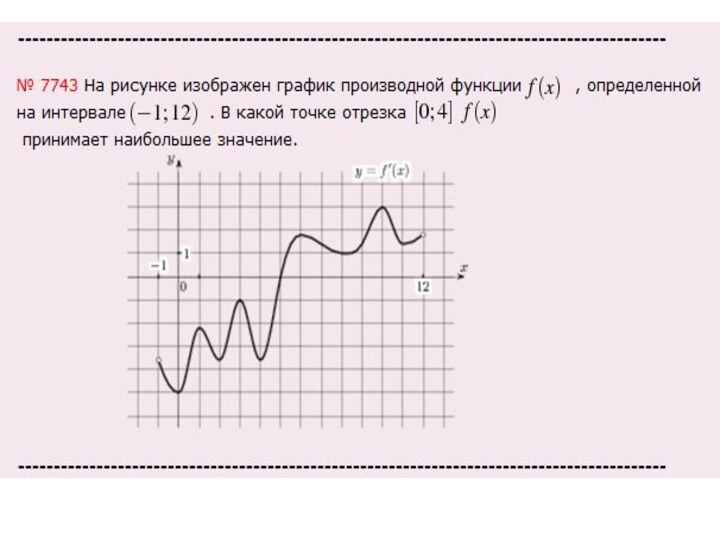
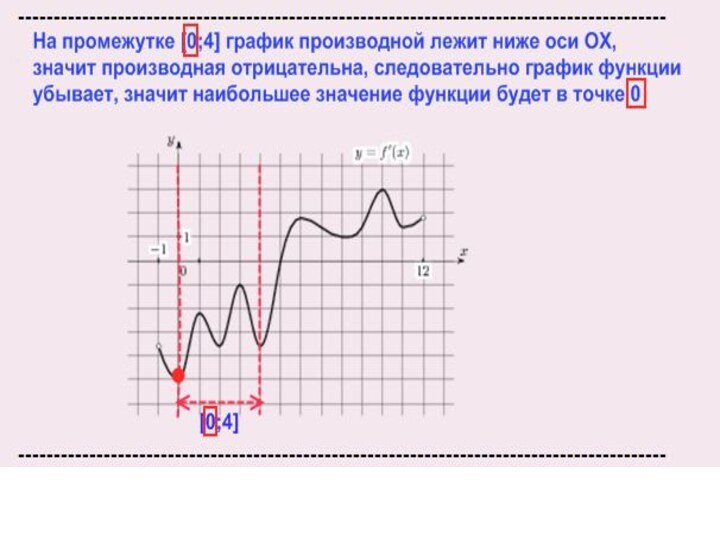
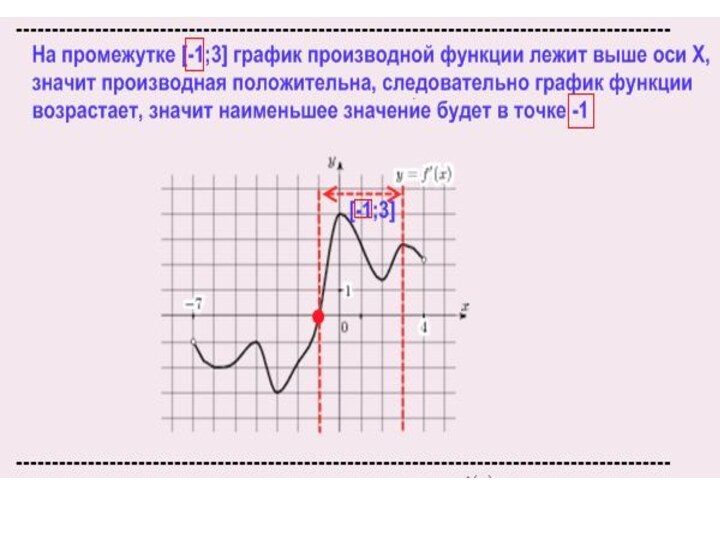
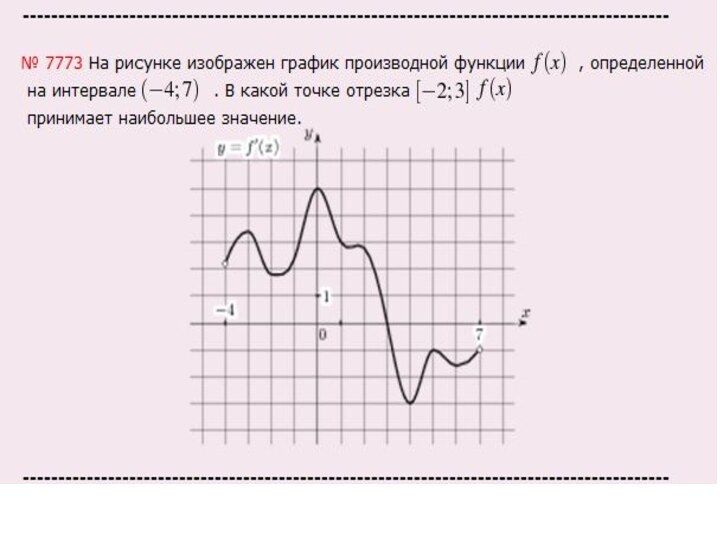
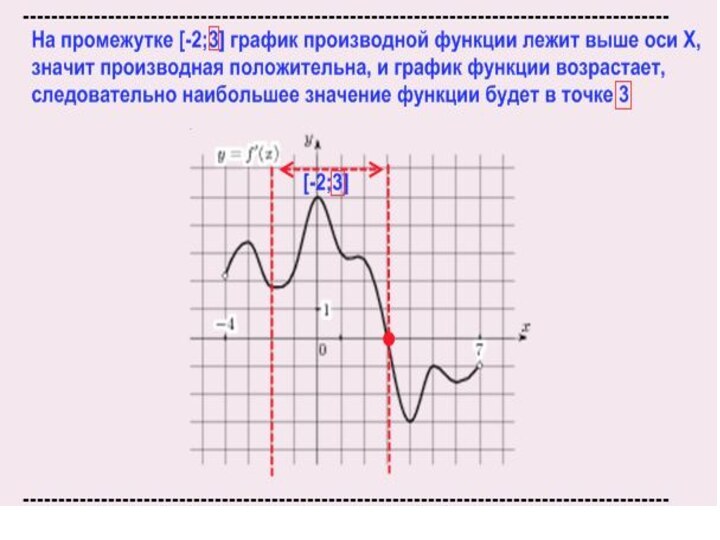
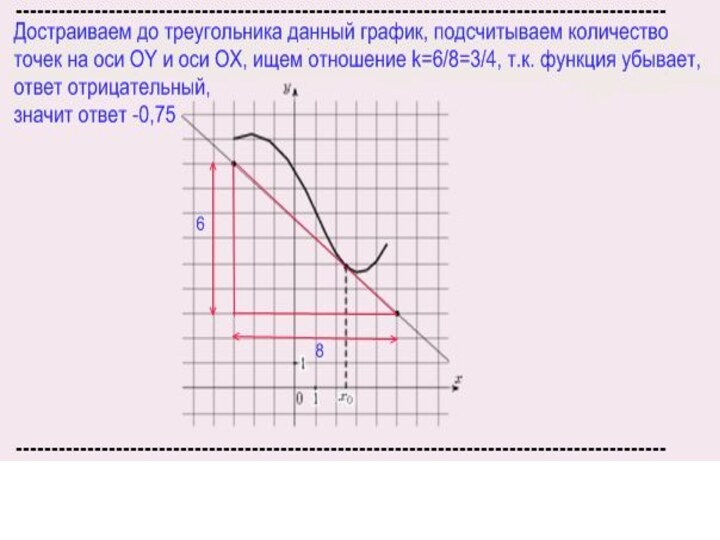
Слайд 3
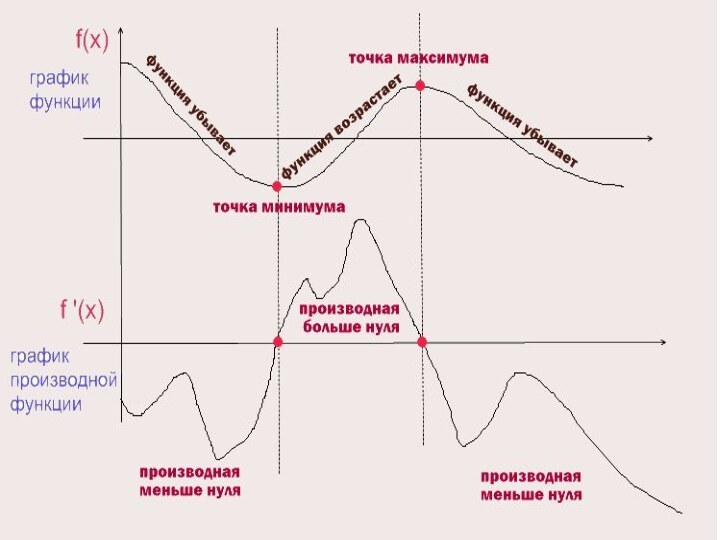
На схеме видно как ведет себя график функции
и график ее производной.
В момент когда график функции
убывает, график производной функции меньше нуля,
в момент когда график функции возрастает - производная больше нуля,
в момент когда график функции находится в своем минимуме или максимуме (эти точки называются экстремумы - красные точки на верхнем графике) - производная равна нулю (красные точки на нижнем графике).
Обратите внимание, что точка минимума графика функции соответствует точке в которой производная равна нулю, при условии, что график производной функции возрастает
и наоборот точка максимума графика функции соответствует точке в которой производная равна нулю, при условии, что график производной функции убывает.
Слайд 5
решение
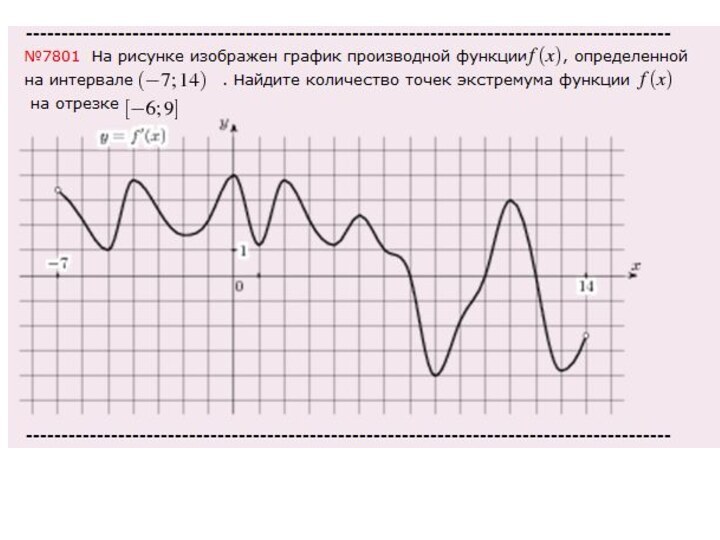
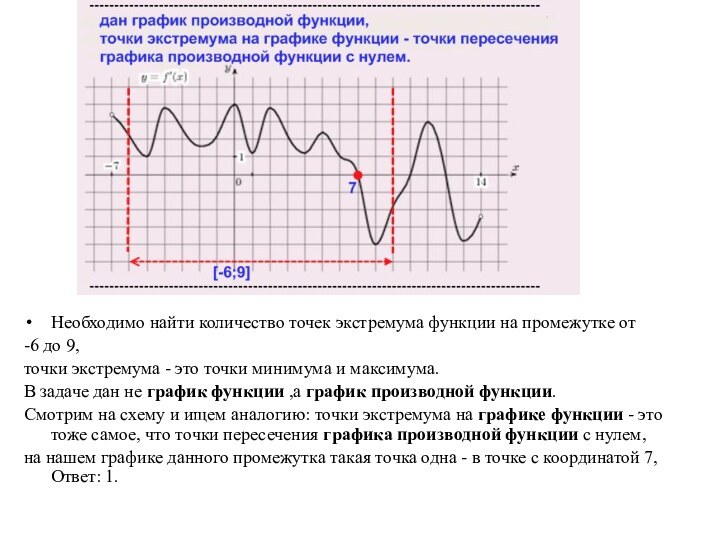
Необходимо найти количество точек экстремума функции на промежутке
от
-6 до 9,
точки экстремума - это точки
минимума и максимума.
В задаче дан не график функции ,а график производной функции.
Смотрим на схему и ищем аналогию: точки экстремума на графике функции - это тоже самое, что точки пересечения графика производной функции с нулем,
на нашем графике данного промежутка такая точка одна - в точке с координатой 7, Ответ: 1.
Слайд 6
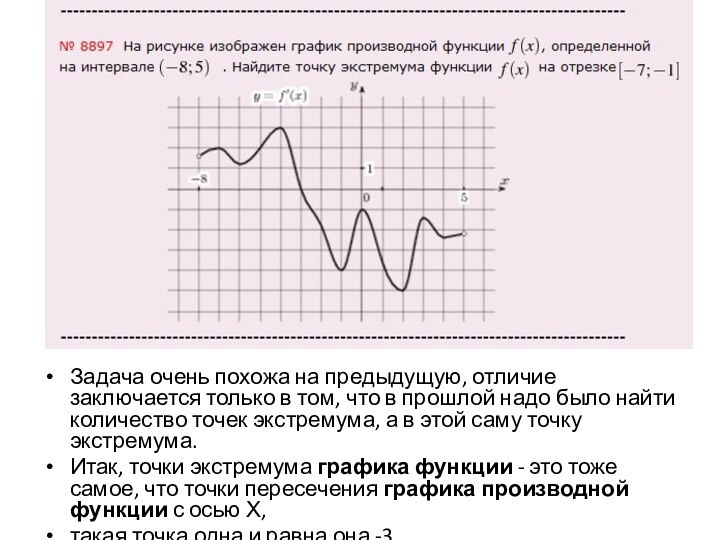
Задача очень похожа на предыдущую, отличие заключается только
в том, что в прошлой надо было найти количество
точек экстремума, а в этой саму точку экстремума.
Итак, точки экстремума графика функции - это тоже самое, что точки пересечения графика производной функции с осью Х,
такая точка одна и равна она -3.
Слайд 7
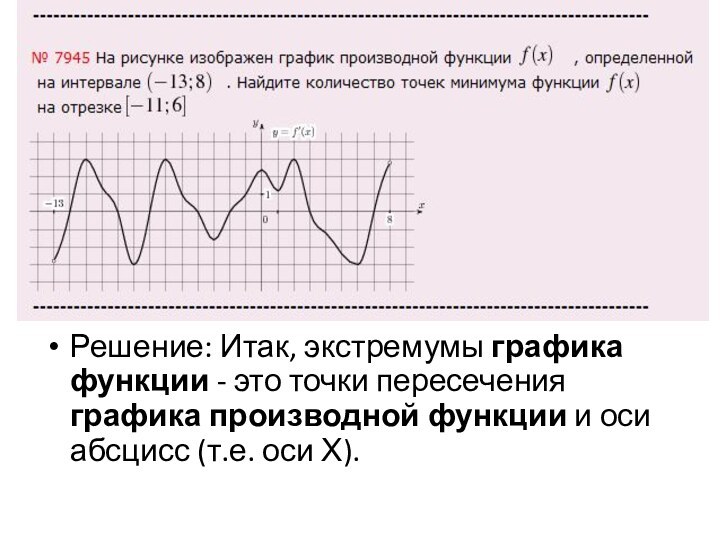
Решение: Итак, экстремумы графика функции - это точки
пересечения графика производной функции и оси абсцисс (т.е. оси
Х).
Слайд 8
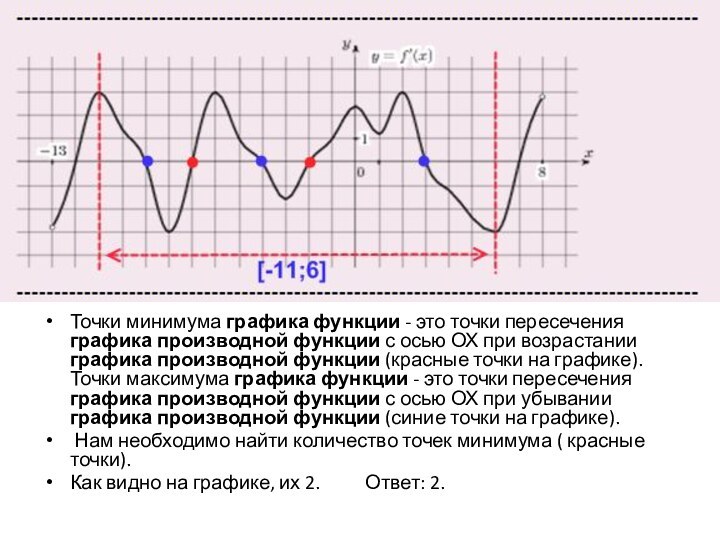
Точки минимума графика функции - это точки пересечения
графика производной функции с осью ОХ при возрастании графика
производной функции (красные точки на графике). Точки максимума графика функции - это точки пересечения графика производной функции с осью ОХ при убывании графика производной функции (синие точки на графике).
Нам необходимо найти количество точек минимума ( красные точки).
Как видно на графике, их 2. Ответ: 2.
Слайд 9
Нахождение наибольших и наименьших значений
графика функции на
заданном промежутке
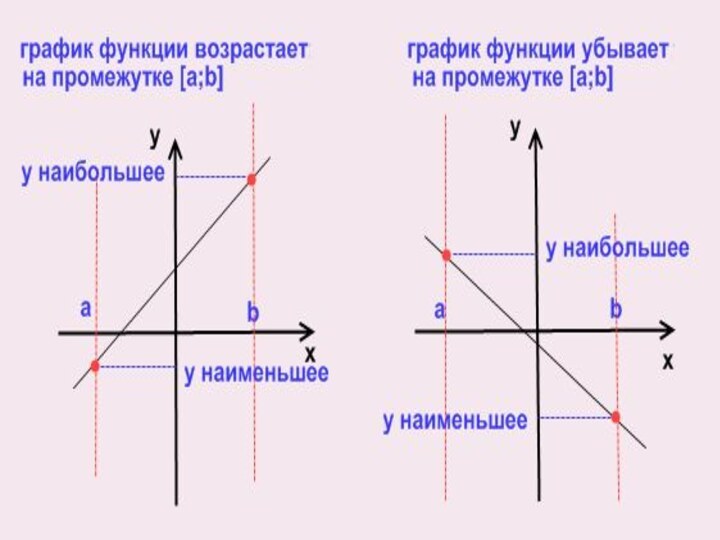
Если график функции возрастает, то первое значение отрезка
на котором надо найти наибольшее или наименьшее значение функции будет наименьшим, а второе – наибольшим
И наоборот, если график функции убывает, то первое значение отрезка на котором надо найти наибольшее или наименьшее значение функции будет наибольшим, а второе - наименьшим.
Слайд 19
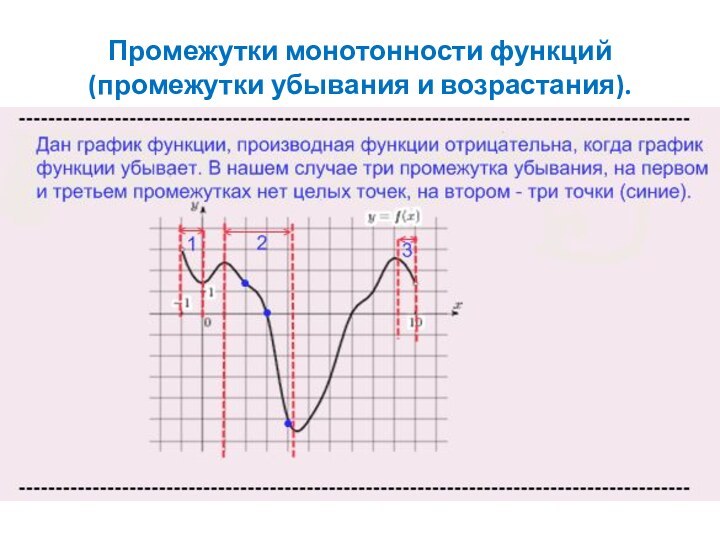
Промежутки монотонности функций
(промежутки убывания и возрастания).
Слайд 20
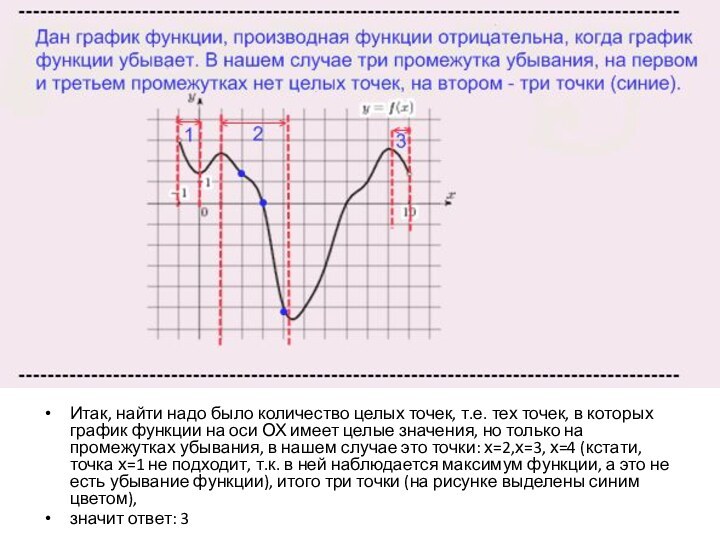
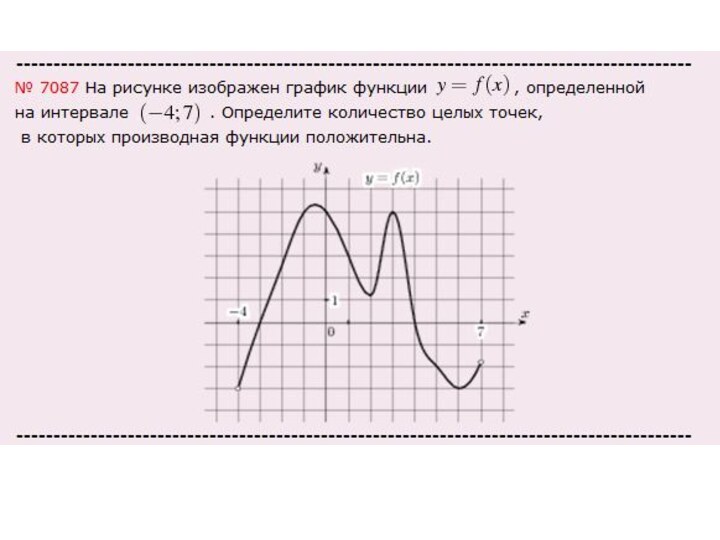
Итак, найти надо было количество целых точек, т.е.
тех точек, в которых график функции на оси ОХ
имеет целые значения, но только на промежутках убывания, в нашем случае это точки: х=2,х=3, х=4 (кстати, точка х=1 не подходит, т.к. в ней наблюдается максимум функции, а это не есть убывание функции), итого три точки (на рисунке выделены синим цветом),
значит ответ: 3
Слайд 22
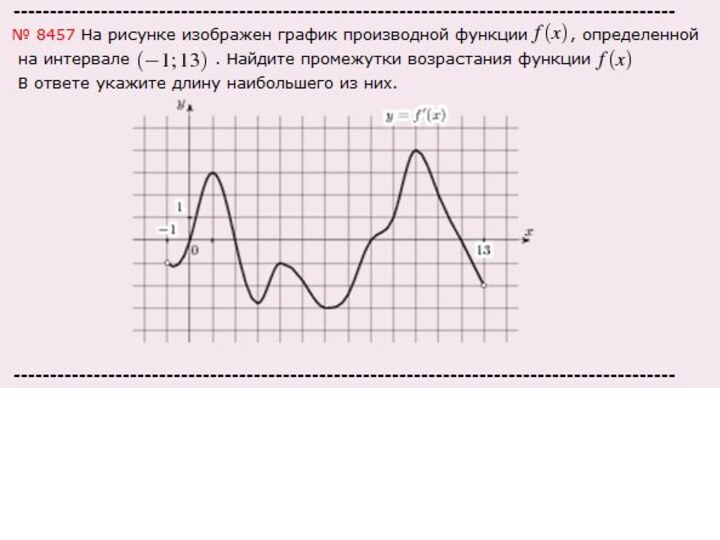
Итак, найти надо было количество целых точек, т.е.
тех точек, в которых график функции на оси ОХ
имеет целые значения, но только на промежутках возрастания, в нашем случае это точки: х=-3,х=-2, х=-1 (кстати, точка х=-4 (обведена красным) не подходит, т.к. она исключена),
итого три точки (на рисунке выделены синим цветом), значит ответ: 3.
Слайд 24
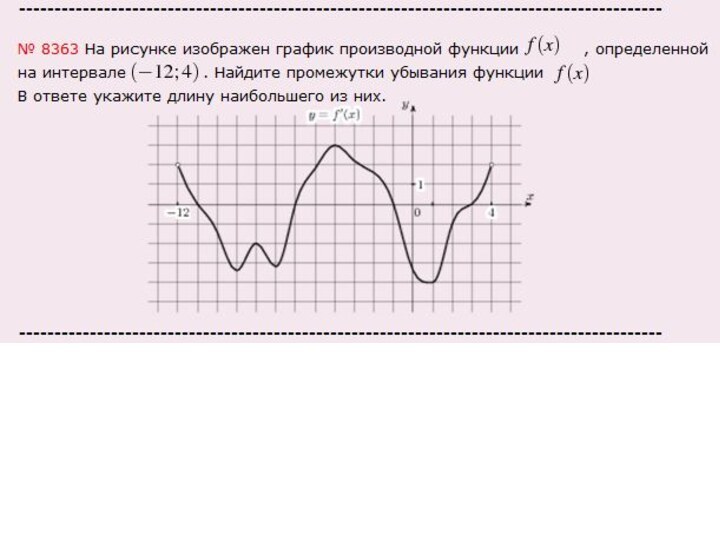
На графике видно, что наибольший промежуток - это
второй, его длина равна 4, значит ответ: 4
Слайд 26
На графике видно, что наибольший промежуток - это
первый, его длина равна 5,
значит ответ: 5.
Слайд 29
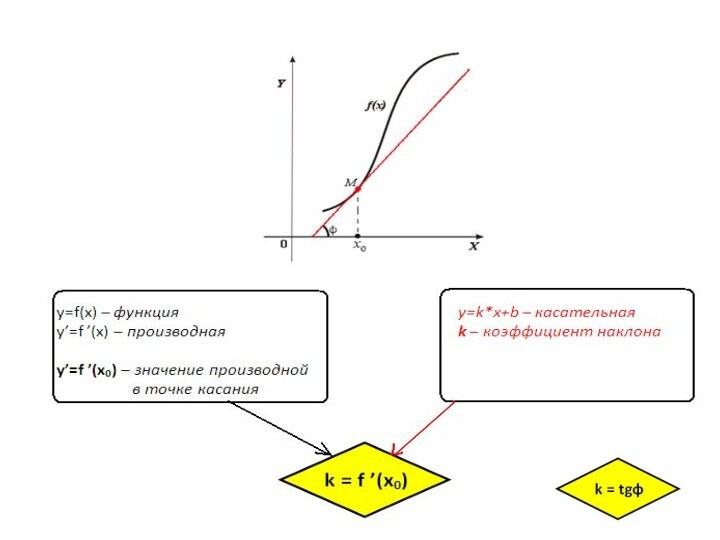
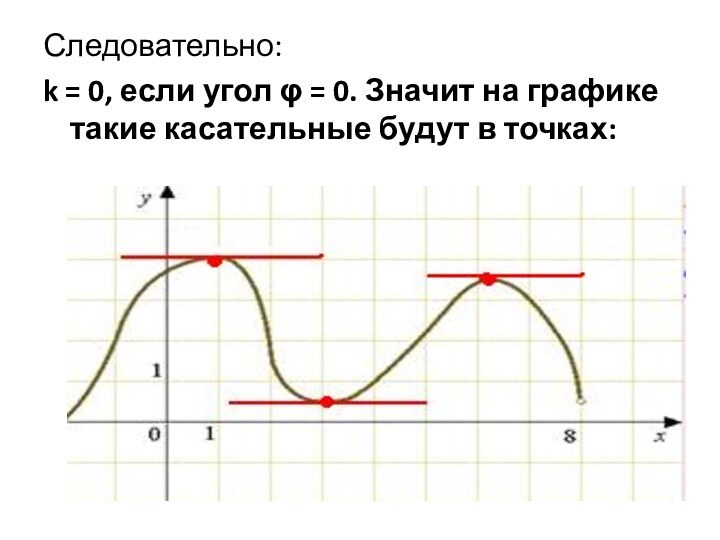
Следовательно:
k = 0, если угол φ = 0.
Значит на графике такие касательные будут в точках:
Слайд 30
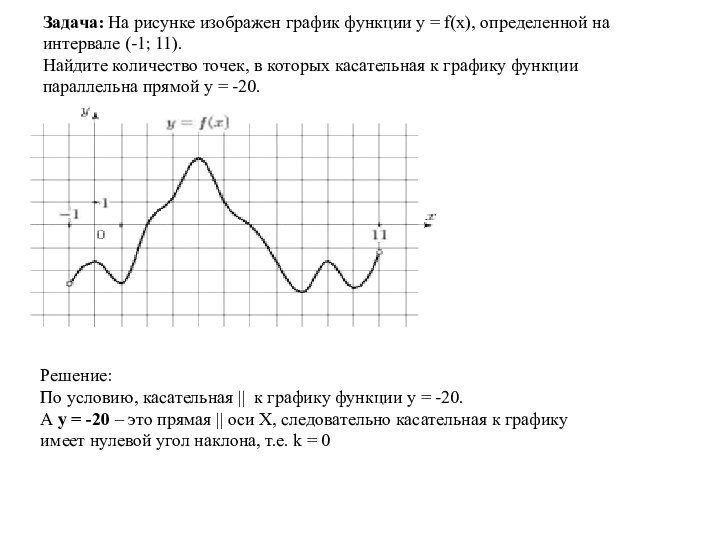
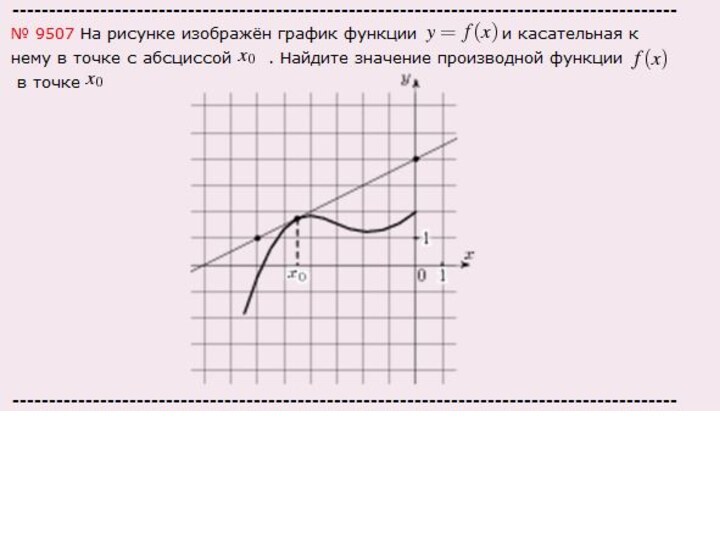
Задача: На рисунке изображен график функции y =
f(x), определенной на интервале (-1; 11).
Найдите количество точек,
в которых касательная к графику функции параллельна прямой y = -20.
Решение:
По условию, касательная || к графику функции y = -20.
А y = -20 – это прямая || оси Х, следовательно касательная к графику имеет нулевой угол наклона, т.е. k = 0
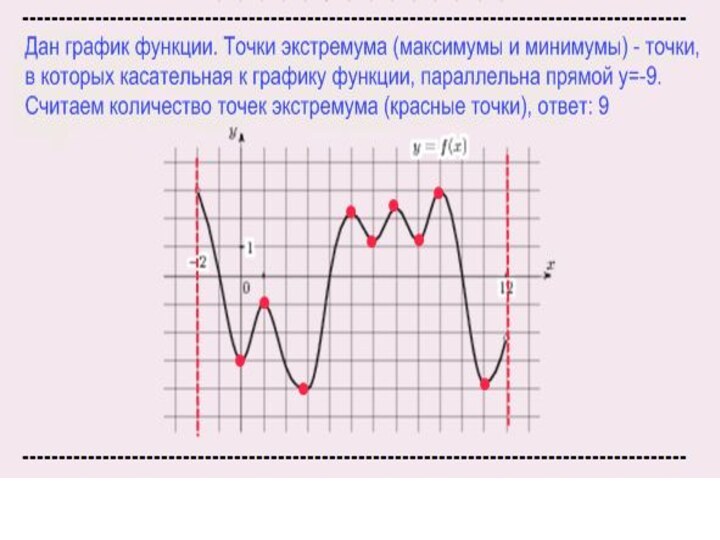
Слайд 33
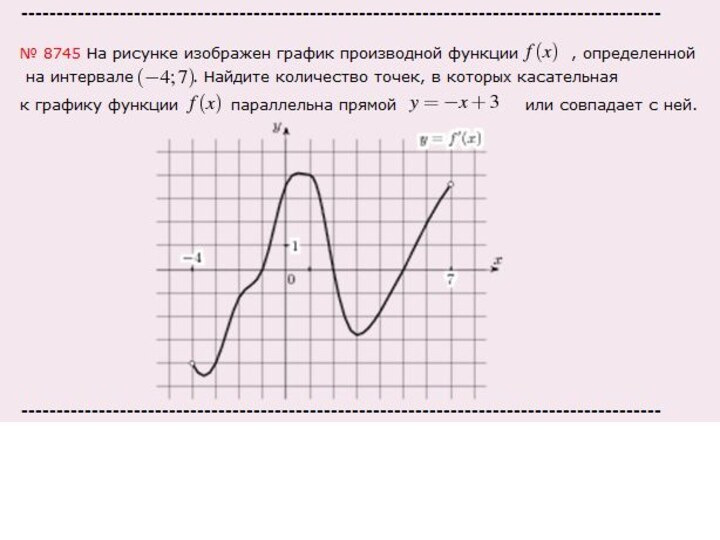
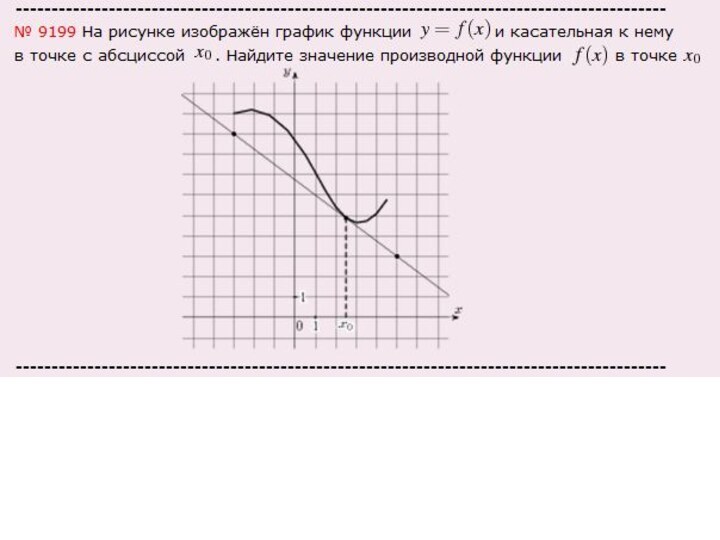
Во втором случае задан график производной функции, для
нахождения количества точек, в которых касательная к графику функции
параллельна, необходимо:
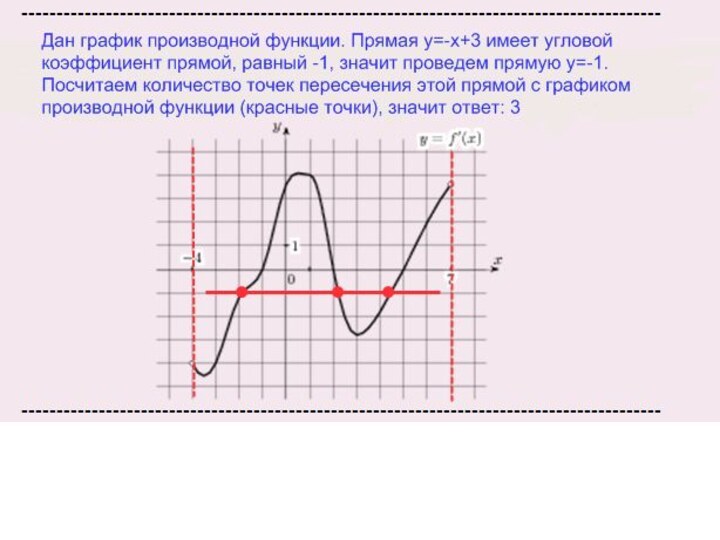
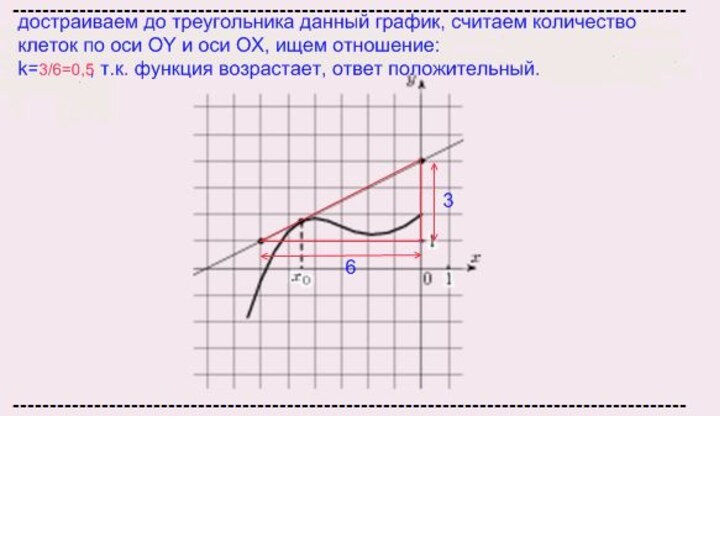
1. Найти угловой коэффициент касательной. Это можно сделать двумя способами:
Найти производную функции графика прямой, это и есть угловой коэффициент прямой;
Взять число, которое стоит перед Х в уравнении, например. если y=2х+5, то угловой коэффициент равен 2, если y=-х+3, то угловой коэффициент равен -1
2. провести прямую параллельно оси ОХ через точку на оси ОY, равную угловому коэффициенту прямой.
3. Подсчитать количество точек пересечения этой прямой с графиком производной функции.
Слайд 36
Угловой коэффициент касательной