- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Производная и её применение в алгебре,геометрии
Содержание
- 2. Цель работы:Закрепление изученного материала по теме «Производная» и ознакомление с её прикладной частью.
- 3. План работы:1. Определение производной.2.Исследование функции на монотонность.3.Касательная к графику.4.Правила вычисления производных.
- 4. Определение производной Производной данной функции
- 5. . Будем считать, что рассматриваемая функция y=f(x)
- 6. Решение: Чтобы применить признаки возрастания
- 9. 1.Найдите производные функций.1. f (x) = x^2
- 10. Скачать презентацию
- 11. Похожие презентации









Слайд 2
Цель работы:
Закрепление изученного материала по теме «Производная» и
ознакомление с её прикладной частью.
Слайд 3
План работы:
1. Определение производной.
2.Исследование функции
на монотонность.
3.Касательная к графику.
4.Правила вычисления производных.
Слайд 4
Определение производной
Производной данной функции в
точке х называется предел отношения приращения этой функции к
приращению аргумента в точке х, когда приращение аргумента стремится к нулю.
Слайд 5
.
Будем считать, что рассматриваемая функция y=f(x) определена
и дифференцируема в каждой точке отрезка a ≤ x
≤ b.функция f(x) возрастает (или убывает) в промежутке a
Пример. Определить промежутки возрастания и убывания функции: у = х3 — х2 — 8х + 2.
Слайд 6 Решение: Чтобы применить признаки возрастания и
убывания функции, найдем производную данной функции и определим значения
х, при которых она положительна или отрицательна:у' = Зх2 — 2х — 8.
Корни трехчлена: x1= - 4/3, x2=2.
Отсюда:
у' =3(х+4/3)(х-2).
возрастает убывает возрастает
+ -4/3 - 2 +
Ответ: функция возрастает в промежутках
- ∞ < x < -4/3 и 2 < x < + ∞ и убывает в промежутке — 4/3 < х <2.
Слайд 7
Вообразим, что на кривой АВ точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ.
Слайд 8
Правило 1: Если функции u и v дифференцируемы в точке х0, то и сумма дифференцируема в этой точке и
(u + v)’ = u’ + v’
Правило 2: Если функции u и v дифференцируемы в точке х0, то и произведение дифференцируемы этой точке и
(uv)’ = u’v + uv’
Правило 3: Если функции u и v дифференцируемы в точке х0 функция v не равна нулю в этой точке, то частное u/v также дифференцируемо в х0 и
(u/v)’ = u’v – uv’/v^2
Правила вычисления производных
Слайд 9
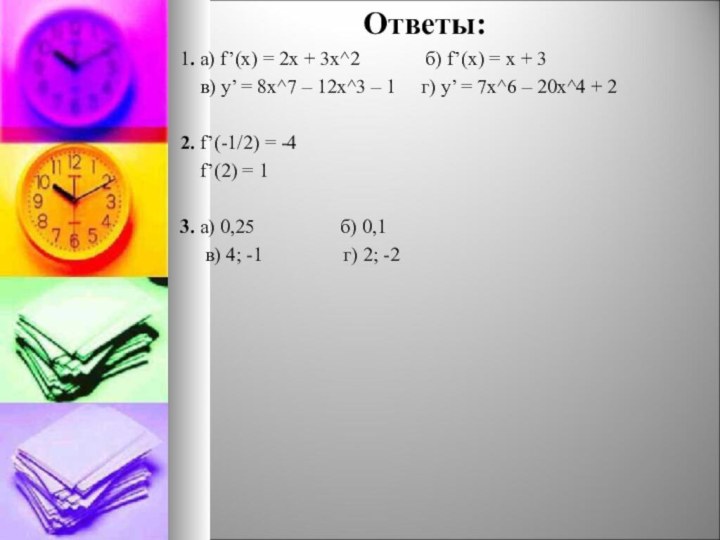
1.Найдите производные функций.
1. f (x) = x^2 +
x^3
2. f (x) = x^2 + 3x – 13. y = x^8 – 3x^4 – x + 5 4. y = x^7 – 4x^5 + 2x - 1
2.Вычислите значения производной функции f в данных точках:
f (x) = x^2 – 3x, если х = -1/2, х = 2
3.Решите уравнение f ‘(x) = 0, если:
а) f (x) = 2x^2 – x б) f (x) = -2/3x^3 + x^2 + 12
в) f (x) = x^3/3 – 1,5x^2 – 4x г) f (x) = 2x – 5x^2