- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Игровые и стратегические задачи
Содержание
- 2. Учитель математики МБОУ «Школа-лицей им. Героя Советского Союза Ф.Ф.Степанова» г.Саки Республика КрымЗагоря Т.М.
- 3. Известный русский математик В. П. Ермаков говорил:
- 5. Математические игры очень популярны, как, впрочем, и
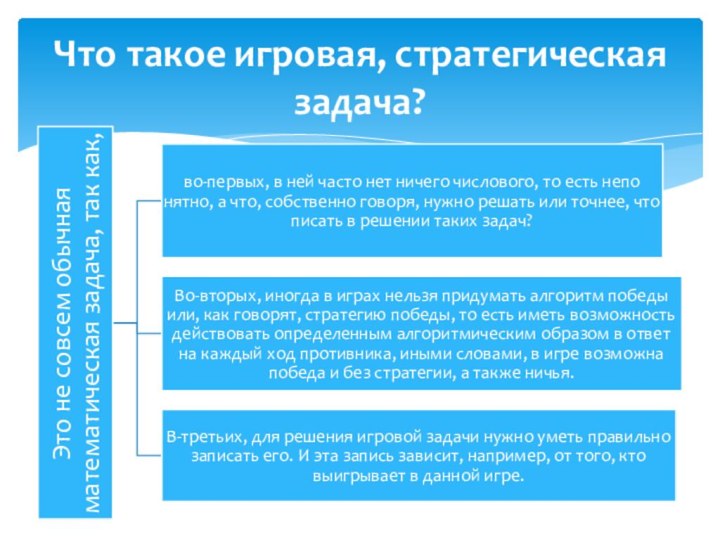
- 6. Что такое игровая, стратегическая задача?
- 7. Так как же правильно записать решение игровой задачи?
- 8. Цели работы:
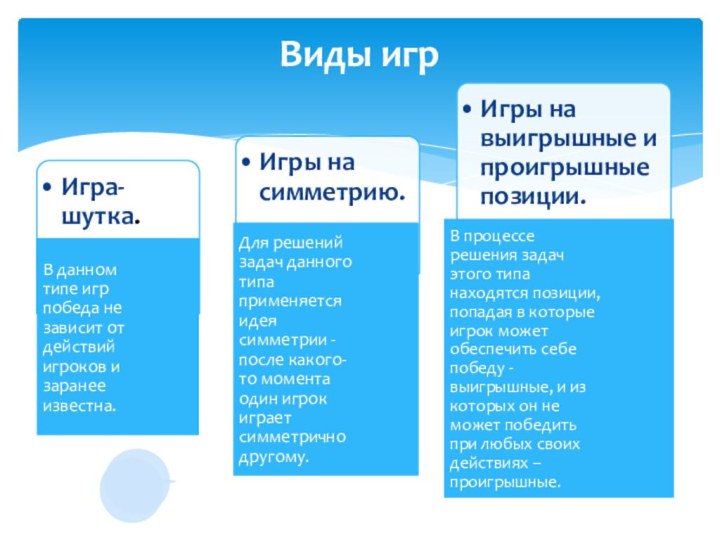
- 9. Виды игр
- 10. Игры – шутки – это такие
- 11. Задача. Двое по очереди ломают шоколадку 5x8.
- 12. Очень простой и красивый метод решения игровых
- 13. Задача 1. На окружности взято 20 точек.
- 14. Задача 2. Имеется две кучки камней —
- 15. Другая идея выигрышной стратегии в играх —
- 16. Задача. Двое играют в игру. Ходы, которые
- 17. 4. Метод выигрышных позиций. Этот метод основан
- 18. Задача.Имеются две кучки конфет: в одной —
- 19. Скачать презентацию
- 20. Похожие презентации
Учитель математики МБОУ «Школа-лицей им. Героя Советского Союза Ф.Ф.Степанова» г.Саки Республика КрымЗагоря Т.М.

















Слайд 3
Известный русский математик В. П. Ермаков говорил:
«В
математике следует помнить не формулы, а процесс мышления».Это демонстрируют задачи с играми.
Слайд 5 Математические игры очень популярны, как, впрочем, и все
игры. И далеко не всегда более сложная игра –
более интересная. В России даже существует Крупнейший русскоязычный форум о стратегических играх.Слайд 10 Игры – шутки – это такие игры,
где для построения выигрышного алгоритма можно ничего и не
знать, так как в них результат будет зависеть не от игры партнеров, а от начальных условий. Однако для этого в решении нужно заметить, что это игра-шутка, а не какая-то другая, в которой нужно искать выигрышную стратегию. На самом деле, нет никакой стратегии Просто... как бы кто ни ходил, либо всегда выиграет первый игрок (тот, кто начинает игру), либо всегда второй. Задача в том, чтобы математически доказать такую закономерность.Часто для нахождения идеи решения задачи можно использовать «метод маленьких чисел», т. е. начинать поиск решения с небольших чисел.
1. Игры-шутки.
Слайд 11 Задача. Двое по очереди ломают шоколадку 5x8. За
ход можно разломать любой кусок по прямой линии между
дольками. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?Решение: Долек всегда будет 5x8=40 штук, а шоколадка в начале была одна. Заметим, что на каждом ходу один кусок шоколадки всегда разламывается на 2, т.е. количество различных кусков шоколадки увеличивается на 1. В начале это кол-во было равно 1, а в конце, как мы заметили, 40. Значит, игра продолжалась ровно 39 ходов. Поэтому последний (39-й) ход был обязательно ходом первого (его ходы - первый, третий и все с нечетными номерами) - и первый выиграл. Вот такая получилась шутка - как ни ходи, первый всегда выигрывает.
Если число кусочков шоколадки четно, тогда побеждает первый, если число нечетно, тогда второй.
Часто для нахождения идеи решения задачи можно использовать «метод маленьких чисел», т. е. начинать поиск решения с небольших чисел.
Слайд 12 Очень простой и красивый метод решения игровых задач
- симметричная стратегия. Суть его - делать каждый раз
ход, симметричный ходу противника или дополняющий его до чего-либо. Доказательство правильности нашей стратегии будет пользоваться тем, что после каждого нашего хода позиция симметрична: раз так, то если противник сумел сделать свой ход, то и мы сможем сделать ход, симметричный ему.2.Симметрия.
Слайд 13 Задача 1. На окружности взято 20 точек. Можно
за один ход соединить две точки отрезком , который
не пересекает другие отрезки. Проигрывает тот, кто не может сделать ход. Кто выиграет?Первым ходом провести отрезок, соединяющий 2 точки, разделив количество точек пополам, а далее отвечать симметричным ходом на каждый ход соперника.
Слайд 14 Задача 2. Имеется две кучки камней — по
7 в каждой. За ход можно взять любое количество
камней, но только из одной кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет?Несложно понять, как действовать игроку, делающему второй ход, чтобы победить в данной игре: он должен делать точно такие же ходы, как и первый, но только убирать камни он должен из той кучки, которую не тронул последним ходом его противник.
То есть, у победителя всегда есть ход после хода противника.
Понятна и общая стратегия выигрывающего, когда в кучках произвольное число камней:
- если число камней в кучках равное, то необходимо уравнивать число камней в кучках после хода начинающего, выполняя симметричные ходы. Выигрывает второй игрок;
- если же число камней в кучках неравное, тогда начинающий своим ходом уравнивает число камней в кучках и далее действует так же как, как и в первом случае. Здесь побеждает игрок, делающий первый ход.
В данной игре симметрия несколько необычная — вроде бы и не симметрия вовсе, однако, равенство камней в кучках, и «одинаковые» ходы, проводимые игроками очень ее напоминают.
На самом деле, нередкое явление: в зависимости от исходных данных одна и та же стратегия приносит успех то первому, то второму игроку.
Слайд 15 Другая идея выигрышной стратегии в играх — дополнение
хода соперника до некоторого фиксированного числа, уменьшая каждым «совместным»
ходом (т. е. ход первого и второго игрока) общее число элементов на некоторое постоянное число, что сводит игру к игре с меньшим числом элементов, т. е. более простой. Понятно, что победа в данной стратегии зависит от общего количества данных по условию элементов.Рассмотрим пример такой стратегии на конкретной задаче
3. Дополнение до фиксированного числа.
Слайд 16 Задача. Двое играют в игру. Ходы, которые делаются
по очереди, заключаются в том, что из кучки в
45 камней убирается любое число камней от 1 до 5. Выигрывает тот, кто возьмет последний камень. Кто выиграет в данной игре?Решение:И опять выработку стратегии лучше начинать с небольшого числа камешков. Понятно, что если в нашей кучке меньше шести камней, тогда выиграет первый игрок: он первым своим ходом заберет все камни.
Если бы в нашей кучке было 6 камешков, тогда понятно, что второй выиграет, так как он забрал бы все оставшиеся камни после первого хода начинающего.
Если камней семь? Что делать тогда первому? Ему нужно забрать один камень и свести задачу к предыдущему случаю. Аналогично надо выработать стратегию игры и для 7, 8, 9,10,11 камней.
Когда камней 12, то понятно, что выиграет второй: как бы первый не ходил, он своим ходом может взять такое количество камней, чтобы осталось ровно 6. А в этом случае он выигрывает, как мы уже разобрали.
Итак, если число камней делится на 6, то выигрывает второй, если не делится, то первый.
В нашей задаче 45 камней. Поэтому выигрывает первый, беря из кучки три камня и оставляя 42 камня. Далее после его последующих ходов в кучке будет оставаться соответственно 36, 30, 24, 18, 12, 6, 0, таким образом,
последний камень забирает первый игрок.
Слайд 17
4. Метод выигрышных позиций.
Этот метод основан на рассмотрении
каждой позиции с точки зрения пользы для игрока, которому
предстоит ход. Начинаем рассматривать с конца – с последнего хода, затем предпоследний и т.д.Слайд 18 Задача.Имеются две кучки конфет: в одной — 20,
в другой — 21. За ход нужно съесть все
конфеты в одной из кучек, а вторую разделить на две необязательно равные кучки. Проигрывает тот, кто не может сделать ход. Кто выиграет?Решение: Если мы решили использовать метод выигрышных позиций, то нам нужно найти эти выигрышные позиции. Чтобы их найти, рассмотрим простейшие случаи.
Простейшая выигрышная позиция для того игрока, кто ее создал: это 1 и 1. Понятно, что в этом случае побеждает тот, кто ходит вторым, так как у первого игрока нет хода.
Очевидно, что позиция 2 и 1 выигрышная для первого и проигрышная для второго.
Если 3 и 1, тогда второй вновь с победой, как несложно убедиться простой проверкой, так как есть ровно два хода.
Когда в кучках 3 и 2, победа у первого (убираем 3, делим 2).
Если же 3 и 3, тогда победа вновь возвращается ко второму, что можно показать простым перебором и т. д.
Замечаем закономерность: если в каждой из кучек по нечетному числу конфет, тогда позиция выигрышная для второго.
Если же хотя бы в одной из кучек четное число конфет, то такая позиция выигрышная для первого.
Своим первым ходом он может съест кучку из 21 конфеты, а кучу с 20 конфетами разделить на две, в которых нечетное количество конфет в обеих кучках (например, 19 и 1). Заметим, что последняя позиция, когда две кучки, по одной конфете в каждой, выигрышная, т. е. последний ход сделает первый.