Слайд 2
Цели урока:
Дидактическая:
закрепить и повысить качество знаний учащихся путем
применения поиска наибольшего и наименьшего значений функций к решению
прикладных задач;
повысить интерес к знаниям;
активизировать и обострить восприятие учебного материала;
Развивающая
помочь учащимся увидеть связь математики с жизнью;
формировать практические умения и навыки;
развивать творческое мышление;
Воспитательная
воспитывать уверенность в себе и в своих силах;
воспитывать чувство ответственности, умение действовать организованно;
учить ребят четко и доступно излагать свои мысли;
Методическая
показать важную роль математики в овладении навыками практического характера;
проведение нетрадиционных форм урока;
Тип урока: закрепление учебного материала.
Форма урока: деловая игра.
Средства обучения: компьютер, интерактивная доска.
Слайд 3
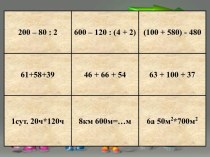
«Ярмарка» (устные упражнения)
Найти производные:
у = 2х – 3;
у = х2 – 2;
у = х2 –
3х + 4;
у = 3х2 – 6х;
у = 3х4 – 7х3 + 2х2 + π;
;
у = х-3 + 2x;
y = 2 sin x;
y = sin 2x;
y = cos 5x;
y = cos x;
Слайд 4
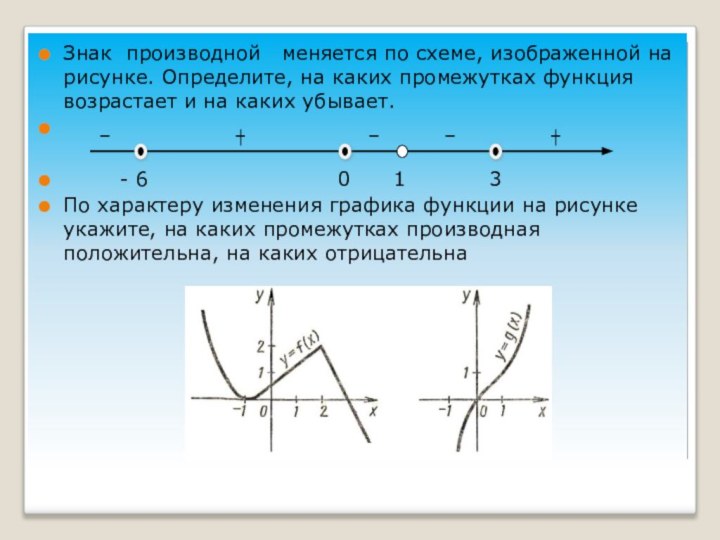
Знак производной меняется по схеме, изображенной на
рисунке. Определите, на каких промежутках функция возрастает и на
каких убывает.
- 6 0 1 3
По характеру изменения графика функции на рисунке укажите, на каких промежутках производная положительна, на каких отрицательна
Слайд 5
На рисунке изображены графики функций f(x) и g(x),
заданных на отрезке [a;b]. Для каждой из них найдите:
Точки
максимума и минимума
Точки, в которых функция принимает наибольшее и наименьшее значения на [a;b].
Слайд 6
Конкурс «главных инженеров»
(Проверка пройденного материала, 20 мин)
Каждый инженер
выбирает карточку – задание: найти наибольшее и наименьшее значения
функции (выполняют за столом, отдел помогает своему главному инженеру)
Кто первый готов, на доске показывает свое решение и так по очереди в порядке готовности;
Слайд 7
1. «Автостоянка»
Для стоянки машин выделили площадку прямоугольной формы,
которую надо обнести металлическим забором длиной 200м.
Какими должны
быть размеры площадки, чтобы ее площадь была наибольшей?
Слайд 8
Решение
Переведем задачу на математический язык – составим математическую
модель.
Длина забора – это периметр, прямоугольника, Р = 200м.
Пусть AD = x, DC = a, тогда PABCD = (х+а)*2 = 200, х+а=100, а=100 – х, где 0SABCD = x * a = x * (100 – x) = 100x – x2, 0Наша задача, исследовать функцию S(x) = 100x – x2, т.е. найти ее наибольшее значение на отрезке [0;100].
Вспоминаем алгоритм.
S’(x) = (100x – x2)’ = 100 – 2x
100 – 2x = 0 → 2x = 100 → x = 50 стационарная точка Ищем значение функции на концах отрезка и в стационарной точке;
S(0) = 100 * 0 – 02 = 0 S(50) = 100 * 50 – 502 = 2500 S(100) = 100 * 100 – 1002 = 0
Sнаиб = S(50) = 2500
Математические результаты переводим на реальную задачу:
Sнаиб = 2500м2, одна сторона х = 50м (это ранее найденная стац. точка), тогда вторая сторона а = 2500/50 = 50м, т.е. участок должен быть квадратной формы, чтобы площадь его была наибольшей.
Слайд 9
2. «Дача»
Старый плотник при изготовлении балки из цилиндрического
бревна поступает так:
Проводит на торце бревна диаметр АС;
Делит его
на 3 равные части точками К и L;
Проводит перпендикуляры LB и KD;
Принимает четырехугольник ABCD за сечение балки и стесывает лишнее (заштрихованное).
Наблюдавший за дедом внук задумался: «Почему дед делает балку именно так?»
Действительно, почему?
Слайд 10
Вопрос 1. Почему дед стесывает края?
Вопрос 2.
А какая прямоугольная балка, сделанная из этого бревна, будет
самой прочной?
Вопрос 3. А у деда получается эта, самая прочная балка?
Вопрос 4. А намного ли самая прочная балка прочнее бревна? Может стесывать вообще не надо?
Слайд 11
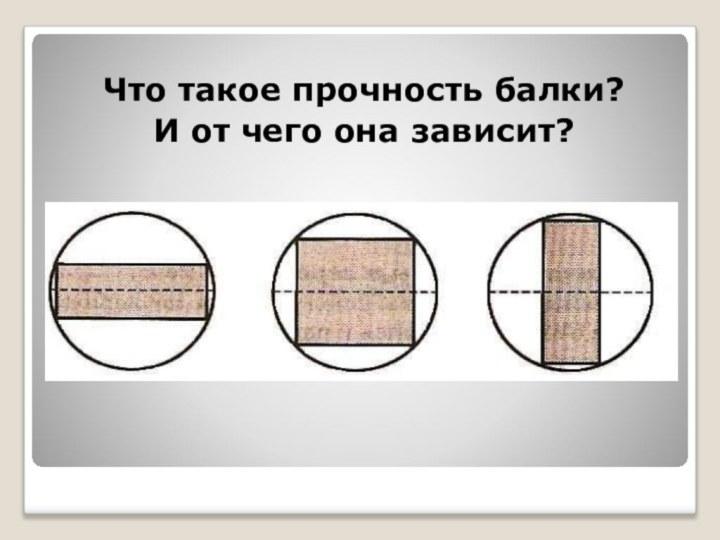
Что такое прочность балки?
И от чего она зависит?
Слайд 12
Прочность балки рассчитывается по формуле
F=kah²
где k – коэффициент
прочности, зависящий от материала, из которого изготовлена балка.
Значит
перед нами стоит задача:
каковы размеры прямоугольной балки наибольшей прочности, которую можно изготовить из цилиндрического бревна радиуса R?
Слайд 13
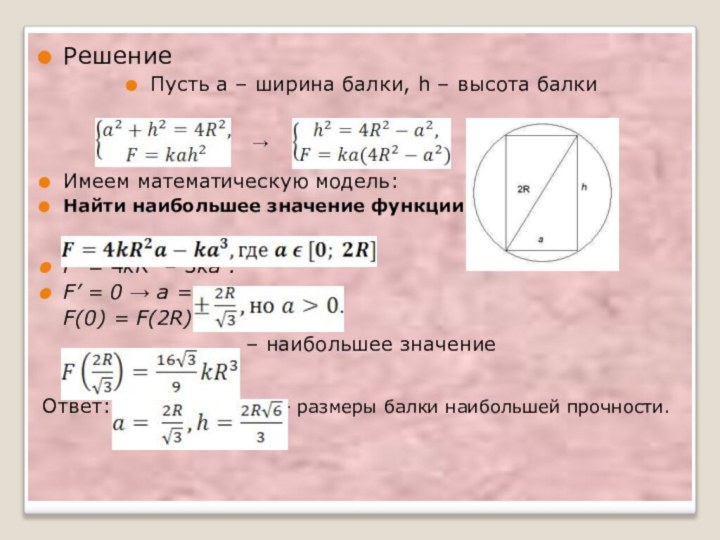
Решение
Пусть a – ширина балки, h – высота
балки
Имеем математическую модель:
Найти наибольшее значение функции
F’ = 4kR2
– 3ka3.
F’ = 0 → a =
F(0) = F(2R) = 0,
– наибольшее значение
Ответ: – размеры балки наибольшей прочности.
→
Слайд 14
3. Домашнее задание
Каковы должны быть размеры (радиус основания
R и высота H) открытой сверху цистерны максимальной вместимостью,
если для ее изготовления отпущено материала площадью S = 27π ≈ ≈ 85м2?



![Наибольшее и наименьшее значения функции На рисунке изображены графики функций f(x) и g(x), заданных на отрезке [a;b].](/img/tmb/6/543416/8a33ae10215d053cfe32b9c5a1683421-720x.jpg)