Слайд 2
Главная цель изучения математики
Изучение математики в школе
направлено
на достижение следующих целей:
овладение системой математических знаний и
умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Слайд 3
Головоломка «Пентамино»
«Пентамино» – это распространённая во всём
мире дидактическая игра - головоломка, в которую входит комплект
из двенадцати различных фигур, каждая из которых состоит из пяти одинаковых квадратов, соединенных между собой сторонами.
Правила игры очень простые: нужно, используя весь комплект фигур, полностью покрыть заданную фигуру, имеющую площадь 60 клеток.
Слайд 4
Как изготовить комплект фигур пентамино?
Слайд 5
Во-первых, для решения этих задач не требуется специальных
математических знаний, а их условия понятны школьникам любого класса.
Во-вторых, их решение требует значительных затрат времени, так как приходится рассматривать различные варианты и стратегии их решения.
Особенности задач пентамино
Эти задачи обладают всеми необходимыми свойствами, которые позволяют использовать их для организации различных интеллектуальных соревнований школьников:
Слайд 6
Наиболее интересными и сложными задачами пентамино считаются комплексные
задачи.
Мы их назвали комплексными, потому что такие задачи
содержат набор отдельных задач, объединенных общим условием.
Каждая из таких задач является самостоятельным исследованием, и её решение требует довольно значительных усилий и времени.
Комплексные задачи пентамино
Слайд 7
Примеры комплексных задач
Собрать 12 прямоугольников размерами 5 х
11, каждый без одного пентамино.
Слайд 8
Собрать 12 фигур в виде «рекламных щитов», состоящих
из 65 клеток, каждый с отверстием в виде одного
из пентамино.
Примеры комплексных задач
Слайд 9
Разработка и решение комплексных задач пентамино
Мною разработано более
тридцати комплексных задач пентамино.
Своим задачам я дала названия
по форме той фигуры, на которую они мне кажутся похожими, например: «змейки», «башни», «свечи» и т.д.
В серии задач «змейки» нужно собирать
все возможные фигуры,
которые можно получить при
однократных или двукратных
перегибах прямоугольника
3 × 20.
Слайд 16
Задачи «башни»
В задачах «башни – 1 и 2»
нужно
собрать 12 фигур в виде «башен», состоящих из 65
клеток, каждая с отверстием в виде одного из пентамино.
Слайд 18
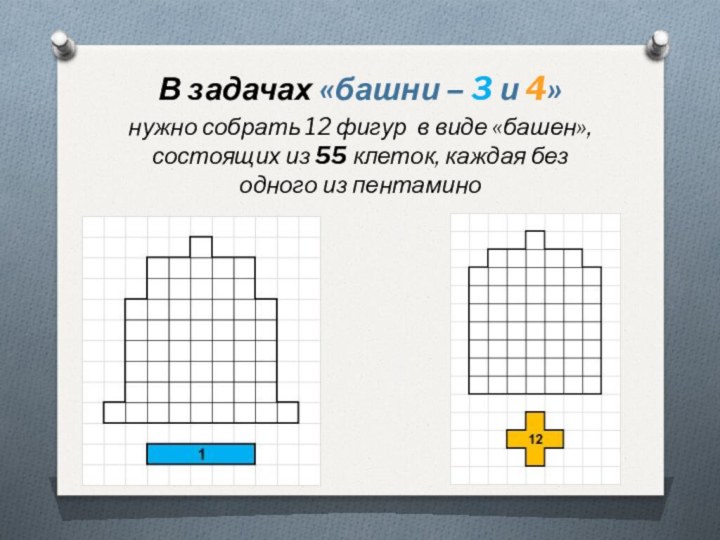
В задачах «башни – 3 и 4»
нужно собрать
12 фигур в виде «башен», состоящих из 55 клеток,
каждая без одного из пентамино
Слайд 20
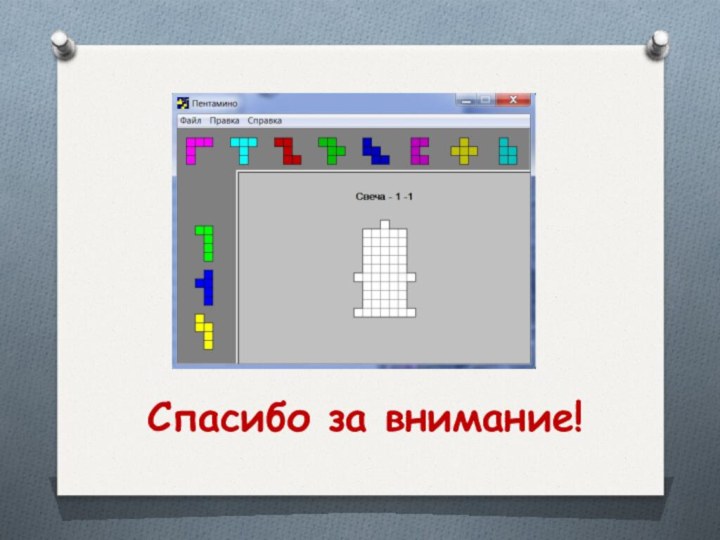
Задачи «свечи – 1, 2, … ,24, 25»
В
каждой из 25 задач «свечи»
нужно собрать 12 фигур в
виде «свечей», состоящих из 55 клеток, каждая без одного из пентамино.
Слайд 21
Анализ и классификация комплексных задач пентамино
В результате анализа
комплексных задач нам удалось составить их классификацию. Это позволяет
упорядочить придуманные задачи и упрощает разработку новых задач.
Мы разделили все комплексные задачи на три класса:
1. Задачи, в которых нужно собрать 12 фигур заданной формы, площадью 55 клеток, каждую без одной фигуры пентамино.
2. Задачи, в которых нужно собрать 12 фигур заданной формы, площадью 65 клеток, каждую с отверстием в виде одной из фигур пентамино.
3. Задачи, в которых нужно собрать полный комплект фигур площадью 60 клеток, форма которых меняется по заданному правилу.
К 1 классу относятся задачи: «свечи», «башни – 3 и 4» и другие.
Ко 2 классу относятся задачи С. Голомба, «башни – 1 и 2» и другие.
К 3 классу относятся задачи типа «змейки», задача Р. Робинсона и Дж. Таккера (только в ней фигуры имеют площадь не 60, а 45 клеток).
Слайд 22
Проведение интеллектуальных соревнований в некоторых классах гимназии №
44 г. Иркутска по решению комплексных задач пентамино.
Слайд 23
Как оценивать задачи?
1. Задачи первого класса (в которых
нужно собрать 12 фигур заданной формы, площадью 55 клеток,
каждую без одной фигуры пентамино).
За первую собранную фигуру – 1 балл, а за каждую следующую – на один балл больше.
За всю серию – 78 баллов.
2. Задачи второго класса (в которых нужно собрать 12 фигур заданной формы, площадью 65 клеток, каждую с отверстием в виде одной из фигур пентамино).
За первую собранную фигуру – 2 балла, а за каждую следующую – на один балл больше.
За всю серию – 90 баллов.