Презентация на тему Графическое решение квадратных уравнений

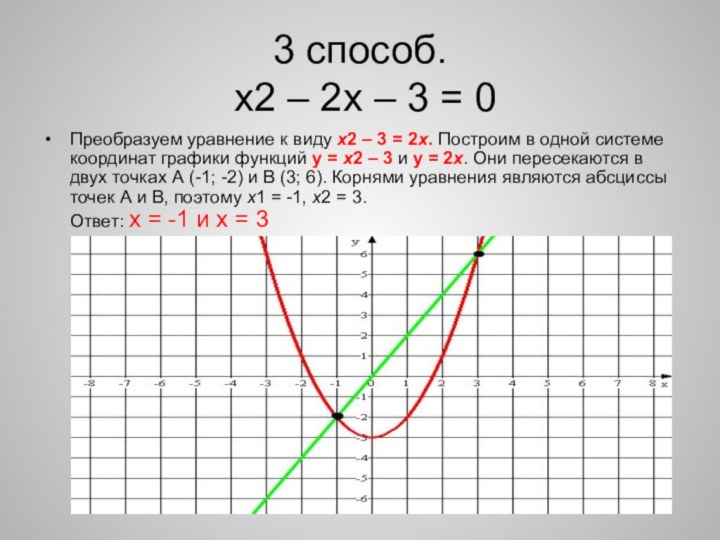
график функции y = x2 – 2x – 3

1)Имеем: a = 1, b = -2,
x0 = -b ÷ 2a = 1,
y0 = f(1) = 12 – 2 – 3 = -4.
Значит, вершиной параболы служит точка (1; -4),
а осью параболы – прямая x = = 1.
2) Возьмём на оси x две точки, симметричные относительно оси параболы, например точки x = -1 и x = 3.
3) Имеем f(-1) = f(3) = 0. Построим на координатной плоскости точки (-1; 0) и (3; 0).
4) Через точки (-1; 0), (1; -4), (3; 0) проводим параболы.
Построим прямую y=0
Корнями уравнения x2 – 2x – 3 = 0 являются абсциссы точек пересечения параболы с осью х; значит, корни уравнения таковы x1 = -1 и x2 = 3
Ответ: х = -1 и х = 3

0
Преобразуем уравнение к виду x2 = 2x + 3.

Построим в одной системе координат графики функций y = x2 и y = 2x + 3. Они пересекаются в двух точках А (-1; 1) и В (3; 9). Корнями уравнения служат абсциссы точек А и В, значит, х1 = -1, х2 = 3. Ответ: х = -1 и х = 3

0
Преобразуем уравнение к виду х2 – 3 = 2х.

Построим в одной системе координат графики функций у = х2 – 3 и у = 2х. Они пересекаются в двух точках А (-1; -2) и В (3; 6). Корнями уравнения являются абсциссы точек А и В, поэтому х1 = -1, х2 = 3. Ответ: х = -1 и х = 3

0
Преобразуем уравнение к виду
х2 – 2х +1 –

4 = 0 и далее х2 – 2х + 1 = 4, т.е. (х – 1)2 = 4 Построим в одной системе координат параболу у = (х – 1)2 и у = 4. Они пересекаются в двух точках А (-1; 4) и В (3; 4). Корнями уравнения служат абсциссы точек А и В, х1 = -1, х2 = 3. Ответ: х = -1, х = 3

0
Разделив почленно обе части уравнения на

х, получим
х – 2 – 3 / х = 0.
И далее х – 2 = 3/х. Построим в одной системе координат гиперболу у = 3 / х и
у = х – 2. Они пересекаются в двух точках А (-1; -3) и В (3; 1). Корнями уравнения являются абсциссы точек А и В, следовательно, х1 = -1,
х2 = 3. Ответ: х = -1, х = 3

= 0 мы решили графически пятью способами. Давайте проанализируем,

в чем суть этих способов