Слайд 2
Цель исследования:
знакомство учащихся с легкими
способами запоминания
таблицы
умножения.
Гипотеза исследования:
существуют различные способы,
которые помогают запомнить та-
блицу
умножения, а также законо-
мерности в строении самой табли-
цы умножения.
Слайд 3
Задачи исследования:
- выявить закономерности и интерес-ные свойства
таблицы умножения;
поиск других способов заучивания таблицы умножения;
Методы исследования:
поисковый метод;
исследовательский
метод;
практический метод;
Слайд 6
Умножение на 1 и 10
«При умножении числа на
единицу получается то же число»
а • 1 = а
«При
умножении числа на 10,
нужно справа дописать к этому
числу 0»
Слайд 7
Исключаем случаи
умножения на 1 и 10
Слайд 8
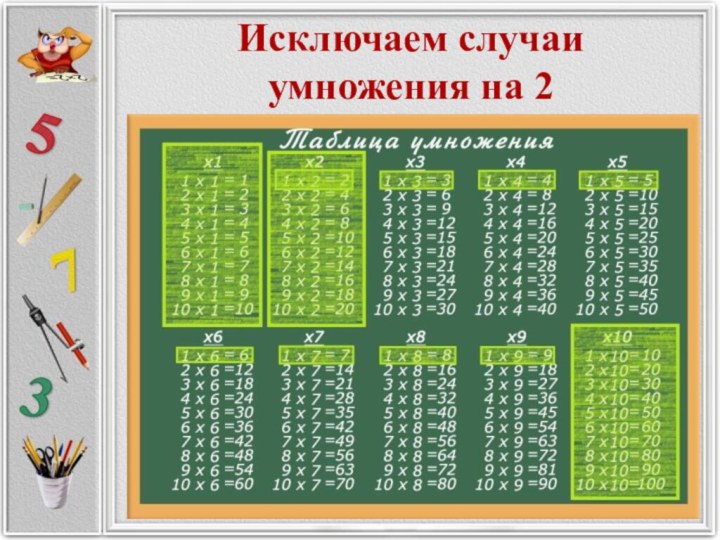
Исключаем случаи
умножения на 2
Слайд 9
Коммутативный (переместительный) закон
« Результат сложения (умнож.) не зависит
от порядка слагаемых (множителей) »
a + b = b
+ a
a • b = b • a
Слайд 12
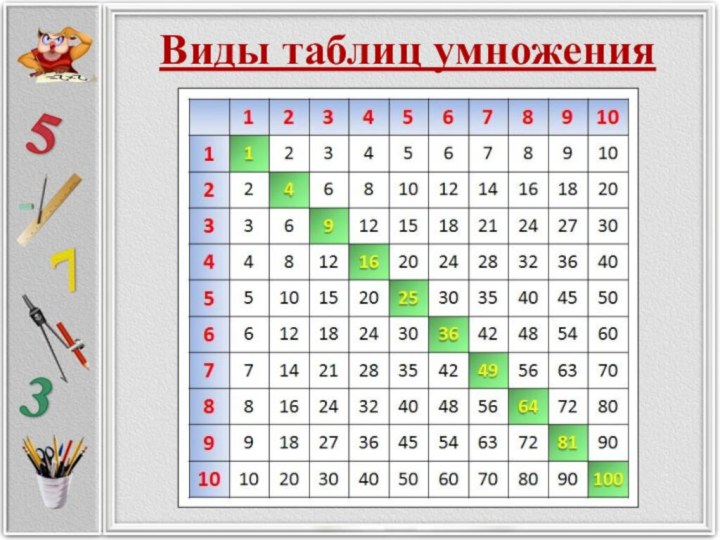
Закономерности таблицы Пифагора
Слайд 13
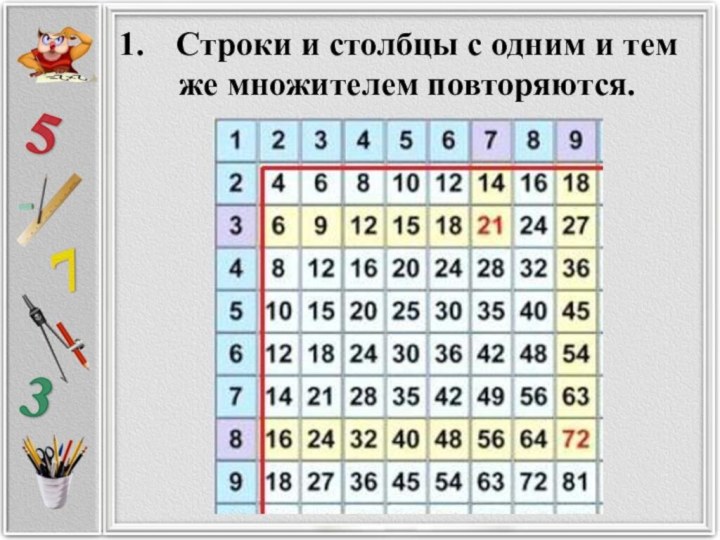
Строки и столбцы с одним и тем
же множителем повторяются.
Слайд 14
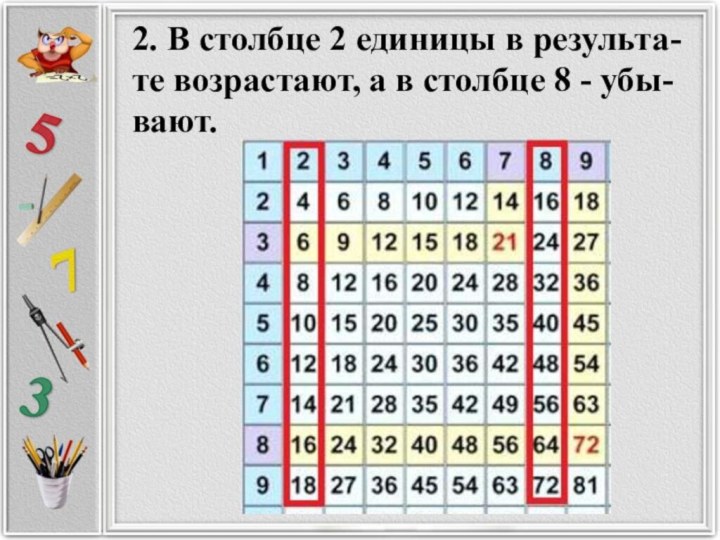
2. В столбце 2 единицы в результа-
те возрастают,
а в столбце 8 - убы-
вают.
Слайд 15
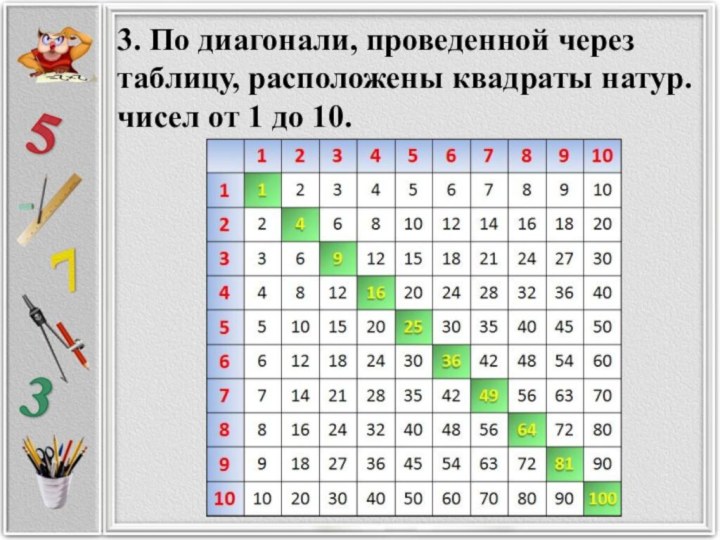
3. По диагонали, проведенной через таблицу, расположены квадраты
натур. чисел от 1 до 10.
Слайд 16
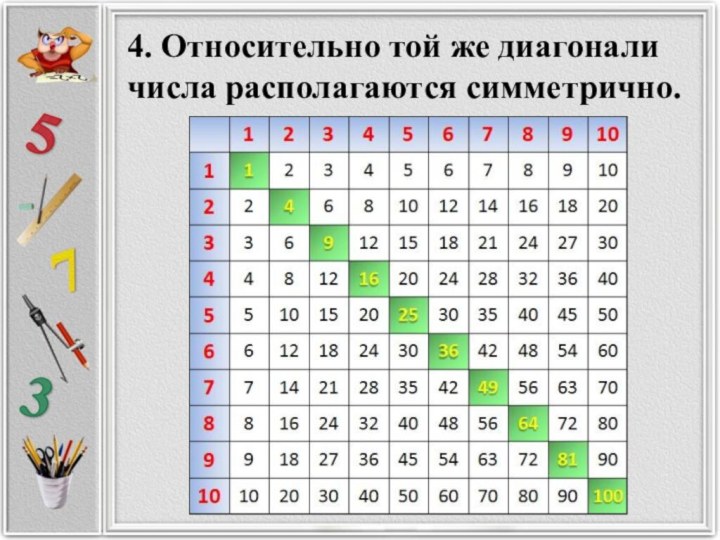
4. Относительно той же диагонали числа располагаются симметрично.
Слайд 17
5. Суммы чисел, расположенных
на одинаковом расстоянии от
5-го
столбика, всегда равны и в два раза
больше числа,
записанного в центре.
1 + 9 = 10;
10 = 2 х 5;
2 + 18 = 20;
20 = 2 х 10;
3 + 27 = 30;
30 = 2 х 15;
Слайд 18
6. При умножении чисел от 1 до 10
на
2 цифры 0, 2, 4, 6, 8 повторяются
в
разделе единиц.
1 х 2 = 2; 6 х 2 = 12;
2 х 2 = 4; 7 х 2 = 14;
3 х 2 = 6; 8 х 2 = 16;
4 х 2 = 8; 9 х 2 = 18;
5 х 2 = 10; 10 х 2 = 20;
Слайд 19
7. При умножении на 3 в ответах
появляется следующая закономер-
ность:
сначала идут числа 3, 6, 9;
затем
три двузначных числа, у которых первая цифра 1, но сумма цифр равна 3, 6 и 9;
затем идут три двузначных числа, у которых первая цифра 2, а сумма цифр остается в таком же порядке: 3, 6, 9;
Слайд 20
1 х 3 = 3
2 х 3 =
6
3 х 3 = 9
4 х 3 = 12
5
х 3 = 15
6 х 3 = 18
7 х 3 = 21
8 х 3 = 24
9 х 3 = 27
3, 6, 9 (п.1)
1 + 2 = 3,
1 + 5 = 6,
1 + 8 = 9,
2 + 1 = 3,
2 + 4 = 6,
2 + 7 = 9,
Слайд 21
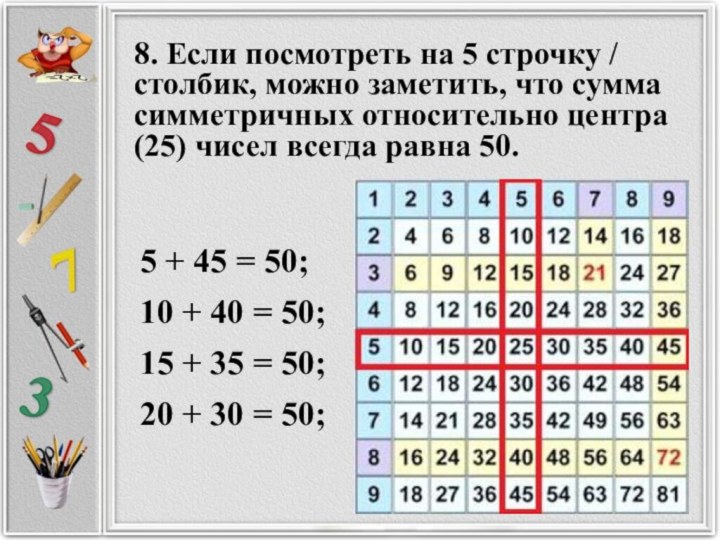
8. Если посмотреть на 5 строчку / столбик,
можно заметить, что сумма симметричных относительно центра (25) чисел
всегда равна 50.
5 + 45 = 50;
10 + 40 = 50;
15 + 35 = 50;
20 + 30 = 50;
Слайд 22
9. При умножении на 5 цифры
0 и 5
в разряде единиц чередуются:
5, 10, 15, 20, 25, 30,
35, 40, 45, 50.
Слайд 23
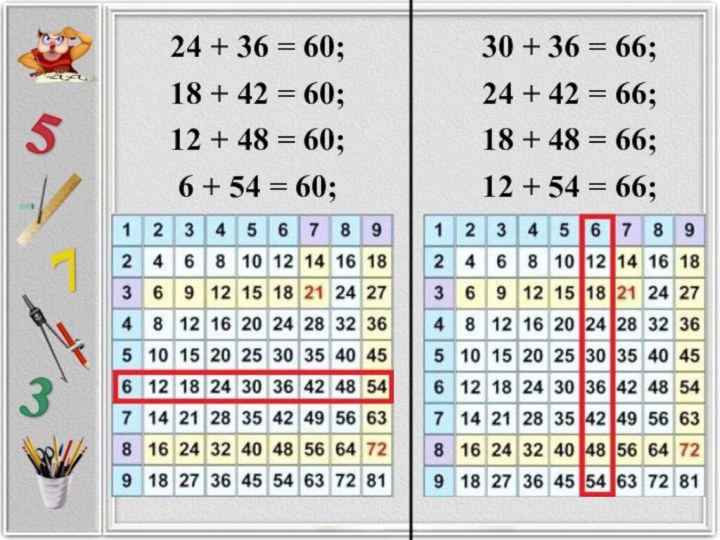
10. В 6-ой строчке числа
располагаются так, что
сумма
симметричных относительно
центра всегда равна 60, а в
6-ом
столбце сумма симметричных
относительно друг друга – 66.
Слайд 24
24 + 36 = 60;
18 + 42 =
60;
12 + 48 = 60;
6 + 54 = 60;
30
+ 36 = 66;
24 + 42 = 66;
18 + 48 = 66;
12 + 54 = 66;
Слайд 25
11. При умножении на 6 сумма
цифр всегда делится на 3:
1 х 6 =
6; 6 : 3;
2 х 6 = 12; (1 + 2) = 3 : 3;
3 х 6 = 18; (1 + 8) = 9 : 3;
4 х 6 = 24; (2 + 4) = 6 : 3;
5 х 6 = 30; (3 + 0) = 3 : 3;
6 х 6 = 36; (3 + 6) = 9 : 3;
7 х 6 = 42; (4 + 2) = 6 : 3;
8 х 6 = 48; (4 + 8) = 12 : 3;
9 х 6 = 54; (5 + 4) = 9 : 3;
Слайд 26
12. При умножении на 8 сумма
цифр произведения
уменьшается.
1 х 8 = 8; 8
2 х 8 =
16; 1 + 6 = 7
3 х 8 = 24; 2 + 4 = 6
4 х 8 = 32; 3 + 2 = 5
5 х 8 = 40; 4 + 0 = 4
6 х 8 = 48; 4 + 8 = 12; 1 + 2 = 3
7 х 8 = 56; 5 + 6 = 11; 1 + 1 = 2
8 х 8 = 64; 6 + 4 = 10; 1 + 0 = 1
Но: 9 х 8 = 72; 7 + 2 = 9.
Слайд 27
13. При умножении на 9 сумма цифр
произведения
всегда равна 9.
1 + 8 = 9
2 + 7
= 9
3 + 6 = 9
4 + 5 = 9
5 + 4 = 9
6 + 3 = 9
7 + 2 = 9
8 + 1 = 9
Слайд 28
14. При умножении на 9 результаты
симметричны относительно
друг
друга.
2 х 9 = 18;
9 х 9 = 81;
3 х 9 = 27; 8 х 9 = 72;
4 х 9 = 36; 7 х 9 = 63;
5 х 9 = 45; 6 х 9 = 54;
Слайд 29
Интересные способы запоминания таблицы умножения
Слайд 30
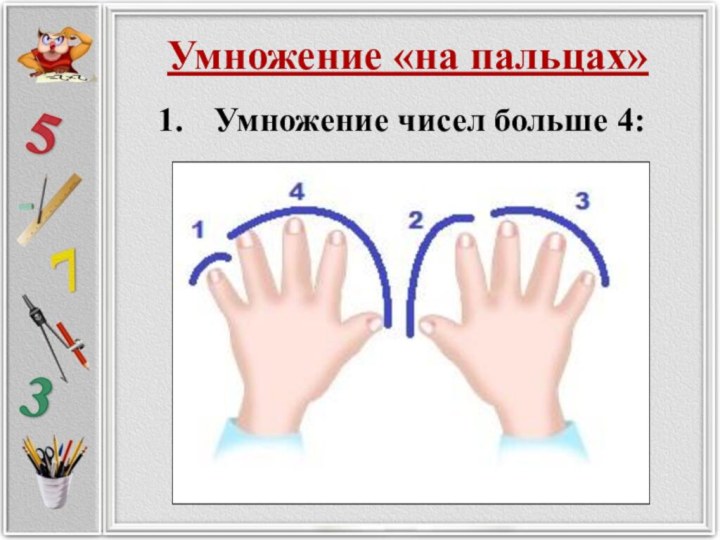
Умножение «на пальцах»
Умножение чисел больше 4:
Слайд 31
На левой руке загибается столько пальцев, на сколько
первый со-множитель превышает число 5;
На правой руке - столько
пальцев, на сколько второй сомножитель превышает число 5;
Складываем кол-во загнутых пальцев (получим число десятков);
Перемножаем кол-во незагнутых пальцев (получим число единиц).
Получаем число десятков и еди-ниц, т.е. полноценный результат умножения.
Слайд 32
Пример: 6 х 8
- На левой руке загибают
1 палец,
т.к. 6 – 5 = 1;
- На правой
руке загибают 3 пальца,
т.к. 8 – 5 = 3.
Складывают 1 и 3, получают 4
десятка.
Перемножают кол-во незагнутых
пальцев на левой (4) и правой (2)
руках: 4 х 2 = 8.
В результате получаем цифры
десятков и единиц – 4 дес. 8 ед. = 48.
Слайд 34
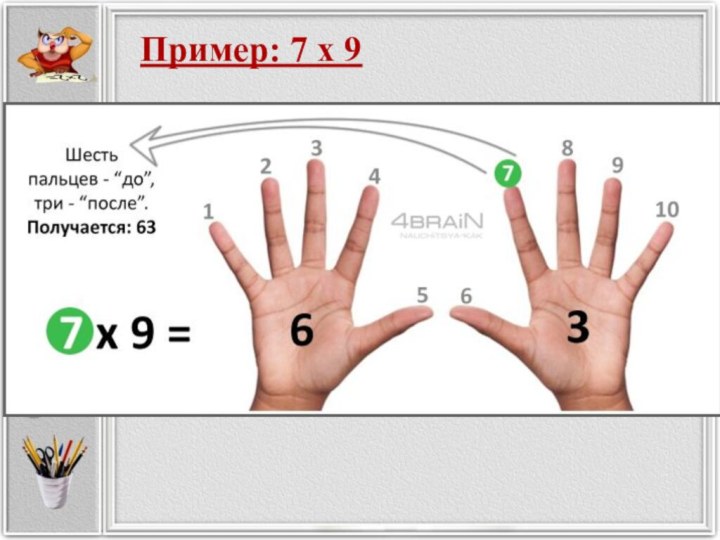
- Главным числом является то число, которое умножают
(число х).
- Положив руки перед собой, ученик должен отсчитать
слева направо х пальцев и загнуть этот палец.
- Кол-во пальцев справа от загнутого показывает количество единиц в результате умножения, а слева от согнутого – число десятков в результате.
Слайд 36
Таблица умножения в стихах
Андрей Усачев
книга-сборник
«Таблица
умножения в
стихах»
Слайд 39
Таблица умножения в песне
...
Трижды три навеки - девять,
Ничего
тут не поделать!
И нетрудно сосчитать,
Сколько будет пятью пять!
Пятью пять
- двадцать пять!
…
У кого, друзья, не спросим,
Шестью восемь - сорок восемь!
Шестью шесть - прошу учесть,
Неизменно тридцать шесть!
…