Презентация на тему к уроку математики Комбинаторика

1.2. Предмет теории вероятностей.
2. Математическая статистика.
2.1.

Предмет математической статистики.
3. Комбинаторика
3.1. Историческая справка.
3.2. Виды комбинаторных задач и способы их решения.
3.3. Решение комбинаторных задач в 5 классе.
3.4. Решение комбинаторных задач в 6 классе.
Заключение.
Список литературы.
Приложения.
Приложение 1.
Приложение 2.

является включение в него элементов

статистики
комбинаторики

теории

вероятностей

-
Без

минимальной вероятностно-статистической
грамотности трудно адекватно воспринимать социаль-
ную, политическую, экономическую информацию и
принимать на её основе обоснованные решения.

Практически все отрасли естествознания, весь комплекс
социально-экономических наук построены и развиваются
на вероятностно-статистической базе, и без соответствующей подготовки невозможно полноценное изучение этих дисциплин уже в средней школе.

Знание основ теории вероятностей ,случайных процессов и математической статистики необходимы в
настоящее время как инженеру практически любого
профиля, так и менеджеру и маркетологу, поскольку
серьёзный анализ рынка немыслим без владения
статистическими методами.

решение комбинаторных задач: перебор вариантов, подсчёт числа вариантов с помощью правила умножения;
представление данных в виде таблиц диаграмм ,графиков;
диаграммы Эйлера;
средние результатов измерений;
понятие и примеры случайных событий;
частота события, вероятность;
равновозможные события и подсчёт их вероятности;
представление о геометричес-
кой вероятности.

Министерство образования Российской Федерации
рекомендует ориентироваться на следующее содержание:

торики, статистики и теории вероятности начать
в 5-6

классах
или в 7 классе
в зависимости от системы изложения в учебнике.

середине 18 в.

Труды Б.Паскаля и П.Ферма соста-

вили основу теории вероятностей,
установили связь комбинаторного
анализа с теорией вероятности.

Первую книгу по теории вероятности
опубликовал Х.Гюйгенс.

Становление теории вероятностей как
математической науки связано с име-
нами Я. Бернулли, А.Муавра, П.Лапла-
са, К.Гаусса, С.Пуассона, П.Л.Чебышева,
А.А.Маркова, А.М.Ляпунова, Е.ЕСлуц-кого, А.Я.Хинчина, А.Н.Колмогорова, Б.В.Гнеденко, Н.Винера, Э.Бореля, В.Феллера и других.

мас-
совым случайным яв-
лениям.
Рассматриваются

не са
ми реальные явления,
А их упрощённые схе-
мы.

систематизации и обработки результатов наблюдений массовых слу- чайных явлений для

выявлений существующих закономерностей. Тесно связана с теорией вероятности . Предмет математической статистики- изучение случайных величин по результатам наблюдений.

различные сферы мысли к которым можно отнести все математические

идеи». Дж. Сильвестр (1844 г.)

Комбинаторными задачами в самом широком смысле этого слова

наполнена вся наша повседневная жизнь: рассаживая гостей за столом,

решая кроссворды, играя в карты, составляя какие-либо расписания,

открывая сейф с наборным замком, набирая номер телефона, мы решаем

комбинаторную задачу.

Э л е м е н т ы к о м б и н а т о р и к и.

числа. Ещё в 10 веке до нашей эры китайские математики

занимались изучением комбинаций и перестановок цифр.

Ло Шу - магический квадрат 3х3,
Р.Луллий - превратил комбинаторику в своего рода культ,
Б.Паскаль - создание теории азартных игр, рождение комбинаторики
П.Ферма как раздела науки,
Г.В.Лейбниц –ввёл термин «комбинаторика», мечтал о построении общей
комбинаторной теории,
Л.Эйлер -рассматривал задачи о разбиении чисел, о построении
магических и латинских квадратов,
Я.Бернулли -вывел формулы для числа перестановок n элементов, для
числа сочетаний и числа размещений с повторениями и без
повторений,
У.Гамильтон –придумал игру «Кругосветное путешествие» на поиск кратчай-
шего пути в графе,
Р.Киркман -поставил и решил задачу о 15 школьницах,
Дж.К.Рот –алгебраизация комбинаторики.
Р.Стенли
50-е годы -возрождение интереса к комбинаторному анализу в связи с бурным
20 века развитием кибернетики и широким использованием ЭВМ.
активизируется интерес к классическим комбинаторным задачам.
20-21век -решена комбинаторная задача под названием «проблема четырёх красок»

математики, посвящённый решению задач выбора и расположения элементов

некоторого , обычно конечного множества в соответствии с заданными правилами,
Каждое такое правило определяет способ построения некоторой конструкции
из элементов исходного множества, называемой комбинаторной конфигурацией.
Поэтому можно сказать, что целью комбинаторного анализа является изучение комбинаторных конфигураций.
Это изучение включает в себя вопросы существования комбинаторных конфигураций, алгоритмы их построения, оптимизацию таких алгоритмов, а также решение задач перечисления,в частности определение числа конфигураций данного класса.
Простейшими примерами комбинаторных конфигураций являются перестановки,
сочетания и размещения.

с задач, при решении которых требуется непосредственно составлять те

или иные комбинации и лишь после этого подсчитывать число возможных вариантов.
Здесь же разъясняются и формулируются основные правила комбинаторики-правило суммы и правило произведения.
Правило суммы .
Пример. Ученик должен выполнить практическую работу по математике. Ему предложили 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?

Правило произведения.
Пример. Сколько трёхзначных чисел можно составить из цифр 1, 3, 5, 7, используя в записи каждую из них не более одного раза?

их буквами а, в,с. Эти книги можно расставить на

полке по-разному: авс, асв,вас,вса, сав, сва. Каждое из этих расположений-называется перестановкой из трёх элементов.

Число перестановок из n элементов обозначается Рn, (читается «Р из n»).

Пример. Сколькими способами могут быть расставлены 8 участниц финального забега на восьми беговых дорожках?

Вводится понятие «факториал» и формула его нахождения.

Рn=n! n!=1х2х3х4х…хn -произведение первых n множителей.

Решение задачи: Р8=1х2х3х4х5х6х7х8=40320 способов расстановки.

шара и 3 пустых ячейки. Обозначим щары буквами а,в,с,d

В пустые ячейки можно по-разному разместить три шара из этого набора шаров:
асв, вас, авс.

Каждую упорядоченную тройку, которую можно составить из четырёх элементов
называют размещением из четырёх элементов по три.

Число размещений из n элементов по k обозначают Аn (читают «А из n по k»)

Пример. Учащиеся второго класса изучают 8 предметов. Сколькими способами составить расписание на один день, чтобы в нём было 4 различных предмета?

Речь идёт о размещении 8 предметов по 4.

Решение: 8х7х6х5=1680.

букетов, в которых по-разному сочетаются 3 гвоздики из данных

пяти гвоздик разного цвета.

Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных элементов.

Пример. На соревнования по лёгкой атлетике приехала команда из 12 спортсме-
нок. Сколькими способами тренер может определить, кто из них побежит в эстафете 4х100 на первом, втором, третьем, четвёртом этапах?

Решение. 12х11х10х9=11880 способов.

класс». Авторы: Н.Я. Виленкин, В.И.Жохов, А.С.Чесно- ков, С.И.Шварцбурд ).
Этой теме посвящены

следующие задания:
№ 11,58,59,96,132,165,197,
228,257. 283,322,324.388,
401,414,432,441,510,598,
694,733,775, 807, 835,
922,1035,1071.

Работа начинается с задач, в которых нужно найти все возможные комбинации и посчитать их количество.
Пример. Сколько трёхзначных чисел можно составить из цифр 3,5,7,
если в записи числа цифры не
будут повторяться?

№96. В правление фирмы вхо-
дят 5 человек. Из своего состава прав-
ление должно выбрать президента и
вице-президента. Сколькими способа-
Ми это можно сделать?
Составляется дерево возможных вариантов.
Вводится правило умножения.

Примеры задач:
Из села Аникеево в село Большово
ведут 4 дороги, а из села Большово
в село Виноградово-3 дороги.
Сколькими способами можно добраться из Аникеева в Виноградово череэ село Большово?

№694. Семье, состоящей из бабушки, папы, мамы, дочери
и сына, подарили 5 разных чашек.
Сколькими способами можно разде-
лить чашки между членами семьи?
Вводится термин «факториал»
и обозначение n!

горизонтальных или вертикальных полос разного цвета. Сколько могло бы

быть флагов, состоящих из 2 горизон-тальных полос разного цвета?
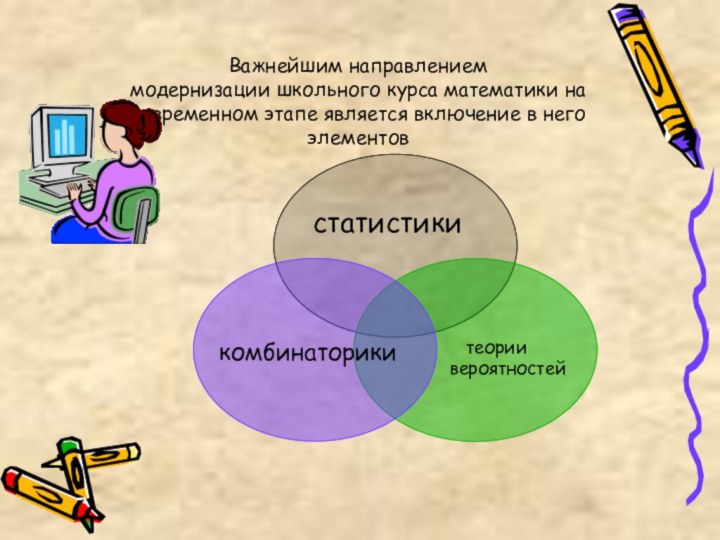
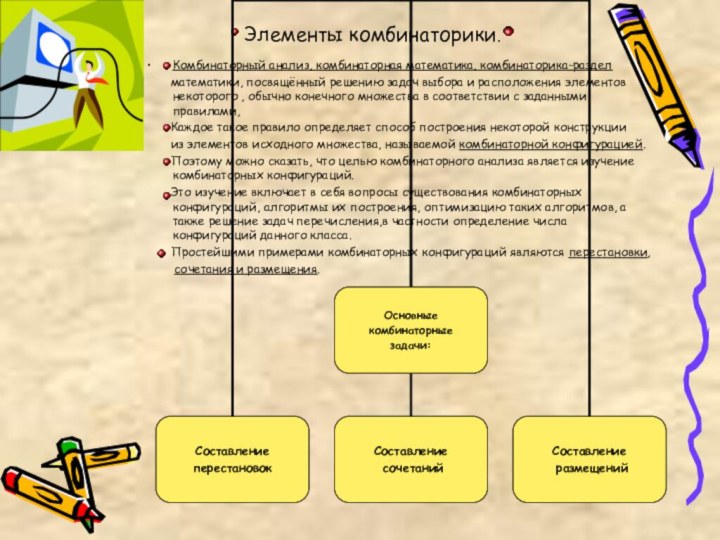
Вводится понятия «комбинаторика»,
«комбинаторные задачи».

№1220 Введение понятия «граф».
Ответьте на вопросы , используя
графы.
В спортивном зале собрались Витя, Коля, Петя, Серёжа и Максим.
Оказалось, что каждый из мальчиков
Знаком только с двумя другими.
Кто с кем знаком?

Примеры задач:
№53 На уроке физкультуры Андрей, Марат,
Костя, Саша, Серёжа готовятся к прыжкам в высоту.
Сколькими способами можно установить для них очерёдность
прыжков?

Этой теме посвящены следующие
задания:
№ 23,24,53,80,81,108,137,160,
194,232,262,355,410,462,1220,1249,
1303.

Решаем комбинаторные задачи в 6 классе. Учебник «Математика 6 класс» Авторы: Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков,С.И.Шварцбурд.

№137 Сколько чётных 4-значных чисел
можно составить из цифр 0,2,3,4,5?
№194 Сколько 3-значных чисел можно
Составить из чётных цифр?
№410 В городе 7-значные номера. Сколько может быть номеров,
начинающихся цифрами 235?

р а
1. Берлов С.А., Иванов С.В., С.В. Кохась

«Петербургские математические олимпиады»
Санкт-Петербург, Москва, Краснодар, »Лань» 2003;
2. Виленкин Н.Я., Жохов В.И.,Чесноков А.С., Шварцбурд С.И.
«Математика» 5 класс учебник для общеобразовательных учреждений
М. «Мнемозина» 2008;
3. Виленкин Н.Я., Жохов В.И.,Чесноков А.С., Шварцбурд С.И.
«Математика» 6 класс учебник для общеобразовательных учреждений
М. «Мнемозина» 2008;
4. Виноградов И.М. «Математическая энциклопедия»
М. «Советская энциклопедия» 1979
5. Гарднер Мартин «Математические досуги»
М «Оникс» 1995
6. Дорофеев Г.В. И др. «Математика 6 класс. Дидактические материалы»
М «Дрофа» 1995
7. Игнатьев Е.И. «В царстве смекалки»
М «Наука» 1979
8. Изучаем элементы статистики»
ж-л «Математика в школе» №5 2004
9. Когаловский С.Р. «Роль комбинаторных задач в обучении математике»
ж-л «Математика в школе» №7 2004
10. Козлова Е.Г. «Сказки и подсказки»
М МИРОС 1994

комбинаторику»
ж-л «Математика в школе» №8

2000;
12. Лысенко Ф.Ф. «Математика 5-6 класс. Тесты для промежуточной
аттестации» Ростов-на Дону «Легион» 2008;
13. Макарычев Ю.Н., Миндюк Н.Г.
«Элементы комбинаторики в школьном курсе алгебры»
ж-л «Математика в школе» №7 2003;
14.»О введении элементов комбинаторики, статистики и теории вероятностей
в содержание математического образования основной школы»
ж-л «Математика в школе» №9 2003;
15. Письменный Д.Т. «Конспект лекций по теории вероятностей, математи-
ческой статистике и случайным процессам»
М «Айрис-Пресс» 2008;
16. Романова Н.В. «Комбинаторно-геометрическо- арифметические задачи
на стыке начальной и основной школ»
ж-л «Математика в школе» №4 2004;
17. Студенецкая В.Н., Фадеева О.М. «Статистика и теория вероятностей
на пороге основной школы»
ж-л «Математика в школе» №5 2004;
18. Интернет.