- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему моих учеников к уроку математике на тему Рисунки на координатной Плоскости
Содержание
- 2. История возникновения координатЗа 200 лет до нашей
- 3. Восточную долготу и северную широту обозначают числами
- 4. Долгое время лишь география "землеописание" - пользовалась
- 5. На основе этого удачного нововведения возник метод
- 6. Широта – параллели,долгота - меридианыСистема географических координатНанесенные
- 7. Практическая значимость Определение координатов из жизни например,
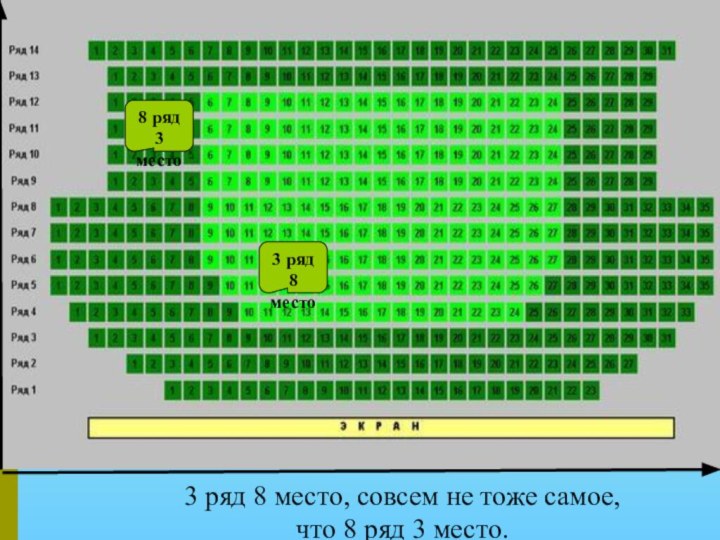
- 8. Чтобы найти свое место в зале,сначала мы ищем свой ряд, затем своё место.
- 9. 3 ряд 8 место, совсем не тоже самое,что 8 ряд 3 место.3 ряд8 место8 ряд3 место
- 10. Чтобы найти свое место в поезде сначала мы ищем свой вагон, затем номер своего места.
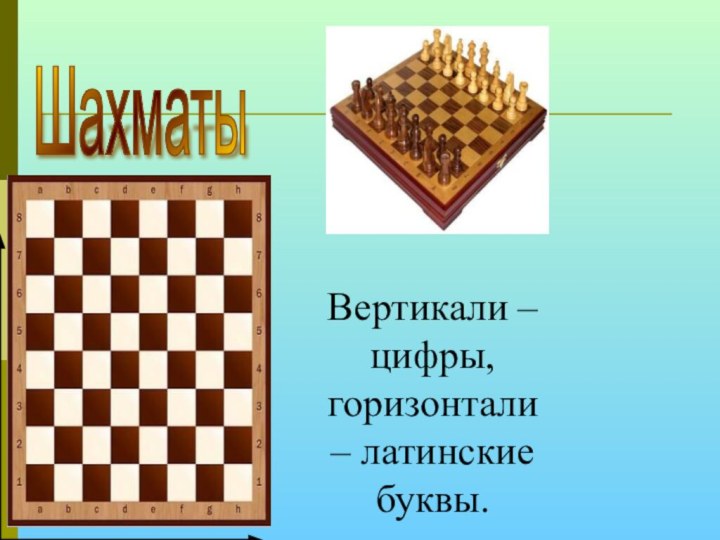
- 11. Шахматы Вертикали – цифры,горизонтали – латинские буквы.
- 12. А какие красивые рисунки можно нарисовать, используя координатную плоскость!?
- 13. Координатная плоскость / рисунокУХ01-8188-101 (-1;-6)2 (1;2)3 (3;2)4
- 14. Координатная плоскость / рисунокУХ01-8188-101 (-1;-6)2 (1;2)3 (3;2)4
- 15. хy011(3;0) (1;2) (-1;2) (2;5) (1;7) (-3;6)
- 16. хy011(3;0) (1;2) (-1;2) (2;5) (1;7) (-3;6)
- 17. (3;3) (0;3) (-3;2) (-5;2) (-7;4) (-8;3)
- 18. © Кузьмина Е.А., Колобовская МСОШ, 2011
- 19. (1;-4) (1;-6) (-4;-6) (-3;-5) (-1;-5) (-3;-4)
- 20. (1;-4) (1;-6) (-4;-6) (-3;-5) (-1;-5) (-3;-4)
- 21. Скачать презентацию
- 22. Похожие презентации
История возникновения координатЗа 200 лет до нашей эры греческий ученый Гиппарх ввёл географические координаты. Он предложил нарисовать на географической карте параллели и меридианы и обозначить числами широту и долготу. С помощью этих двух чисел можно точно










Слайд 3 Восточную долготу и северную широту обозначают числами со
знаком «плюс», а западную долготу и южную широту —
со знаком «минус». Таким образом, пара чисел со знаками однозначно определяет точку на земном шаре.Например, пара +70° , +60° определяет точку в центре острова Вайгач, расположенного в Карском море.
У писателя Жюля Верна, некоторые романы построены на ситуациях, связанных с географическими координатами. Это романы «Удивительные приключения дядюшки Антифера» и «Дети капитана Гранта».
Слайд 4
Долгое время лишь география "землеописание" - пользовалась этим
замечательным изобретением, и только в 14 веке французский математик
Никола Орсем (1323-1382) попытался приложить его к "землеизмерению" - геометрии. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.
Слайд 5
На основе этого удачного нововведения
возник метод координат,
связавший геометрию с алгеброй. Основная заслуга в создании этого
метода принадлежит великому французскому математику Рене Декарту (1596 - 1650). В его честь такая система координат называется декартовой, обозначающая место любой точки плоскости расстояниями от этой точки до "нулевой широты" - оси абсцисс " и "нулевого меридиана" - оси ординат.По традиции, введенной Декартом, "широта" точки обозначаются буквой x, "долгота" - буквой "y".
Слайд 6
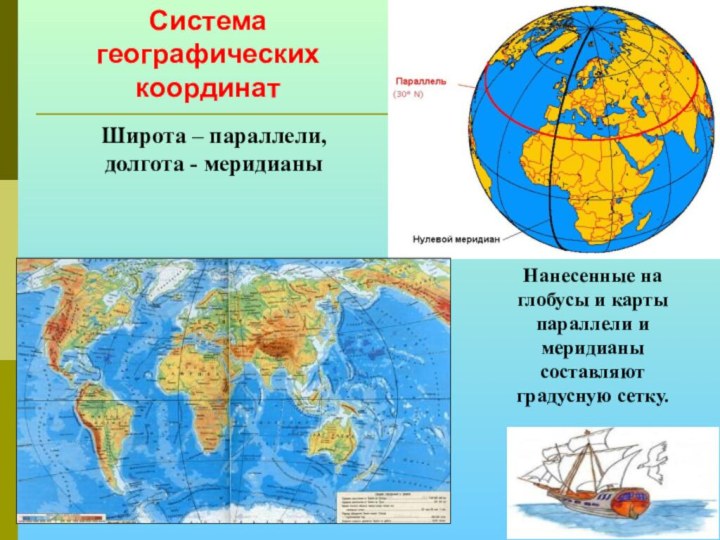
Широта – параллели,
долгота - меридианы
Система географических координат
Нанесенные на
глобусы и карты параллели и меридианы составляют градусную сетку.
Слайд 7
Практическая значимость
Определение координатов из жизни например, на
билете в кинотеатр стоят два числа: ряд и место
— их можно рассматривать как координаты места в зале.Подобные координаты приняты о шахматах. Вместо одного из чисел берется буква: вертикальные ряды клеток обозначаются буквами латинского алфавита, а горизонтальные — цифрами. Таким образом, каждой клетке шахматной доски ставится в соответствие пэра из буквы и числа, и шахматисты получают возможность записывать свои партии.
Также эта система используется и в поездах, что бы найти своё место в поезде.
Слайд 13
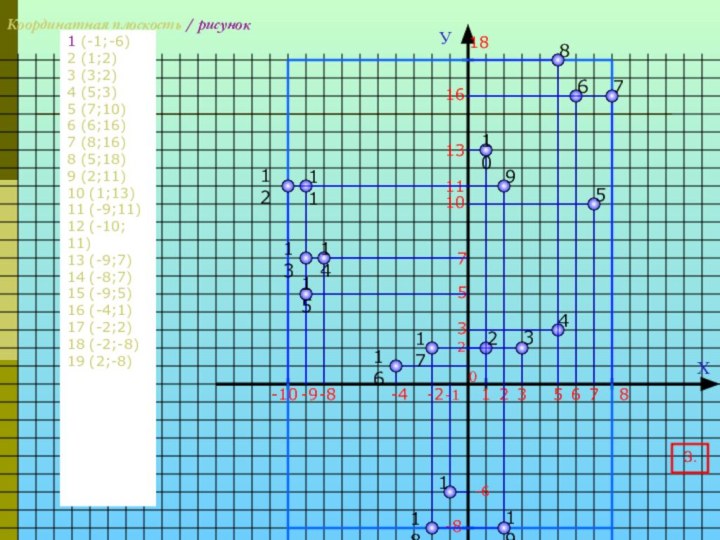
Координатная плоскость / рисунок
У
Х
0
1
-8
18
8
-10
1 (-1;-6)
2 (1;2)
3 (3;2)
4 (5;3)
5
(7;10)
6 (6;16)
7 (8;16)
8 (5;18)
9 (2;11)
10 (1;13)
11 (-9;11)
12 (-10; 11)
13
(-9;7)14 (-8;7)
15 (-9;5)
16 (-4;1)
17 (-2;2)
18 (-2;-8)
19 (2;-8)
-1
-6
1
2
2
3
19
3
5
3
4
7
10
5
16
6
2
6
7
8
11
9
13
10
-9
11
12
7
13
-8
14
5
15
-4
16
-2
17
18
З.
Слайд 14
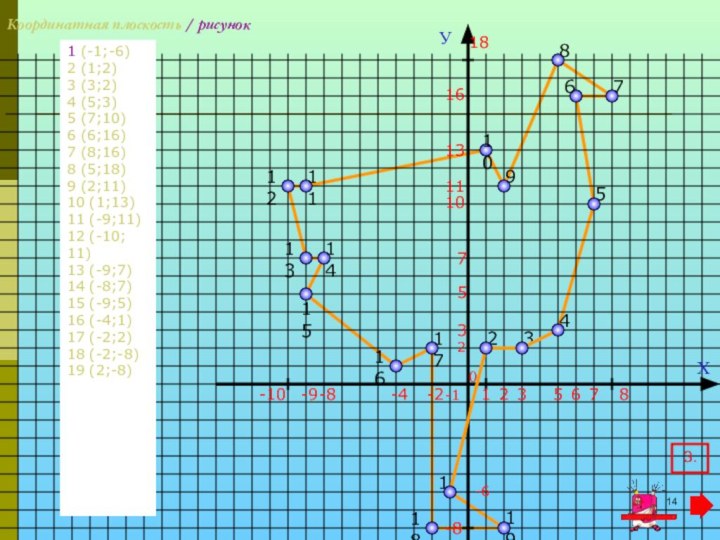
Координатная плоскость / рисунок
У
Х
0
1
-8
18
8
-10
1 (-1;-6)
2 (1;2)
3 (3;2)
4 (5;3)
5
(7;10)
6 (6;16)
7 (8;16)
8 (5;18)
9 (2;11)
10 (1;13)
11 (-9;11)
12 (-10; 11)
13
(-9;7)14 (-8;7)
15 (-9;5)
16 (-4;1)
17 (-2;2)
18 (-2;-8)
19 (2;-8)
-1
-6
1
2
2
3
19
3
5
3
4
7
10
5
16
6
2
6
7
8
11
9
13
10
-9
11
12
7
13
-8
14
5
15
-4
-2
17
18
16
З.
Слайд 15
х
y
0
1
1
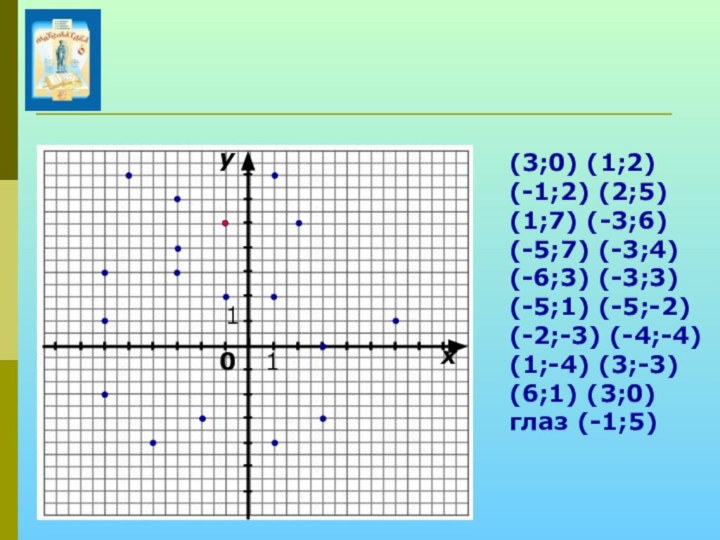
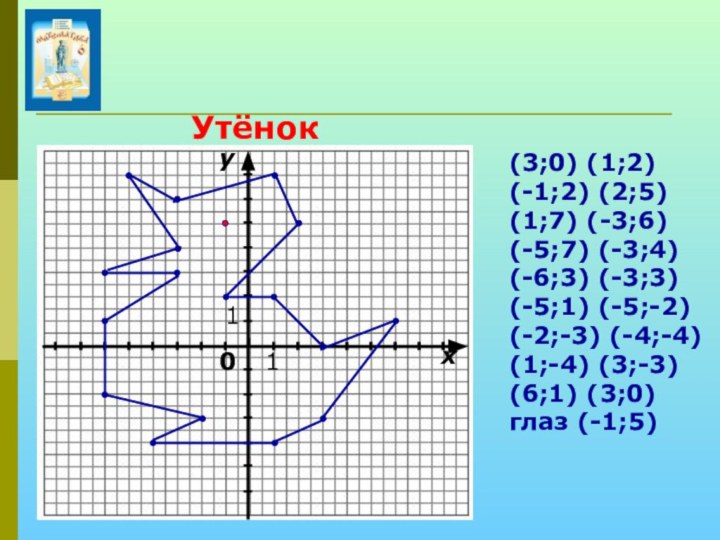
(3;0) (1;2) (-1;2) (2;5) (1;7) (-3;6)
(-5;7) (-3;4) (-6;3) (-3;3) (-5;1) (-5;-2) (-2;-3) (-4;-4) (1;-4)
(3;-3) (6;1) (3;0) глаз (-1;5)
Слайд 16
х
y
0
1
1
(3;0) (1;2) (-1;2) (2;5) (1;7) (-3;6)
(-5;7) (-3;4) (-6;3) (-3;3) (-5;1) (-5;-2) (-2;-3) (-4;-4) (1;-4)
(3;-3) (6;1) (3;0) глаз (-1;5)
Утёнок
Слайд 17
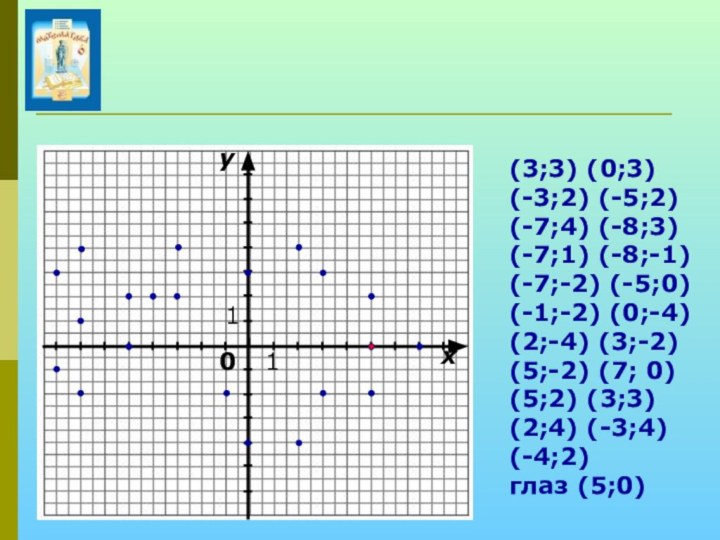
(3;3) (0;3) (-3;2) (-5;2) (-7;4) (-8;3)
(-7;1) (-8;-1) (-7;-2) (-5;0) (-1;-2) (0;-4) (2;-4) (3;-2) (5;-2)
(7; 0) (5;2) (3;3) (2;4) (-3;4) (-4;2) глаз (5;0)
Слайд 18
© Кузьмина Е.А., Колобовская МСОШ, 2011
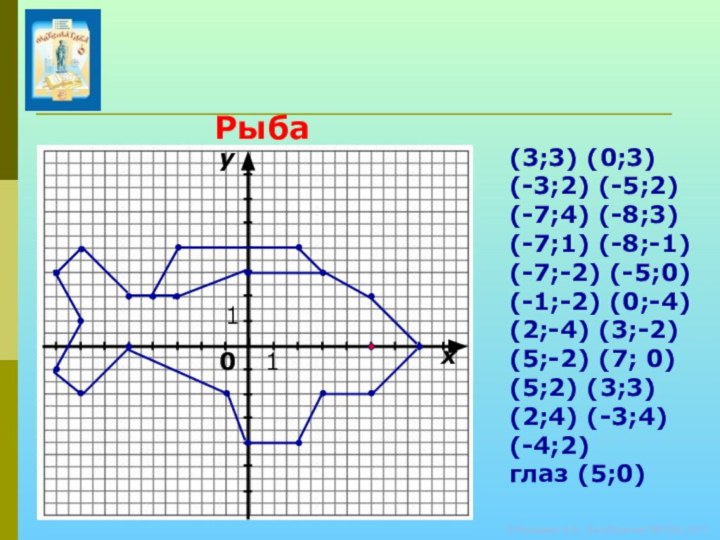
Рыба
(3;3) (0;3) (-3;2) (-5;2) (-7;4) (-8;3) (-7;1) (-8;-1) (-7;-2) (-5;0) (-1;-2) (0;-4) (2;-4) (3;-2) (5;-2) (7; 0) (5;2) (3;3) (2;4) (-3;4) (-4;2) глаз (5;0)
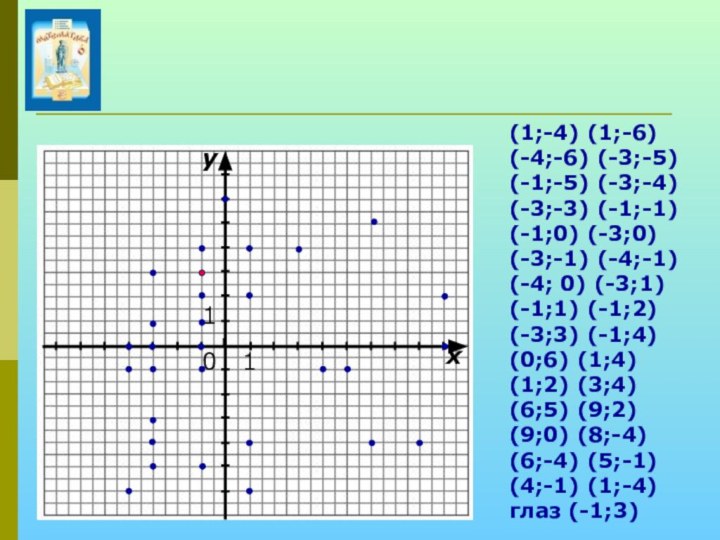
Слайд 19 (1;-4) (1;-6) (-4;-6) (-3;-5) (-1;-5) (-3;-4)
(-3;-3) (-1;-1) (-1;0) (-3;0) (-3;-1) (-4;-1) (-4; 0)
(-3;1) (-1;1) (-1;2) (-3;3) (-1;4) (0;6) (1;4) (1;2) (3;4) (6;5) (9;2) (9;0) (8;-4) (6;-4) (5;-1) (4;-1) (1;-4) глаз (-1;3)
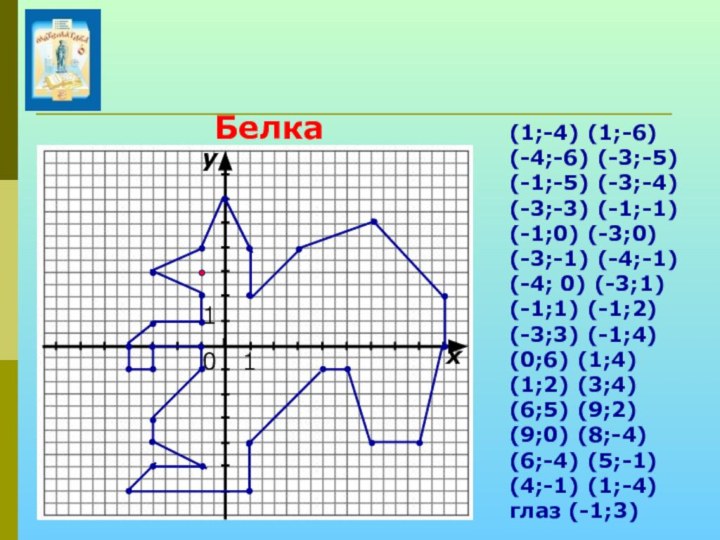
Слайд 20 (1;-4) (1;-6) (-4;-6) (-3;-5) (-1;-5) (-3;-4)
(-3;-3) (-1;-1) (-1;0) (-3;0) (-3;-1) (-4;-1) (-4; 0)
(-3;1) (-1;1) (-1;2) (-3;3) (-1;4) (0;6) (1;4) (1;2) (3;4) (6;5) (9;2) (9;0) (8;-4) (6;-4) (5;-1) (4;-1) (1;-4) глаз (-1;3)
Белка