до прямой
Расстояния от точки до плоскости
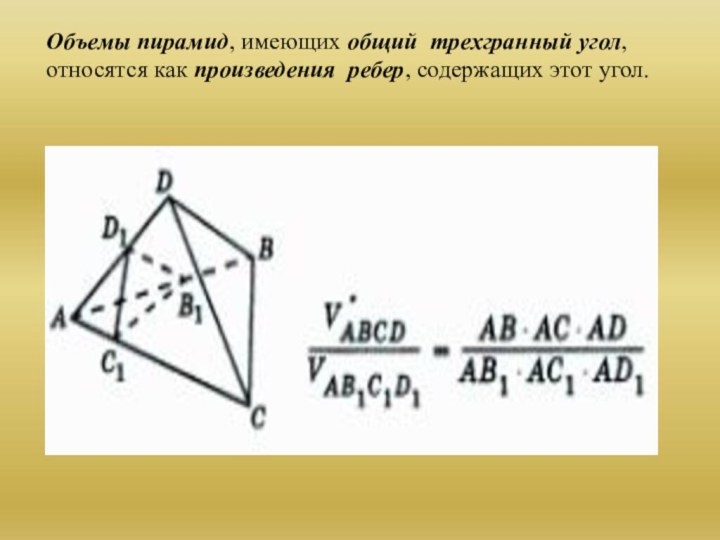
Расстояния между скрещивающимися прямыми
Угла
между двумя прямымиУгла между прямой и плоскостью
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





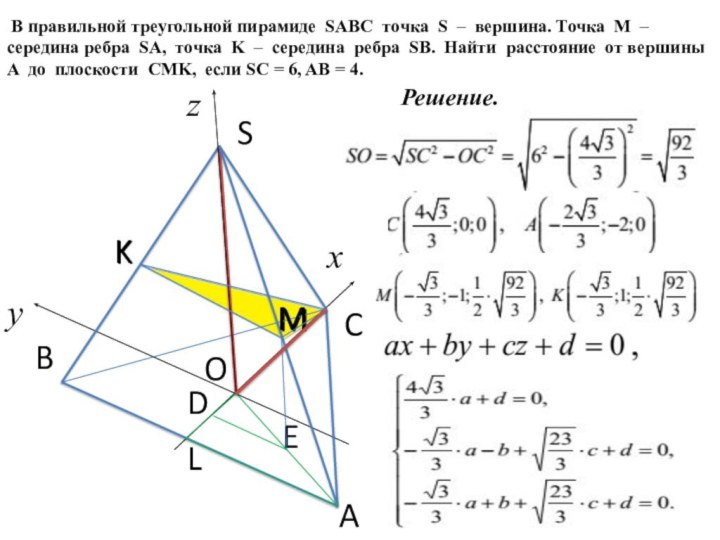
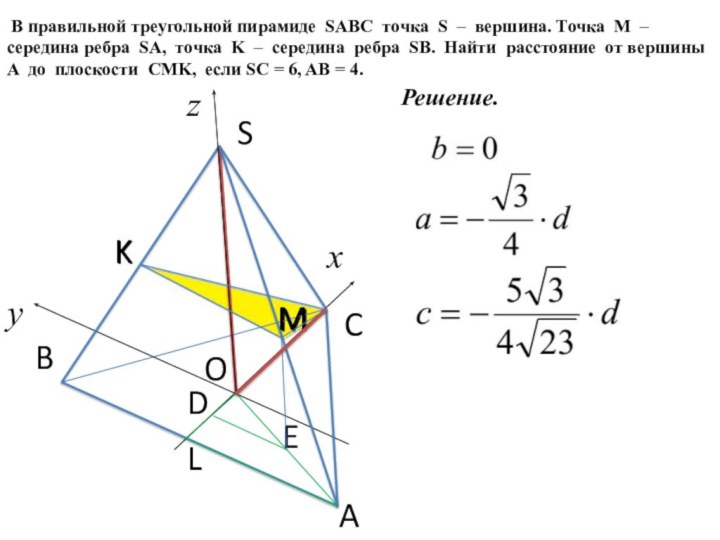
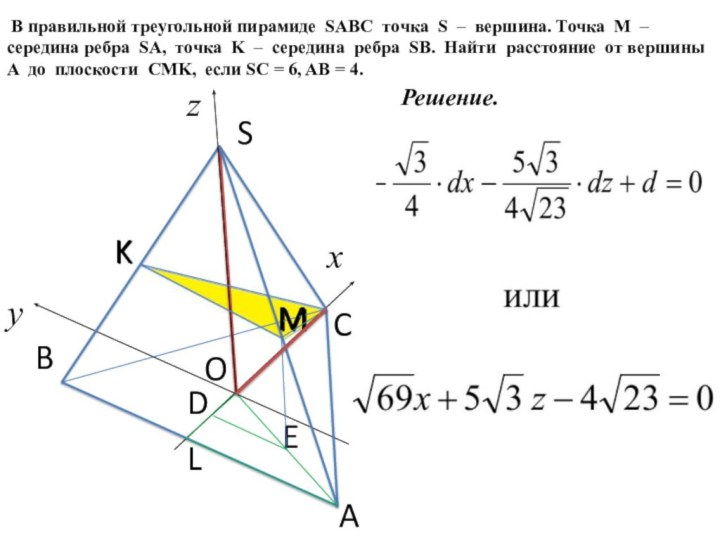
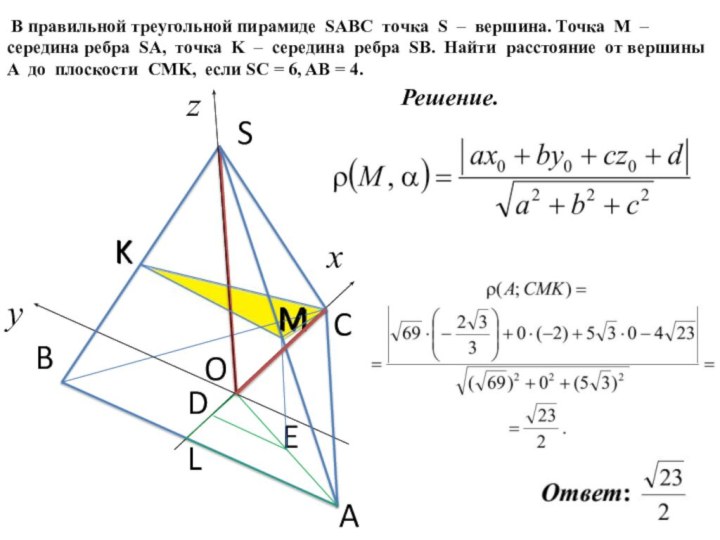
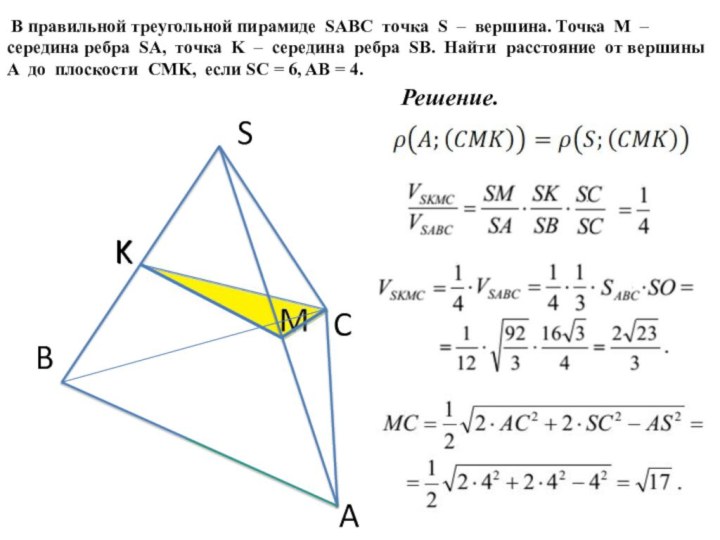
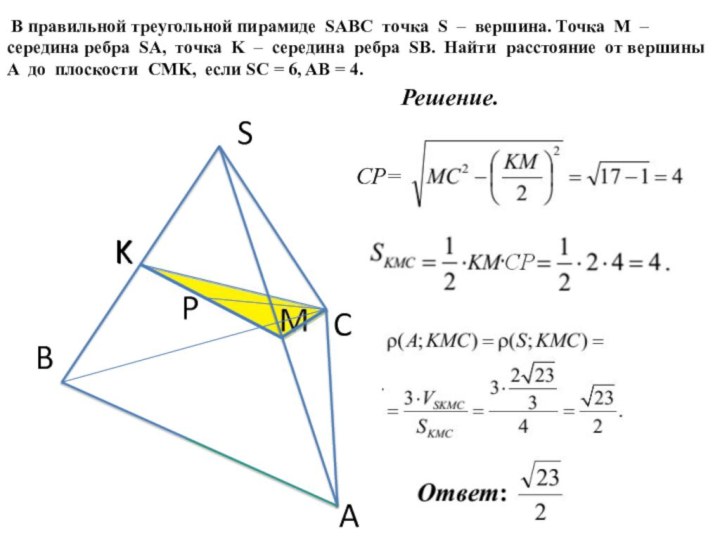


Решение.
K
Решение.
K
Решение.
K
Решение.
K
A
B
C
О
М
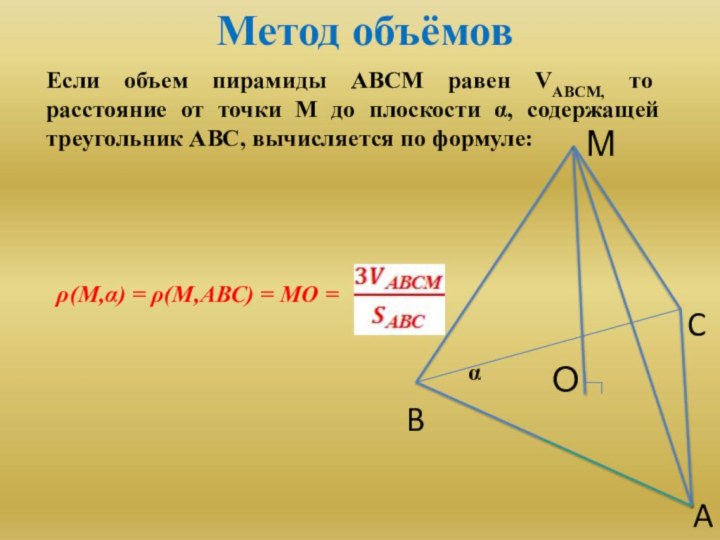
ρ(М,α) = ρ(М,АВС) = МО =
α
Решение.
K
Решение.
K
P
CP=
Решение.
K
P
H
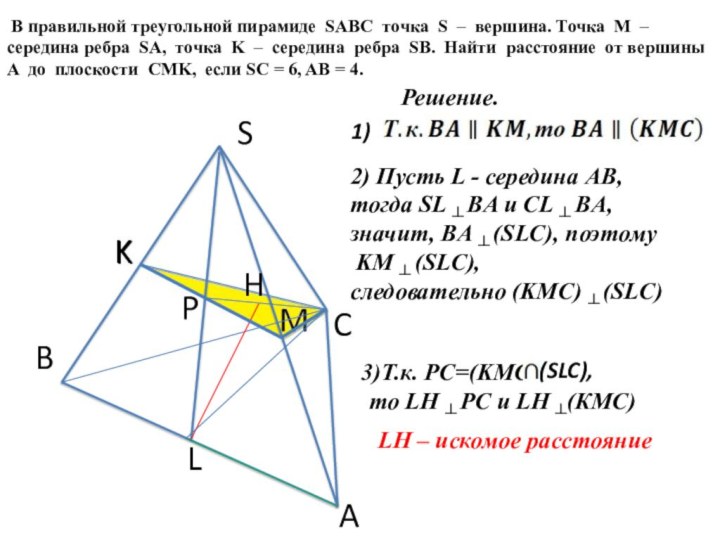
1)
2) Пусть L - середина AB,
тогда SL ┴ BA и CL ┴ BA,
значит, BA ┴ (SLC), поэтому
KM ┴ (SLC),
следовательно (KMС) ┴ (SLC)
3)Т.к. РС=(KMС)
то LН ┴ РС и LН ┴(КМС)
(SLC),
LH – искомое расстояние
Решение.
О
P
H
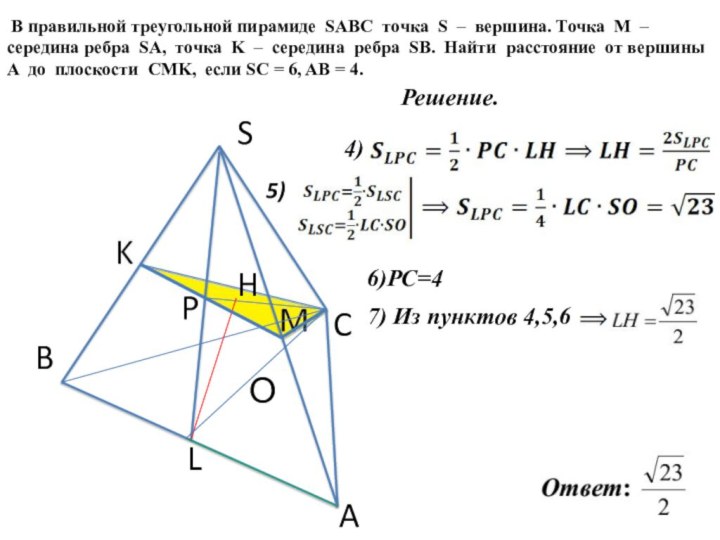
4)
5)
6)PC=4
7) Из пунктов 4,5,6