Слайд 2
Тригонометрия – слово греческое и в
буквальном переводе означает измерение треугольников (trigwnon - треугольник, а
metrew- измеряю).
Возникновение тригонометрии связано с землемерием, астрономией и строительным делом.
Слайд 3
Впервые способы решения треугольников, основанные на зависимостях между
сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом
(2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.).
Слайд 4
Позднее зависимости между отношениями сторон треугольника и его
углами начали называть тригонометрическими функциями.
Слайд 5
Тригонометрические сведения были известны древним вавилонянам и египтянам,
но основы этой науки заложены в Древней Греции.
Слайд 6
Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии,
связанные с астрономией. Однако они рассматривали не линии синуса,
косинуса и др., а хорды. Греческое слово "хорда", означает "тетива лука". Первые таблицы хорд дошли до нас в книге Птолемея "Альмагест"
(II в. н.э.)
Слайд 7
В IV веке центр развития математики переместился в
Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо
знакомы с трудами греческих астрономов и геометров.
Слайд 8
Чистой геометрией индийцы интересовались мало, но их вклад
в прикладную астрономию и расчётные аспекты тригонометрии очень значителен.
Слайд 9
Замену античных хорд на синусы
(sinus –изгиб,
кривизна)
в прямоугольном треугольнике провели индийские математики.
Слайд 10
Слово косинус намного моложе. Косинус – это сокращение
латинского выражения completely sinus, т. е. “дополнительный синус” (или
иначе “синус дополнительной дуги”).
Слайд 11
Название «тангенс», происходящее от латинского tanger (касаться), переводится
как «касающийся» (линия тангенсов – касательная к единичной окружности).
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке Аль – Батани, который составил таблицы синусов и тангенсов.
Слайд 12
Однако эти открытия долгое время оставались неизвестными европейским
ученым, и тангенсы были заново открыты лишь в XIV
веке немецким математиком, астрономом Региомонтаном (1467 г.). Именно он доказал теорему тангенсов
Слайд 13
Развитие тригонометрии в Новое время(XVI – XVII век)
стало чрезвычайно важным не только для астрономии и астрологии,
но и для других приложений, в первую очередь артиллерии, оптики и навигации при дальних морских путешествиях.
Слайд 14
Поэтому после XVI века этой темой занимались многие
выдающиеся учёные, в том числе Николай Коперник, Иоганн Кеплер, Франсуа Виет.
Слайд 15
В России первые сведения о тригонометрии были опубликованы
в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению
мудролюбивых тщателей», опубликованном при участии Л. Ф. Магницкого в 1703 году.
Слайд 16
В 1714 году появилось содержательное руководство «Геометрия практика»,
первый русский учебник по тригонометрии.
Слайд 17
Современный вид тригонометрии придал Леонард Эйлер. В трактате «Введение
в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций,
эквивалентное современному.
Слайд 18
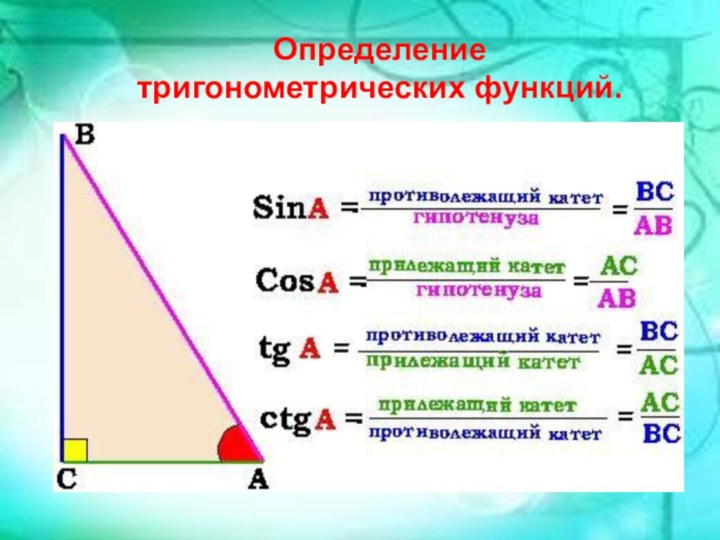
Определение тригонометрических функций.