Слайд 2
Научиться считать!
Во все времена математика была и остается
одним из основных предметов в школе, потому что математические
знания необходимы всем людям. Не каждый школьник, обучаясь в школе, знает, какую профессию он выберет в будущем, но каждый понимает, что математика необходима для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. Кроме того, всем школьникам необходимо сдавать экзамены в 9-м классе и в 11-м классе, а для этого, обучаясь с 1-го класса, необходимо качественно осваивать математику и прежде всего, нужно научиться считать.
«Счет и вычисления – основы порядка в голове»
Иоганн Генрих Песталоцци (1746 - 1827)
Слайд 3
Актуальность проекта
Актуальность исследования
состоит в том, что в наше время все
чаще на помощь ученикам приходят калькуляторы, и многие из них просто не умеет считать устно. Это снижает качество знаний по очень важному предмету, снижает интерес к изучению математики. Допустить этого нельзя! Ведь изучение математики развивает логическое мышление, память, гибкость ума, приучает человека к точности, к умению видеть главное.
Поэтому я хочу научиться быстро считать сам и помочь в этом моим одноклассникам.
Слайд 4
Цель проекта:
изучить методы и приемы
быстрого счета
и показать необходимость их эффективного использования.
Слайд 5
Задачи проекта:
изучить историю возникновения вычислений
рассмотреть правила вычислений, которыми
пользовались в древности и которыми пользуются сейчас,
освоить правила
быстрого счета и научить пользоваться ими учащихся нашего класса.
создать памятку о наиболее полезных для школьников приёмах быстрого счёта.
оформить альбом «Приемы быстрого счета»
Слайд 6
Гипотеза исследования.
Если показать, что применение
приемов быстрого счета, облегчает вычисления, то можно добиться того,
что повысится вычислительная культура учащихся, и им будет легче решать практические задачи.
Объект исследования: различные алгоритмы счета
Предмет исследования: процесс вычислений.
Субъект исследования: учащиеся 5 класса.
Слайд 7
История возникновения чисел
У древних людей, кроме
каменного топора и шкуры вместо одежды, ничего не было,
поэтому считать им было нечего. Постепенно они стали приручать скот, возделывать поля; появилась торговля, и тут уж без счета никак не обойтись.
Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги.
Слайд 8
Древние шумеры.
Первыми придумали запись чисел древние шумеры.
Они пользовались всего двумя цифрами.
Вертикальная черточка обозначала одну
единицу, а угол из двух лежачих черточек – десять.
Эти черточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки.
Слайд 9
Древний народ майя.
Древний народ майя вместо самих
цифр рисовал страшные головы,
как у пришельцев,
и отличить
одну голову – цифру от другой было очень сложно.
Слайд 10
История возникновения чисел
Индейцы и народы Древней Азии
при счете завязывали узелки на шнурках разной длины и
цвета.
У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают четыре узелочка на красном шнурке
Слайд 11
Древние индийцы.
Было очень неудобно хранить глиняные таблички, веревки
с узелками и рулоны папируса.
И это продолжалось
до тех пор, пока древние индийцы не изобрели
для каждой цифры свой знак.
Вот как они выглядели
Слайд 12
История возникновения чисел
От пальцевого счета пошли пятеричная
система счисления (одна рука), десятеричная (две руки), двадцатеричная (пальцы
рук и ног).
В древние времена не существовало единой для всех стран системы счета. Некоторые системы исчисления брали за основу 12, другие – 60, третьи – 20, 2, 5, 8.
Слайд 13
История возникновения чисел
Десятичную систему счисления ввели римляне.
Римские цифры до сих пор используют в часах и
для оглавления книг, но такая система цифр тоже была слишком сложной для счета.
Предки русского народа – славяне - для обозначения чисел употребляли буквы.
Этот способ обозначения цифр называется цифирью.
Слайд 14
Старинные способы быстрого счета
Русский крестьянский способ умножения
Пример:
умножим
47 на 35,
запишем числа на одной строчке, проведём между
ними вертикальную черту;
левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
деление заканчивается, когда слева появится единица;
вычёркиваем те строчки, в которых стоят слева чётные числа;
далее оставшиеся справа числа складываем – это результат;
35 + 70 + 140 + + 280 + 1120 = 1645.
Слайд 15
Метод «решетки»
(Абу Абдалах Мухаммед Бен Мусса аль
– Хорезми)
Метод решетки:
Найдем произведение чисел 25 и 63.
Горизонтально
запишем числа 25,
вертикально 63.
Чертим решетку, проводим диагонали.
На пересечениях находим
произведения чисел.
Складываем
числа по диагоналям.
Получили результат: 1575
Слайд 16
Египетский способ умножения
Обозначения чисел, которые использовались в древности,
были более или менее пригодны для записи результата счета.
А вот выполнять арифметические действия с их помощью было очень сложно, особенно это касалось действия умножения (попробуй, перемножь: ξφß*τδ).
Выход из этой ситуации нашли египтяне, поэтому способ получил название египетского.
Пример: 34 ∙ 5=(30+4)5=30*5+4*5=150+20=170.
Слайд 17
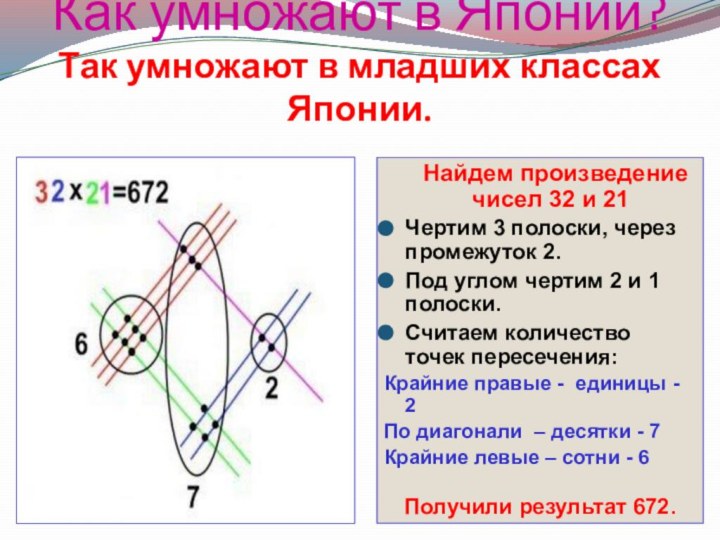
Как умножают в Японии?
Так умножают в младших классах
Японии.
Найдем произведение чисел 32 и 21
Чертим
3 полоски, через промежуток 2.
Под углом чертим 2 и 1 полоски.
Считаем количество точек пересечения:
Крайние правые - единицы - 2
По диагонали – десятки - 7
Крайние левые – сотни - 6
Получили результат 672.
Слайд 18
Система Трахтенберга
Яков Трахтенберг
еврейско-русский математик, который, находясь в заключении в фашистском
концлагере во время Второй мировой войны, разработал систему быстрого счета. Занимался он этим, чтобы сохранить рассудок. Система Трахтенберга позволяет умножать большие числа на небольшие.
Слайд 19
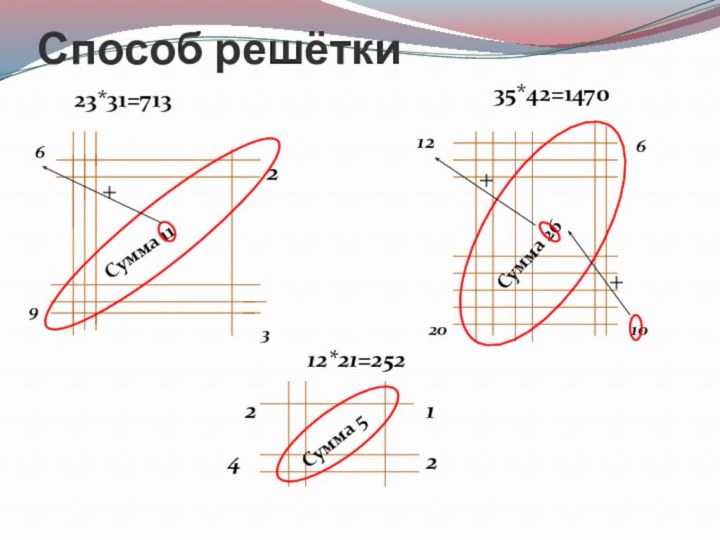
Способ решётки
23*31=713
6
2
9
3
35*42=1470
12
6
20
10
12*21=252
2
1
4
2
Сумма 11
Сумма 26
Сумма 5
+
+
+
Слайд 20
Умножение на двенадцать
(по Трахтенбергу).
Правило умножения
на 12: нужно удваивать поочередно каждую цифру и прибавлять
к ней поочередно ее «соседа».
Пример: 63247 · 12
Необходимо записывать цифры множимого через интервал и каждую цифру результата писать точно под цифрой числа 63247, из которой она образовалась.
63247 · 12 1дважды 7 будет = 14, переносим
4
63247 · 12 дважды 4+7+1=16, переносим 1
64
63247 · 12 дважды 2+4+1 = 9
964
Следующие шаги аналогичны.
Окончательный ответ:
63247 · 12 = 758964
Слайд 21
Египетский способ умножения
Заменить умножение на любое число -
удвоением, то есть сложением числа с самим собой.
Пример:
34
∙ 5 = 34∙ (1 + 4) =
= 34 ∙ 1+ 34 ∙ 4.
Т. к. 5 = 4 + 1, то для получения ответа оставалось сложить числа, стоящие в правом столбике против цифр 4 и 1 , т. е.
136 + 34 = 170.
Слайд 22
Прием перекрестного умножения
при действии с двузначными числами
Древние греки и индусы в старину называли его
«способом молнии» или «умножение крестиком»
Пример:
24 ∙ 32 = 768
Последовательно производим следующие действия:
4 ∙ 2 = 8 – это последняя цифра результата.
2 ∙ 2 = 4; 4 ∙ 3 = 12; 4 + 12 = 16.
6 – предпоследняя цифра в ответе, единицу запоминаем.
2 ∙ 3 = 6, 6 + 1 = 7 – это первая цифра в ответе.
Ответ: 768.
Слайд 23
Счёт на пальцах
Способ быстрого умножения чисел в пределах
первого десятка на 9.
Допустим, нам нужно умножить 7
на 9.
Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева).
Число пальцев слева от загнутого будет равно десяткам, а справа - единицам искомого произведения.
Слайд 24
Сложение с использованием свойств действий с числами
Сложение с
использованием свойств действий с числами
Слагаемые разбивают на такие группы,
которые в сумме дают круглые числа:
12+63+28=(12+28)+63=40+63=103.
Если одно слагаемое близко к круглому числу, то его заменяют разностью и дополнением между круглым числом:
549+94= (500+100)+(49-6)=600+43=643.
Если оба слагаемых близки к круглому числу, то они заменяются разностью между круглым числом и дополнением:
504+497=(500+500)+(4–3)=1000+1=1001.
Слайд 25
Способы быстрого сложения и вычитания натуральных чисел
Если вычитаемое
уменьшить на несколько единиц и уменьшаемое увеличить на столько
же единиц, то разность не изменится.
Пример:
529 – 435 = (529 - 5) - (435+5) = 524 – 440 = 84
Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц.
Пример:
785 + 963 = 785 + (963+7) – 7 = 785 + 970 – 7= = 1748
Слайд 26
Применение свойств вычитания
Если из числа вычесть сумму чисел,
можно сначала вычесть из этого числа одно слагаемое, а
затем, из полученной разности второе слагаемое:
934 – (123 + 634)= (934 – 634) – 123 = 300 – 123 = 177
Если из суммы чисел вычесть число, можно вычесть его из одного слагаемого и затем к полученной разности прибавить второе слагаемое:
(567 + 148) – 367 = (567 - 367) +148 = 200 +148 = 348
Слайд 27
Способ быстрого вычитания
Поразрядное вычитание:
Если число единиц каждого
разряда уменьшаемого больше, то вычитаем поразрядно и результаты складываем.
Пример1:
574-243=(500-200)+(70-40)+(4-3)=300+30+1=331.
Если меньше, то занимаем у высшего разряда:
Пример 2:
647–256=(500-200)+(140-50)+(7-6)=300+90+1=391.
Слайд 28
Умножение чисел от 10 до 20
Чтобы найти произведение
чисел
от 10 до 20 необходимо:
к одному
из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.
Пример 1. 16∙18 = (16+8) ∙ 10 + 6 ∙ 8 = 288,
Пример 2. 17 ∙ 19 = (17+9) ∙ 10 + 7 ∙ 9 = =323.
Слайд 29
Умножение на 11
Чтобы двузначное число, сумма цифр
которого не превышает 10, умножить на 11, надо цифры
этого числа раздвинуть и поставить между ними сумму этих цифр.
Примеры:
72 ∙ 11 = 7 (7 + 2) 2 = 792;
35 ∙ 11 = 3 (3 + 5) 5 = 385.
Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
Пример:
94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034.
Слайд 30
Умножение на 4
Чтобы устно умножить
число на 4, его дважды удваивают. Например:
287*4 =574*2=1148
335*4 =
670*2 =1340
Слайд 31
Умножение на 22, 33, ..., 99
Чтобы двузначное число
умножить на
22, 33, ..., 99, надо:
этот множитель
представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть
44 = 4 · 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11.
Пример 1:
24 ∙ 22 = 24 ∙ 2 ∙ 11 = 48 ∙ 11 = 528
Пример 2.
23 ∙ 33 = 23 ∙ 3 ∙ 11= 69 ∙ 11 = 759
Слайд 32
Умножение на 5, на 50, на 25, на
125
При умножении на эти числа можно воспользоваться следующими
выражениями:
a ∙ 5 = a ∙ 10 : 2 a ∙ 50 = a ∙ 100 : 2
a ∙ 25 = a ∙ 100 : 4 а ∙ 125 = а ∙1000:8
1. 17 ∙ 5 = 17 ∙ 10:2 = 170:2 = 85
2. 43 ∙ 50 = 43 ∙ 100:2 = 4300:2 = 2150
3. 27 ∙ 25 = 27 ∙ 100:4 = 2700:4 = 675
4. 96 ∙ 125 = 96:8 ∙ 1000 = 12 ∙ 1000 = 12000
Слайд 33
Умножение на 5; 50; 0,5;0,25
Чтобы умножить число на
5, нужно умножить его на 10 и разделить на
2:
138 · 5 = (138 · 10) : 2 = 1380 : 2 = 690.
Чтобы умножить число на 50, нужно умножить его на 100 разделить на 2:
87 · 50 = (87 · 100) : 2 = 4350.
Чтобы умножить число на 0,5, нужно разделить его на 2:
360 · 0,5 = 360:2=180.
Чтобы умножить число на 0,25, нужно разделить его на 4:
280 · 0,25 = 280 : 4 = 70
Слайд 34
Умножение на 125; 12,5; 1,25; 0,125
Чтобы умножить число
на 125, нужно умножить его на 1000 и разделить
на 8:
32 · 125 = 32 : 8 · 1000 = 4000.
Чтобы умножить число на 12,5, нужно умножить его на 100 и разделить на 8:
24 · 12,5 = 24 : 8 · 100 = 300.
Чтобы умножить число на 1,25, нужно умножить его на 10 и разделить на 8:
64 · 1,25 = 64 : 8 ·10 = 80.
Чтобы умножить число на 0,125, нужно разделить его на 8.
16,8 · 0,125=16,8 : 8 = 2,1.
Слайд 35
Умножение на 1,5; 2,5; 3,5 …
Чтобы умножить число
на 1,5, надо к данному числу прибавить его половину:
16·1,5
= 16+8= 10+14=24
Чтобы умножить число на 2,5, надо умножить его на два и прибавить половину числа:
16·2,5 = 16·2 + 8 = 32+8= 40
Чтобы умножить число на 3,5, надо умножить его на 3 и прибавить половину числа:
16·3,5 = 16·3+8=48+8 = 40+16=56
и т.д.
Слайд 36
Умножение на число, оканчивающиеся на 5
Чтобы четное двузначное
число умножить на число, оканчивающееся на 5, можно применить
следующее правило.
Если один из сомножителей увеличить в несколько раз, а другой уменьшить во столько же раз, произведение не изменится.
Примеры:
44 ∙ 5 = (44 : 2) ∙ 5 ∙ 2 = 22 ∙ 10 = 220;
28 ∙ 15 = (28 : 2) ∙ 15 ∙ 2 = 14 ∙ 30 = 420;
32 ∙ 25 = (32 : 2) ∙ 25 ∙ 2 = 16 ∙ 50 = 800.
Слайд 37
Умножение на число, оканчивающиеся на 5
При умножении на
65, 75, 85, 95 числа следует брать небольшие, в
пределе второго десятка. Если возьмем произвольное число (четное), тогда придется потрудиться и перемножить двузначные числа:
Примеры:
48 ∙ 65 = (48 : 2) ∙ 65 ∙ 2 = 24 ∙ 130 = (24 ∙ 10 + 24 ∙ 3) ∙ 10 = (240 + 72) ∙ 10 = 312 ∙ 10 = 3120;
36 ∙ 85 = (36 : 2) ∙ 85 ∙ 2 = 18 ∙ 170 = (18 ∙ 10 + 18 ∙ 7) ∙ 10 = (180 + 126) ∙ 10 = 306 ∙ 10 = 3060.
Слайд 38
Умножение на 25 чисел, делящихся на 4
ПРИЗНАК ДЕЛИМОСТИ НА 4
На 4 делятся те числа, у которых две последние цифры делятся на 4. Например:
1716 делится на 4, так как 16 делится на 4;
1800 делится на 4, так как 1 00 делится на 4.
Чтобы число умножить на 25, надо это число разделить на 4 и умножить на 100.
Примеры:
484 * 25 = (484 : 4) * 100 = 121 * 100 = 12 100;
124 *25 =124 : 4 *100 =3100.
Слайд 39
Возведение в квадрат чисел, оканчивающихся на 5
Чтобы возвести в квадрат: число десятков
умножаем на
следующее число стоящее в натуральном ряду и приписываем 25
Слайд 40
Возведение в квадрат чисел, оканчивающихся на 5
(2*3)25
6 25
(4*5)25
20 25
252=625
452=2025
Чтобы возвести в квадрат: число десятков умножаем на
следующее число стоящее в натуральном ряду и приписываем 25
Слайд 41
Способы быстрого деления
Последовательное деление
Если делитель является составным
числом, то разлагаем его на два или большее число
множителей, а потом выполняем последовательное деление:
720:45=(720:9):5=80:5=16,
9324:36=(9324:9):4=1036:4=259
945:35 = (945:5):7 = 179:7 = 27
Слайд 42
Деление на 5, на 50, на 25
При делении на 5, на 50, на 25 воспользуемся
следующими выражениями:
a : 5 = a ∙ 2 : 10
a : 50 = a ∙ 2 : 100
a : 25 = a ∙ 4 : 100
135 : 5 = 135 ∙ 2 : 10 = 270 : 10 = 27
3750 : 50 = 3750 ∙ 2 : 100 = 7500 : 100 =75
6400:25 = 6400 ∙ 4 : 100 = 25600 : 100 = 256
Слайд 43
Деление на 0,5; 0,25; 0,125
Чтобы разделить число на
0,5, нужно это число умножить на 2:
32 : 0,5
= 32 · 2 = 60 + 4 = 64
Чтобы разделить число на 0,25, нужно это число умножить на 4:
32 : 0,25 = 32 · 4 = 120 + 8 = 128
Чтобы разделить число на 0,125, нужно это число умножить на 8:
32 : 0,125 = 32 · 8 = 240 + 16 = 256
Слайд 44
Способы быстрого умножения и деления натуральных чисел
Для получения
единиц произведения перемножают единицы множителей,
для получения десятков умножают
десятки одного на единицы другого множителя и наоборот и результаты складывают,
для получения сотен перемножают десятки.
Пример. 62∙58 = 3596
а) 8 ∙ 2 = 16, пишем 6 помним 1.
б) 8 ∙ 6 + 5 ∙ 2 + 1= 59, пишем 9, помним 5.
в) 5 ∙ 6 + 5 = 35.
Слайд 45
Умножение чисел, у которых число десят-ков одинаковое, а
сумма единиц равна 10
Число десятков любого множителя умножить
на число, которое больше на 1, затем перемножить отдельно единицы этих чисел и, наконец, к первому результату справа приписать второй.
Пример.
204 ∙ 206 = 42024
20 ∙ (20+1) = 420, пишем 420
6 ∙ 4 = 24, пишем 24
Слайд 46
Возведение в квадрат числа, оканчивающегося на 5
Чтобы возвести в квадрат двузначное число, оканчивающееся на
5, нужно цифру десятков умножить на цифру, большую на единицу, и к полученному произведению приписать справа число 25
Примеры:
35² = 3·(3+1), приписать 25, получим 35²= 1225
75² = 7·8 , приписать 25 , 75² = 5625
85² = 8·925 = 7225
45² = 2025
Слайд 47
Возведение в квадрат числа, начинающегося на 5
Для возведения
в квадрат двузначного числа, начинающегося на пять, нужно прибавить к
25 вторую цифру числа и приписать справа квадрат второй цифры, причем если квадрат второй цифры – однозначное число, то перед ним надо приписать цифру 0.
Примеры:
56² = (25+6), приписать 6² =36, 56² = 3136
58² = (25+8), приписать 8² = 64, 58² = 3364
53²= (25+3), приписать 3² = 09, 53² = 2809
Слайд 48
Без карандаша и бумаги
Немецкого ученого Карла Гаусса
называли королем математики.
Его математическое дарование проявилось уже в
детстве. Рассказывают, что в трехлетнем возрасте он удивлял своего отца.
Однажды в школе, Гауссу в то время было 10 лет, учитель предложил классу перечислить все числа от 1 до 100. Пока он диктовал задание, у Гаусса был готов ответ :
1+2+3+…..+97+98+99+100=101·50=5050.
Как он складывал числа от 1 до 100?
Группируем: (1+100)+(2+99)+….=50 пар по 101,
а сумма S=101·50
Слайд 49
Угадывание задуманного числа
Предложите своим друзьям задумать любые числа.
Пусть каждый прибавит к своему задуманному числу 5.
Полученную сумму
пусть умножит на 3.
От произведения пусть отнимет 7.
Из полученного результата пусть вычтет ещё 8.
Листок с окончательным результатом пусть каждый отдаст вам. Глядя на листок, вы тут же говорите каждому, какое число он задумал.
(x+5 ) · 3 - 7- 8 = 3x +15 – 15 = 3x
Чтобы угадать задуманное число, результат, написанный на бумажке или сказанный вам устно, разделить на
Слайд 50
Легко запомнить!
11·11 =121
111·111=12321
1111·1111=1234321
11111·11111=123454321
------------------------
111111111·111111111=
=12345678987654321
Слайд 51
Картина Н.П. Богданова-Бельского «Устный счёт»
Картина Н.П. Богданова-Бельского «Устный
счёт» была написана в 1895 г., то есть более
110 лет назад.
Посмотрите, как сосредоточенно думает мальчик, изображенный на переднем плане. Видно, нелегкую задачу дал учитель. Но этот ученик, наверно, скоро закончит работу, ошибки не должно быть: уж очень серьезно относится он к устному счету. А тот, который что–то шепчет на ухо учителю, кажется, уже решил задачу, только его ответ не совсем правильный. Смотрите: учитель слушает ученика внимательно, но на лице нет одобрения, значит, ученик сделал что–то не так. А может, учитель терпеливо ожидает, когда и другие сосчитают, и потому не спешит одобрить ответ?
А какую же задачу дал им учитель? Не сможем решить ее и мы?
Слайд 52
Картина Н.П. Богданова-Бельского «Устный счёт»
Художник изобразил на этой
картине невыдуманных учеников и учителя. Учитель – Сергей Александрович
Рачинский, известный русский педагог, замечательный представитель русских образованных людей позапрошлого века. Он был доктором естественных наук и профессором ботаники Московского университета. В 1868 г. С. А. Рачинский решает «уйти в народ». Он держит экзамен на звание учителя начальных классов. На свои средства открывает школу для крестьянских детей в селе Татево Смоленской губернии и становится в ней учителем. Его ученики так хорошо считали устно, что этому удивлялись все посетители школы. Не случайно, художник изобразил С. А. Рачинского вместе с его учениками именно на уроке устного решения задач.
Эта картина - гимн учителю и ученику!
Слайд 53
Диагностика вычислительных навыков
Практическая часть включает в
себя изучение динамики развития вычислительных навыков. Была выдвинута следующая
гипотеза: с помощью приемов быстрого счета можно улучшить вычислительные навыки.
Объект исследования: 5 класс.
Время проведения: октябрь - декабрь.
Этапы исследования:
Изучить известные способы быстрого устного счета;
Подобрать материал для тренинга;
Провести диагностику;
Подвести результаты исследования
Слайд 54
Диагностика навыков счета
Для диагностики был составлен
ряд однотипных упражнений, состоящих из 24 примеров на сложение,
вычитание, деление и умножение, которые нужно было выполнить за 5 минут устно.
Этапы диагностики:
Проверка имеющихся навыков устного счета;
Изучение способов быстрого сложения и вычитания;
Знакомство с новыми приемами умножения;
Изучение способов быстрого деления.
Повторная проверка умения считать устно.
Фестиваль «Приемы быстрого счета»
Итоговая проверка вычислительных навыков.
Слайд 56
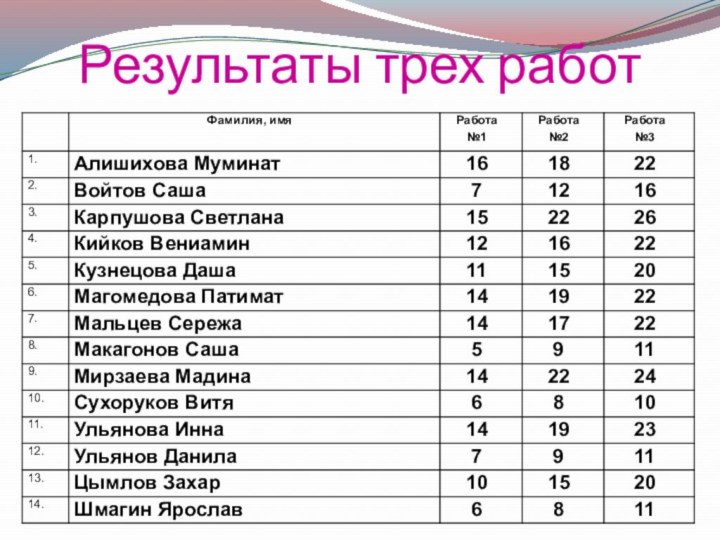
Результаты трех работ
Средний балл первой работы –
10,1
Средний балл второй работы – 15,3
Средний балл итоговой
работы – 20,6
Таким образом, мы видим, что наша первоначальная гипотеза о том, что знание и использование приемов быстрого счета позволит существенно увеличить скорость и качество счета, подтверждается
Слайд 57
Результаты работы:
изучили историю возникновения вычислений
рассмотрели правила
вычислений, которыми пользовались в древности и которыми пользуются сейчас
освоили
правила быстрого счета и научили пользоваться ими учащихся нашей школы.
провели фестиваль «Приемы быстрого счета» для учащихся 5 – 8 классов.
создали памятку о наиболее полезных для школьников приёмах быстрого счёта.
оформили альбом «Приемы быстрого счета»
Слайд 58
Гимнастика ума
Существуют способы быстрого сложения, вычитания, умножения, деления,
возведения в степень …
Используя некоторые из этих методов на
уроках или дома можно развить скорость вычислений, добиться успехов в изучении всех школьных предметов.
Умножение без калькулятора – тренировка памяти и математического мышления
Устный счет – гимнастика ума!
Нам было интересно работать над проектом. Пока мы только изучали и анализировали уже известные способы быстрого счета.
Но кто знает, возможно, в будущем мы сами сможем открыть новые способы быстрых вычислений!