- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Монотонность функции, экстремумы
Содержание
- 2. Функция y = f(x) убывает на промежутке,
- 3. Определение промежутков монотонности по графику (двигаясь слева
- 4. Теорема:Если функция f(x) дифференцируема на интервале (a;
- 5. Промежутки возрастания и убывания функции называют промежутками
- 6. Точка х0 называется точкой максимума функции f(x),
- 7. Точка х0 называется точкой минимума функции f(x),
- 8. Теорема:Пусть функция f(x) дифференцируема на интервале (a;
- 10. Скачать презентацию
- 11. Похожие презентации
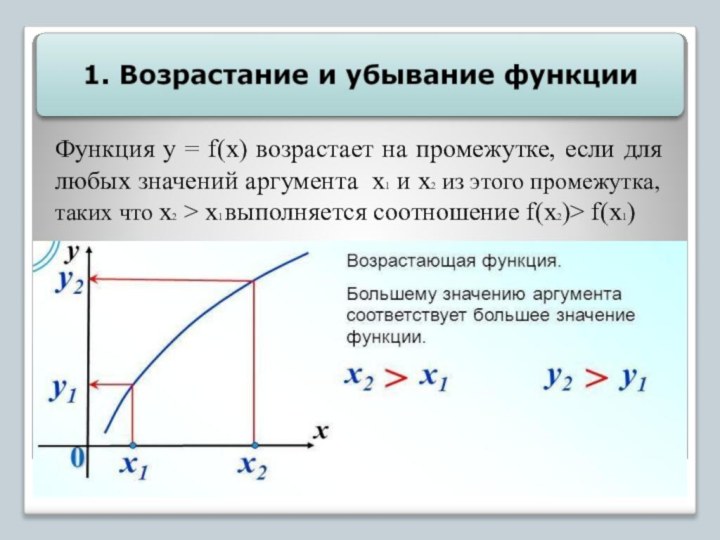
Функция y = f(x) убывает на промежутке, если для любых значений аргумента х1 и х2 из этого промежутка, таких что х2 > х1 выполняется соотношение f(х2)< f(х1)








Слайд 3
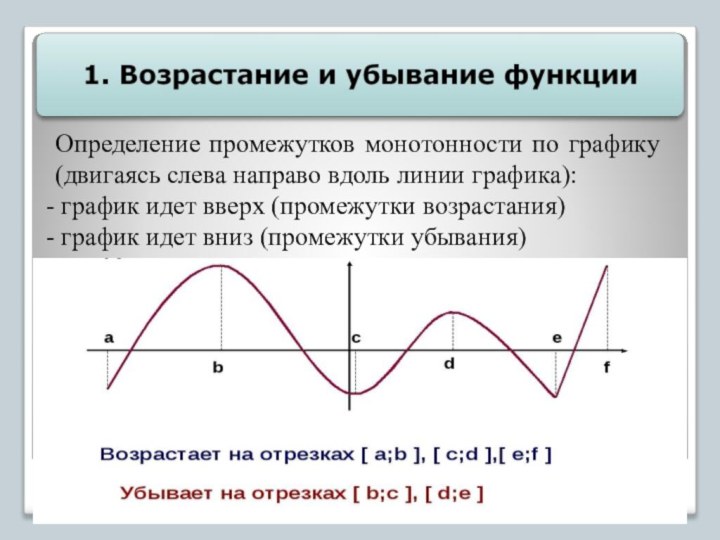
Определение промежутков монотонности по графику (двигаясь слева направо
вдоль линии графика):
график идет вверх (промежутки возрастания)
график
идет вниз (промежутки убывания)
Слайд 4
Теорема:
Если функция f(x) дифференцируема на интервале (a; b)
и fʹ(x)>0 для всех х (a; b), то
функция возрастает на промежутке (a; b)Если функция f(x) дифференцируема на интервале (a; b) и fʹ(x)<0 для всех х (a; b), то функция убывает на промежутке (a; b)
Слайд 5
Промежутки возрастания и убывания функции называют промежутками монотонности
функции
Пример: Найти промежутки монотонности функции
1.
2.
Слайд 6
Точка х0 называется точкой максимума функции f(x), если
существует такая окрестность точки х0, что для всех х
≠ х0 из этой окрестности выполняется неравенство f(х0)>f(x)
Слайд 7
Точка х0 называется точкой минимума функции f(x), если
существует такая окрестность точки х0, что для всех х
≠ х0 из этой окрестности выполняется неравенство f(х0)
Слайд 8
Теорема:
Пусть функция f(x) дифференцируема на интервале (a; b),
х0 (a; b) и fʹ(x0)=0. Тогда
если при
переходе через стационарную точку х0 функции f(x) ее производная меняет знак с “+” на “–”, то х0 – точка максимума функцииесли при переходе через стационарную точку х0 функции f(x) ее производная меняет знак с “–” на “+”, то х0 – точка минимума функции