Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Логарифмическая функция

Содержание

Цели урока:«Обобщить и закрепить понятие логарифмической функции, её свойства; свойства логарифма; закрепить умения применять эти понятия при решении уравнений, неравенств в целях подготовки к ЕГЭ ».
Урок – повторение. Тема : Логарифмическая функция.Учителя математикиМОУ СОШ № 73Антиповой Е.В. Цели урока:«Обобщить и закрепить понятие логарифмической функции, её свойства; свойства логарифма; Свойства логарифмовЛогарифмическая функция её свойства и график.Графический диктант.Определение логарифмаЛогарифмические уравнения.Логарифмические неравенства. Свойства логарифмовЛогарифм единицы.Логарифм самого основания.Логарифм произведения.Логарифм частного.Логарифм степени. Задания на применение свойств логарифмов . Найдите х: lg x=lg 3+2lg Определение логарифма 1.Найдите выражения, имеющие смысл :Log35, log50, log2(-4), log51, log55 .2.Найдите Графический диктант 1.Логарифмическая функция y=log a x определена при любом x. 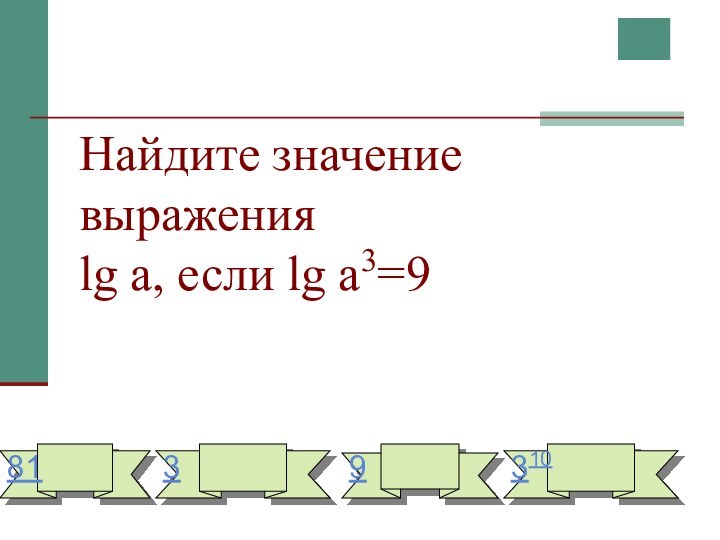Ответы:^-^-^-^-^-^-^-14 правильных ответов – «5»10-14 правильных ответов – «4»7-9 Возрастающая функцияY=log a x , x>0.При а>1 – функция возрастающая.Log 2 x < 2;Log 2x Убывающая функцияY=log a x ,x>0,При 0 Логарифмические уравнения.Log2(x+1) + log2(x+3) = 3;О.Д.З:X>-1,X>-3;Log2((x+1)(x+3)) = 3;Log2((x+1)(x+3)) = log2 8;(x+1)(x+3) = Решение неравенств.Log3(x+2)0: x>-2.Log3(x+2) Найдите значение выражения lg a, если lg a3=98139310 Неверное решение!Подумайте ещё! Вы выполнили задание верно! Найдите область определения функции y=log0,5( 25-x2)(-∞;-5]U[5;+∞) (-5;5) [-5;5](-∞;-5)U(5;+∞)? Найдите сумму корней уравненияLog2 (x2 – 1)=log2(3x(x – 1))11/2Нет корней3/2? 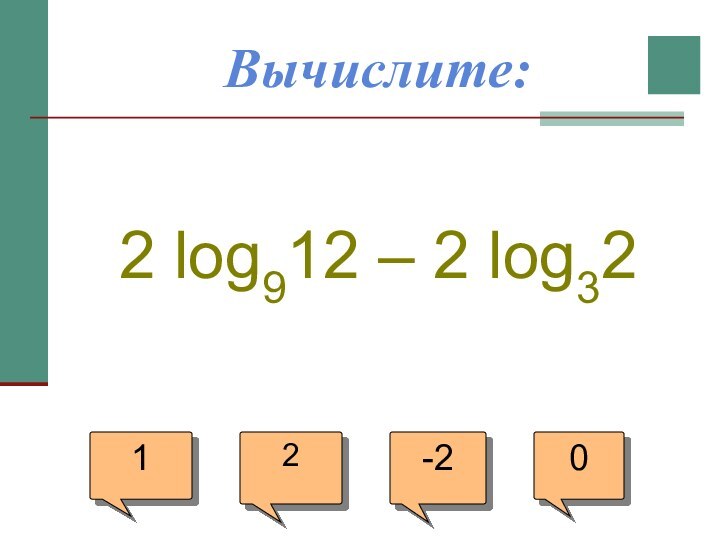Вычислите:5 log24 ∙ log39 + 3log65 ∙ 2log6525201510 Спасибо за урок log a b =α, Вычислите:2 log912 – 2 log3212-20 Решение:25-x2>0;X2-25 РешениеLog2(x2-1) = log2(3x(x-1));О. Д. З: x2 -1>0, x1,3x(x-1)>0,x1X ≠ ±1, x≠ 0.X2-1
Слайды презентации

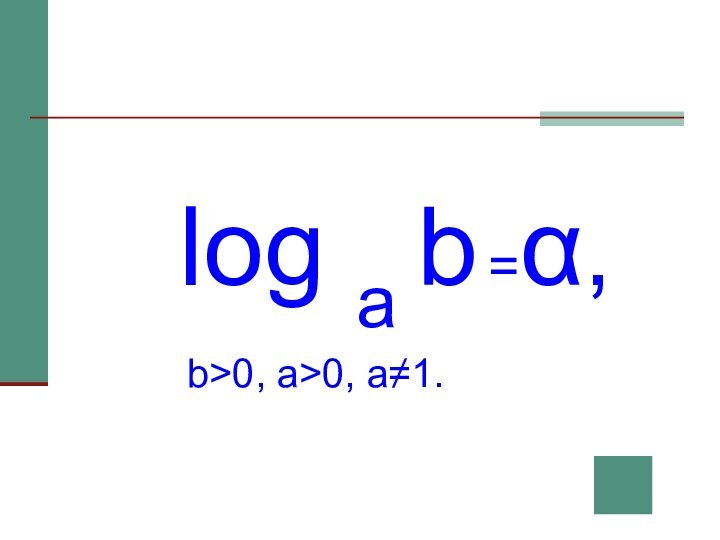
Слайд 2 Цели урока:


«Обобщить и закрепить понятие логарифмической функции, её

Цели урока:«Обобщить и закрепить понятие логарифмической функции, её свойства; свойства

свойства;
свойства логарифма; закрепить умения применять эти

понятия при решении уравнений, неравенств в целях подготовки к ЕГЭ ».

Слайд 3 Свойства логарифмов
Логарифмическая функция её свойства и график.
Графический диктант.
Определение

Свойства логарифмовЛогарифмическая функция её свойства и график.Графический диктант.Определение логарифмаЛогарифмические уравнения.Логарифмические неравенства.

логарифма
Логарифмические уравнения.
Логарифмические неравенства.

Слайд 4 Свойства логарифмов
Логарифм единицы.
Логарифм самого основания.
Логарифм произведения.
Логарифм частного.
Логарифм степени.

Свойства логарифмовЛогарифм единицы.Логарифм самого основания.Логарифм произведения.Логарифм частного.Логарифм степени.

Слайд 5 Задания на применение свойств логарифмов .
Найдите х:

Задания на применение свойств логарифмов . Найдите х: lg x=lg 3+2lg

lg x=lg 3+2lg 5 –lg 15.
Найдите х:

log3x=-1.
Найдите х: log0,5x=1.
Найдите х: logx81=4.
Вычислите : 7log72.
Вычислите: lg8+lg125.
Вычислите: lg130-lg13.

Слайд 6 Определение логарифма
1.Найдите выражения, имеющие смысл :
Log35, log50,

Определение логарифма 1.Найдите выражения, имеющие смысл :Log35, log50, log2(-4), log51, log55

log2(-4), log51, log55 .
2.Найдите верные равенства:
log28=3, log24= -2,

log24=2, log2(-16)=2.
3.Чему равны : lg100 и lg 0,001

Слайд 7 Графический диктант
1.Логарифмическая функция y=log a x определена

Графический диктант 1.Логарифмическая функция y=log a x определена при любом x.

при любом x.
2.Областью значений логарифмической функции является

множество действительных чисел.
3Областью определения логарифмической функции является множество действительных чисел.
4.Логарифмическая функция не является ни чётной , не нечётной.
5.Логарифмическая функция – нечётная.
6.Функция y=log3x – возрастающая.
7.Функция y=log a x при 0 8.График функции y=log a x пересекается с осью Ох.
9.График логарифмической функции находится в верхней полуплоскости.
10.График логарифмической функции всегда находится в l и 4 четвертях.
11.График логарифмической функции не всегда проходит через точку (1;0).
12.Не существует логарифм отрицательного числа.
13.Существует логарифм дробного отрицательного числа.
14.График логарифмической функции находится справа от оси оY.

Слайд 8 Ответы:

^-^-^-^-^-^-^-



14 правильных ответов – «5»
10-14 правильных

Ответы:^-^-^-^-^-^-^-14 правильных ответов – «5»10-14 правильных ответов – «4»7-9

ответов – «4»
7-9 правильных ответов – «3»
до

7 правильных ответов – «2»

Слайд 9 Возрастающая функция
Y=log a x , x>0.
При а>1 –

Возрастающая функцияY=log a x , x>0.При а>1 – функция возрастающая.Log 2 x < 2;Log 2x

функция возрастающая.

Log 2 x < 2;
Log 2x

меняется !


y

x

0

1

Y=log2x

Слайд 10 Убывающая функция
Y=log a x ,x>0,
При 0

Убывающая функцияY=log a x ,x>0,При 0

убывающая.
Log0,5x< -2;
Log0,5x4.
Знак меняется !
y
x
Y=log0,5x
0
1

Слайд 11 Логарифмические уравнения.
Log2(x+1) + log2(x+3) = 3;
О.Д.З:X>-1,X>-3;
Log2((x+1)(x+3)) = 3;
Log2((x+1)(x+3))

Логарифмические уравнения.Log2(x+1) + log2(x+3) = 3;О.Д.З:X>-1,X>-3;Log2((x+1)(x+3)) = 3;Log2((x+1)(x+3)) = log2 8;(x+1)(x+3)

= log2 8;
(x+1)(x+3) = 8;
X2+4x+3 = 8;
X2+4x-5 =

0;
X1=1;x2=-5;
-5 – посторонний корень.

Слайд 12 Решение неравенств.
Log3(x+2)0: x>-2.
Log3(x+2)

Решение неравенств.Log3(x+2)0: x>-2.Log3(x+2)


Log0,2(2-x)>-1;
2-x>0;xlog0,25;
2-x


-2

25

-3

2

Слайд 13 Найдите значение выражения lg a, если lg a3=9
81
3
9
310

Найдите значение выражения lg a, если lg a3=98139310

Слайд 14 Неверное решение!
Подумайте ещё!

Неверное решение!Подумайте ещё!

Слайд 15 Вы
выполнили
задание верно!

Вы выполнили задание верно!

Слайд 16 Найдите область определения функции y=log0,5( 25-x2)
(-∞;-5]U[5;+∞)

Найдите область определения функции y=log0,5( 25-x2)(-∞;-5]U[5;+∞) (-5;5) [-5;5](-∞;-5)U(5;+∞)?

(-5;5)
[-5;5]
(-∞;-5)U(5;+∞)
?

Слайд 17 Найдите сумму корней уравнения
Log2 (x2 – 1)=log2(3x(x –

Найдите сумму корней уравненияLog2 (x2 – 1)=log2(3x(x – 1))11/2Нет корней3/2?

1))
1
1/2
Нет корней
3/2
?

Слайд 18 Вычислите:


5 log24 ∙ log39 + 3log65 ∙ 2log65
25
20
15
10

Вычислите:5 log24 ∙ log39 + 3log65 ∙ 2log6525201510

Слайд 19 Спасибо за урок

Спасибо за урок

Слайд 20

log a b =α, b>0, a>0, a≠1.

log a b =α,


b>0, a>0, a≠1.

Слайд 21 Вычислите:


2 log912 – 2 log32
1
2
-2
0

Вычислите:2 log912 – 2 log3212-20

Слайд 22 Решение:
25-x2>0;
X2-25

Решение:25-x2>0;X2-25

(-5; 5)

-5

5

+

-

+

  • Имя файла: logarifmicheskaya-funktsiya.pptx
  • Количество просмотров: 109
  • Количество скачиваний: 0
- Предыдущая Обязательное медицинское страхование
Следующая - Потребность человечества в питании

Похожие презентации

Нумерация чисел в пределах 1000 Нумерация чисел в пределах 1000 129
Презентация Нумерация чисел от 11 до 20 презентация к уроку по математике (1 класс) Презентация Нумерация чисел от 11 до 20 презентация к уроку по математике (1 класс) 212
Презентация по математике на тему Сравнение дробей Презентация по математике на тему Сравнение дробей 145
1 класс презентация к уроку по математике (1 класс) по теме 1 класс презентация к уроку по математике (1 класс) по теме 97
Районный семинар по теме Площадь Районный семинар по теме Площадь 126
Длина окружности 6 класс Длина окружности 6 класс 119
Самостоятельные и контрольные работы учебно-методический материал по математике (2 класс) Самостоятельные и контрольные работы учебно-методический материал по математике (2 класс) 102
urok no2 kuprin slon urok no2 kuprin slon 65
Презентация Площадь презентация к уроку по математике (4 класс) Презентация Площадь презентация к уроку по математике (4 класс) 100
ЦОР по математике, 1 класс, по теме: Величины. Решение задач. план-конспект урока по математике (1 класс) ЦОР по математике, 1 класс, по теме: Величины. Решение задач. план-конспект урока по математике (1 класс) 147
Подготовка к контрольной работе по алгебре Подготовка к контрольной работе по алгебре 100
Площади. Формула площади прямоугольника Площади. Формула площади прямоугольника 110
Презентация по математике план-конспект урока по математике (4 класс) по теме Презентация по математике план-конспект урока по математике (4 класс) по теме 132
Числовые промежутки Числовые промежутки 140
Презентация по математике на тему Решение уравнений и неравенств. Закрепление (5 класс) для детей с ТНР. Презентация по математике на тему Решение уравнений и неравенств. Закрепление (5 класс) для детей с ТНР. 103
Математические преобразования в МР-томографии Математические преобразования в МР-томографии 110
Урок математики и презентация по теме:Свойство противоположных сторон прямоугольника. план-конспект урока по математике (2 класс) Урок математики и презентация по теме:Свойство противоположных сторон прямоугольника. план-конспект урока по математике (2 класс) 158
Действия с десятичными дробями Действия с десятичными дробями 90
Теорема Виета Теорема Виета 134
Математика КВН 1 класс презентация к уроку по математике (1 класс) по теме Математика КВН 1 класс презентация к уроку по математике (1 класс) по теме 141
Алгебра модуля Алгебра модуля 108
Решение тригонометрических уравнений, содержащих радикалы Решение тригонометрических уравнений, содержащих радикалы 104
Деление вида а:а, а:1 Деление вида а:а, а:1 129
Автоматты басқарудың математикалық моделдері Автоматты басқарудың математикалық моделдері 109
конкурсная программа по математике презентация урока для интерактивной доски по математике (2 класс) конкурсная программа по математике презентация урока для интерактивной доски по математике (2 класс) 119
Прямоугольник 2 класс Прямоугольник 2 класс 124
презентация использование занимательного материала для развития логического мышления дошкольников презентация к уроку по математике (подготовительная группа) презентация использование занимательного материала для развития логического мышления дошкольников презентация к уроку по математике (подготовительная группа) 122
Раскрась флажки игра-тренажёр по математике 2 класс по теме Уравнение презентация к уроку по математике (2 класс) Раскрась флажки игра-тренажёр по математике 2 класс по теме Уравнение презентация к уроку по математике (2 класс) 42
Презентация Ребусы презентация к уроку по математике (3 класс) Презентация Ребусы презентация к уроку по математике (3 класс) 101
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ (11 КЛАСС) ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ (11 КЛАСС) 121