Презентация на тему Обратные тригонометрические функции

Содержание

4. Тестирование:
5. Проверь и оцени .1)Критерии отметки:8– «5»,7,6– «4»,5,4– «3»0,1,2,3- «2»№ ВопросаПравильный вариант ответа
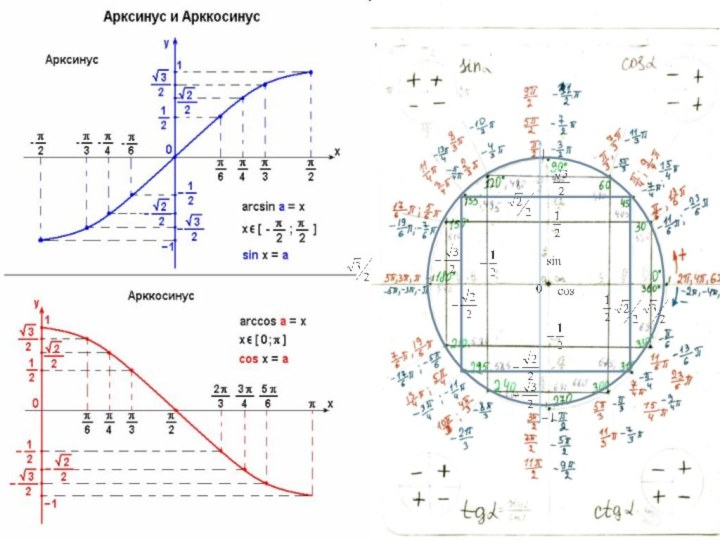
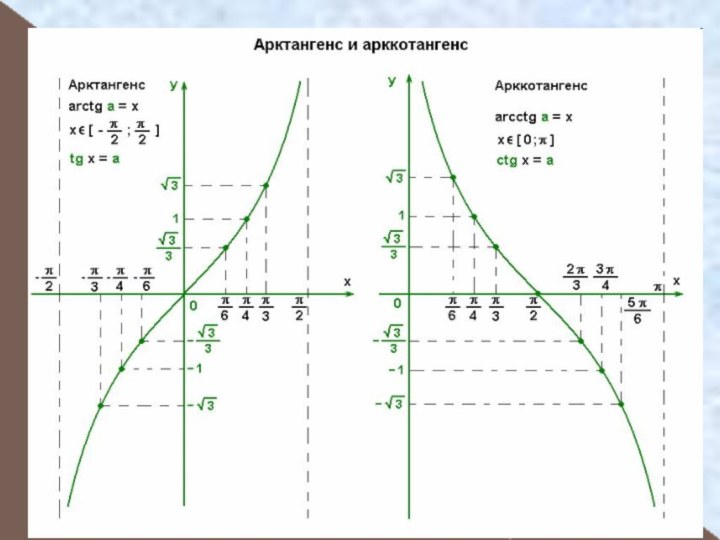
6. Свойства обратных тригонометрических функцийфункция arcsin m нечетная ,
7. Тригонометрические функции от одного и того же
8. Соотношения обратных
9. Доказать, что для всех x I
10. Решение упражнений и задач 1) Найдите значение
11. 3)Вычислите:аrcsin 0,15; arсcos 0,85; arctq(-0,65).
12. Практическая работаВычисление обратных тригонометрических функций с помощью программыMicrosoft Office Excel
13. Сегодня на уроке
15. Скачать презентацию
16. Похожие презентации

Тестирование:

Главная
Математика
Презентация Обратные тригонометрические функции

Тема урока:Math ZoneA = L x Wy= mx+ b3x+ 5 = 14A

Презентация Обратные тригонометрические функции

Проверь и оцени .1)Критерии отметки:8– «5»,7,6– «4»,5,4– «3»0,1,2,3- «2»№ ВопросаПравильный вариант ответа

Свойства обратных тригонометрических функцийфункция arcsin m нечетная , поэтому arcsin (-m) = -

Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна через

Соотношения обратных тригонометрических функций arcsin

Доказать, что для всех x I [-1; 1] верно arcsin x

Решение упражнений и задач 1) Найдите значение выражения:а) sin(arcsin 3/5); (устно!)

3)Вычислите:аrcsin 0,15; arсcos 0,85; arctq(-0,65).

Практическая работаВычисление обратных тригонометрических функций с помощью программыMicrosoft Office Excel

Сегодня на уроке я повторил….Мы узнали новые…..Занятие помогло

PS.Есть об алгебре молва Что она в порядок ум приводит. Потому хорошие

Слайды презентации

Слайд 4 Тестирование:

Слайд 5 Проверь и оцени .
1)
Критерии отметки:
8– «5»,
7,6– «4»,
5,4– «3»
0,1,2,3-

«2»

№ Вопроса
Правильный
вариант ответа

Слайд 6 Свойства обратных
тригонометрических функций
функция arcsin m нечетная , поэтому

arcsin (-m) = - arcsin m;
функция arccos m

ни четная, ни нечетная , поэтому arccos(−m)=∏ −arccosm;
функция arctg m нечетная, поэтому
arctg (-m) = - arctg m;
функция arcctg m ни четная, ни нечетная , поэтому arcctg(−m)=∏ −arcctgm

Слайд 7 Тригонометрические функции от одного и того же аргумента

Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна

выражаются алгебраически одна через другую, поэтому в результате выполнения

какой-либо тригонометрической операции над любой из аркфункций получается алгебраическое выражение.
В силу определения аркфункций:
sin(arcsin(x)) = x , cos(arccos(x)) = x,
(справедливо только для x є [-1;1] ).
tg(arctg(x)) = x ,
ctg(arcctg(x)) = x,
(справедливо при любых x ).

Слайд 8 Соотношения обратных тригонометрических функций arcsin m+arccos m=п/2, m

≤ 1 arctg m+arcctg m=п/2, mє R

Слайд 9
Доказать, что для всех x I [-1;

Доказать, что для всех x I [-1; 1] верно arcsin

1] верно
arcsin x + arccos x =

.
Доказательство:
arcsin x = – arccos x .
sin (arcsin x ) = sin ( – arccos x),
Воспользуемся формулой сложения для sin (a-b)=sin a cos b-cos a sin b:
sin( -arccos x)=1*cos(arccos x)- cos ( )*sin(arccos x)=

=cos(arccos x),
x = cos (arccos x ),
x = x.