на множители (выносим степень с наименьшим показателем)
Замена переменной, приведение
к квадратному (подстановка)Деление левой и правой частей уравнения на степень
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проект Уравнения и методы их решения
Содержание
- 2. Показательные уравненияОпред.: Уравнение вида aх=b , называется показательным
- 3. Методы решения:Приведение к одному основаниюРазложение левой части
- 4. Приведение к одному основанию:
- 5. Разложение левой части уравнения на множители:3 х+1
- 6. Замена переменной, приведение к квадратному:9х – 4
- 7. Деление левой и правой частей уравнения на
- 8. Примеры для самопроверки:
- 9. Типовые задания ЕГЭ:1.Решить уравнение:5х=125;2.Решить уравнение:
- 10. 4.Решить уравнение:3х+1 - 2 ·3х-2 =25;5.Решить уравнение:32х–
- 11. 8.Найти промежуток, которому принадлежат все решения уравнения:3
- 12. В4.Найти модуль разности корней:4х-√х²-5 - 12 ·
- 13. Тригонометрические уравнения
- 14. I) Уравнения Cosx=a, a [-1; 1]
- 15. Например. Cosx=, X=+ 2
- 16. II) Уравнения sinx=a, a 1; 1]
- 17. Например. Sinx=,(0; 1) X= (-1)narcsin+nZ X=
- 18. III) Уравнения tgx=a, a tgx=a, a0x=arctga + Ztgx= -a , ax= -arctga + n, nZ
- 19. Например. tgx=,[0;)x=arctg x=+Ztgx= -, -(-; 0) x= -arctg+n, nZx= - +Z
- 20. Методы решения тригонометрических уравнений.
- 21. 2.разложение левой части на множители Cosx=cos3xCosx-cos3x=0-2sin2xsin(-x) =0Sin2x=0
- 22. 3.однородное уравнение 1-ой степени asinx+bcosx=0 Решается делением
- 23. 4.однородное уравнение 2-ой степени asin2x+bsinxcosx+ccos2x=0 asin2x+bsinxcosx+ccos2x=0|:cos2x0atg2x+btgx+c=0tgx=t,
- 24. 5. Уравнение вида asinx+bcosx=c asinx+bcosx=cSinx +cosx=
- 25. Уравнения для самостоятельной работы! Базовый уровень Sinx=Cosx=-tgx=1+sin()=0Sin2x=Sinx+cosx=02cos(2x-)=Sin(x-)=0+1=0tgx-1=0
- 26. Повышенный уровень 2sin2x+3sinxcosx-2cos2x=0=03sinx+4cosx=10Sinx-sin2x+sin3x-sin4x=0Sinx-sin2x+sin3x-sin4x=0Cosx+cos=Sin3x-sin9x=0tg(3x+600)= ctg( -1)sin(-1)ctgx=04sincos=-Sinx-cosx=4sinxcos2x
- 27. Трудные задания Cos2x+cos22x+cos23x+cos24x=2(cos6x-1)ctg3x=sin3xCos(x+)+sin2x=-2Cos2x+|cosx|sinx=0Cos2x+sin22x+cos23x=(cos2x + 3 sinx-4)=0=0cosx+2sinx)=1-1=4sinx+ ctgxtg=0
- 28. Трудные заданияcosx-cos3x+2=0 удовлетворяющие условие: |x+|+2cosx=0=0,удовлетворяющие условию |x| –= -4+ =8
- 29. Уравнение с модулем Определение: a a
- 30. Методы решений. По определению модуля:|x+1|=3 =и = ==>x=-4
- 31. метод интервалов:|x+1| + |x-1| + |x+10|=121.найдём корни
- 32. метод интервалов:3.= = x=посторонний корень == =
- 33. метод интервалов: = ==x=– посторонний кореньОтвет:x1=-2 x2=0
- 34. Базовый уровень 1.|x+3|=122. x+5=|x|3. |x-15|=25x4.|2x|=1005.|x-40|=806.|x|=57. |x|=3x+108. |3x-9|=1
- 35. Повышенный уровень 1.| -
- 36. Логарифмические уравнения
- 37. При решение логарифмических уравнений применяют, такие преобразования,
- 38. логарифмическихМетодырешенияуравнений.
- 39. 1)Решение логарифмических уравнений на основании определения логарифма.(2x+1)=22x+1=2x+1=9X=4 (2×4+1)=Проверка9=2Ответ:х=4
- 40. 2)Метод приведения логарифмических уравнений к квадратному.(+1)=2ОДЗ: ==
- 41. 3) Метод потенцирования )ОДЗ = = =0Применяя метод потенцирования, получилиХ=6-+х-6=0=2, =-3 –п.кОтвет:х=2
- 42. 4)Метод приведения логарифмов к одному основанию. Используя
- 43. 5)Метод логарифмирования ОДЗ: = =x == 1+, 21+ 2X=3ОДЗ
- 44. Решить уравнение показательные по образцу.-6=4ОДЗ:== Ответ: Х
- 45. =6+2х-= Ответ:х=-1,х=21) =0 2) 3)
- 46. Решить логарифмические уравнения, упростив правую часть.1) 2) 3) 4)
- 47. Решить уравнение по образцу 2 Х=0∉ОДЗ , х=Ответ: х=
- 48. Решите уравнения, приведя к логарифмам с одинаковыми основаниями. lg (x+2) + 3+26)=03) +log3(-x-1)=02+x-5)+=log3-log4 =-9
- 49. Решить уравненияXlog3x-3=0,1x1+lgx=1Xlog4x=23(log4x+3)=0log3x-log3(x+8)=-log3(x+3)log2(x+1)+log2(x+2)=12log4(4-x)=4-log2(-2-x)log2(x+1)=1+2log2xlg(x+)-lg(x-)=lg(x+6)-lgxlog2 -1=log25x2-8x+5=0Log2 (24-x-2x+7)=3-x2log2(1-)=3log2(2+)+124log7(()0,75) = X2log2x+3 -6=0-4+log2(5-log0,2125)x2-x=0Log22Log2(log5x)=12+7=0Lg2(x+1)=lg(x+1)lg(x-1)+2lg2(x-1)3log2x2-log22(-x)=5logxlog25x=-1log3|x+8|+log3x4=2
- 50. Решить уравнениеLog3x+7(9+12x+4x2)+log2x+3(6x2+23x+21)=4log(100x3)lg=8log6(x+5)+log6x2=1=Log3(x+2)(5x)-log3Log4log2x+log2log4x=2-log77=4-log24=log77xlg+lglog23x+ log2x3+3log3x+3logx3=22log3xlog2x+2log3x-log2x-1=0
- 51. Метод монотонности функций.Теорема 1. Если одна из
- 52. Алгоритм решения уравнения методом использования монотонности.1.Иследовать на
- 53. , возрастает функция и -возрастающая и ()-возрастающая
- 54. Х=1 ,+ Х=4,--функция убывает, а-возрастает, теорему не
- 55. Уравнение с завуалированным обратным числом.()x +()x=8(4+)=16-16=1=4+=tt ()
- 56. Например! ()x + ()x=6( )x + ()x=10
- 57. Скачать презентацию
- 58. Похожие презентации
Показательные уравненияОпред.: Уравнение вида aх=b , называется показательным
![I) Уравнения Cosx=a, a [-1; 1] а) Cosx=a, а(0;](/img/tmb/6/597824/3a97935438c387ba35ca08879838483a-720x.jpg "Проект Уравнения и методы их решения")
![II) Уравнения sinx=a, a 1; 1] Sinx=a, a (0; 1)X= (-1)narcsina](/img/tmb/6/597824/eebce74fae4763fb173d2c48330c3f7e-720x.jpg "Проект Уравнения и методы их решения")
Слайд 3
Методы решения:
Приведение к одному основанию
Разложение левой части уравнения
на множители (выносим степень с наименьшим показателем)
к квадратному (подстановка)Деление левой и правой частей уравнения на степень
Слайд 4
Приведение к одному основанию:
2 3х · 3 х =576
(2³) х · 3 х =576
8 х ·3 х =576
24 х =24²=>х=2
Слайд 5
Разложение левой части уравнения на множители:
3 х+1 -
2 · 3 х-2 =25
3 х-2(3³-2)=25
3 х-2 · 25=25 |:25
3 х-2 = 1
3 х-2 = 30=>х-2=0
х=2
Слайд 6
Замена переменной, приведение к квадратному:
9х – 4 ·
3х – 45=0
32х– 4 ·3х -45=0
3х =t=>t²-4t-45=0
t1+t2 =4 t1 =9
t1 +t2 =45 t2 =-5п.к.
3х =9
3х =3²=>х=2
Слайд 7
Деление левой и правой частей уравнения на степень:
3х
= 52х
3х = 25 х |÷3х
1= 25 х 3
25 º 25 х =>x=0
3 3
Слайд 8
Примеры для самопроверки:
1
0,5х-1 9;
7 · 5х– 5х+1 = 2 · 5-3;27
2х² + 14 · 2х +1 – 29=0;
7х +6 · 3х +6=73х·33х
Слайд 9
Типовые задания ЕГЭ:
1.Решить уравнение:
5х=125;
2.Решить уравнение:
1
0,1х-1_ 16;32 ¯
3.Указать промежуток, которому принадлежит корень уравнения:
3х²+х-12 = 1;
Слайд 10
4.Решить уравнение:
3х+1 - 2 ·3х-2 =25;
5.Решить уравнение:
32х– 4
·3х– 45=0;
6.Решить уравнение:
32х-1 – 22х-1 = 0;
7.Решить уравнение:
32х+5– 22х+7
+ 32х+4 - 22х+4= 0;
Слайд 11
8.Найти промежуток, которому принадлежат все решения уравнения:
3 ·
16х + 2 · 81х =5 · 36х;
9.Указать промежуток,
которому принадлежит корень уравнения:52х– 4 · 5х– 5 = 0;
10.Решить уравнение:
3Sin²x + 3Cos²x = 4
Слайд 12
В4.Найти модуль разности корней:
4х-√х²-5 - 12 · 2х-1-√х²-5
+ 8 = 0;
В5.Решить уравнение:
23х-1 · 53х-1 = 100;
В6.Решить
уравнение:√3 · 2х − 4х − 2 = 1−2х;
В7.Решить уравнение:
32х+3 · 33х+1 · 625х+2 = 600х+7;
Слайд 14
I) Уравнения Cosx=a, a [-1; 1]
а) Cosx=a, а
(0; 1)
X=
аrccosa +2
n , n
б)Cosx=a, a
(-1;0)
X=
(
-arccosa) +2
Cosx=0
Cosx=-1
,
X=
+2
n
X=
+2
Cosx=1
X=2
Слайд 16
II) Уравнения sinx=a, a 1; 1]
Sinx=a, a
(0; 1)
X= (-1)narcsina +
n, n
Z
Sinx=a, a
(-1;0)
X= (-1)n+1arcsina+
n, n
Z
Sinx=
0X=
n, n
Z
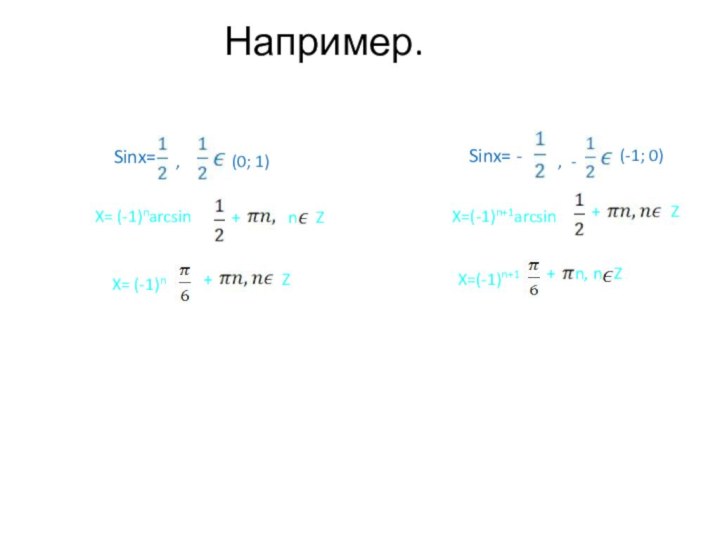
Sinx= 1
X=
+2
K, k
Z
Sinx= -1
X= -
+ 2
n, n
Слайд 17
Например.
Sinx=
,
(0; 1)
X= (-1)narcsin
+
n
Z
X= (-1)n
+
Z
Sinx=
-
, -
(-1; 0)
X=(-1)n+1arcsin
+
Z
X=(-1)n+1
+
n, n
Z
Слайд 20
Методы решения тригонометрических уравнений.
1)Уравнения, сводящиеся
к квадратным
а) Sin2x + sinx – 2=0
Sinx=t, t
[-1;1]
t2 +t-2=0
t1=1,
t2=-2-п.к так-1; 1]
как -2∉
sinx=1,
x=
+ 2
Слайд 21
2.разложение левой части на множители
Cosx=cos3x
Cosx-cos3x=0
-2sin2xsin(-x) =0
Sin2x=0
или
sinx=0
x=
2x=
X=
n
,
Слайд 22
3.однородное уравнение 1-ой степени asinx+bcosx=0
Решается делением на cosx0
0
+
= 0
sinx+cosx=0 |:cosx
atgx+b=0
x=-arctg
+
tgx+1=0
tgx=-1
+
x=-arctg1
n, n
Z
x=-
+
Слайд 23
4.однородное уравнение 2-ой степени asin2x+bsinxcosx+ccos2x=0
asin2x+bsinxcosx+ccos2x=0
|:cos2x
0
atg2x+btgx+c=0
tgx=t, at2+bt+c=0
Д=b2-4ac
t1,2=
tgx=
x1=arctg(
) +
n
x2= arctg(
) +
n
3sin2x-7sinxcosx+2cos2x=0|:cos2x
0
3tg2x-7tgx+2=0
tgx=t, 3t2-7t+2=0
Д= b2-4ac=25,
Дt1,2=
tgx=2
tgx=
x=arctg2+
x=arctg
+
k,
k
Z
Слайд 24
5. Уравнение вида asinx+bcosx=c
asinx+bcosx=c
Sinx +
cosx=
=cos
=sin
Cos
+ sin
cosx=
Sin (
+ x) =
X= (-1)narcsin
- +
z
n, n
Sinx-cosx=1
=
sinx –
cosx=
Sin( -
x
)=
X -
=
(-1)n
+
, n
Z
X= (-1)n
+
+
Слайд 25
Уравнения для самостоятельной работы!
Базовый уровень
Sinx=
Cosx=-
tgx=
1+sin(
)=0
Sin2x=
Sinx+cosx=0
2cos(2x-
)=
Sin(x-
)=0
+1=0
tgx-1=0
Слайд 26
Повышенный уровень
2sin2x+3sinxcosx-2cos2x=0
=0
3sinx+4cosx=10
Sinx-sin2x+sin3x-sin4x=0
Sinx-sin2x+sin3x-sin4x=0
Cosx+cos
=
Sin3x-sin9x=0
tg(3x+600)=
ctg(
-1)sin(
-1)ctgx=0
4sin
cos
=
-
Sinx-cosx=4sinxcos2x
Слайд 27
Трудные задания
Cos2x+cos22x+cos23x+cos24x=2
(cos6x-1)ctg3x=sin3x
Cos(x+
)+sin2x=-2
Cos2x+
|cosx|sinx=0
Cos2x+sin22x+cos23x=
(cos2x + 3
sinx-4)=0
=0
cosx+2sinx)=1
-1=4sinx
+
ctgxtg
=0
Слайд 28
Трудные задания
cosx-cos3x+2
=0
удовлетворяющие условие:
|x+
|
+2cosx=0
=0,
удовлетворяющие условию
|x|
–
= -4
+
=8
Слайд 31
метод интервалов:
|x+1| + |x-1| + |x+10|=12
1.найдём корни подмодульных
выражений:
X=-1 x=1
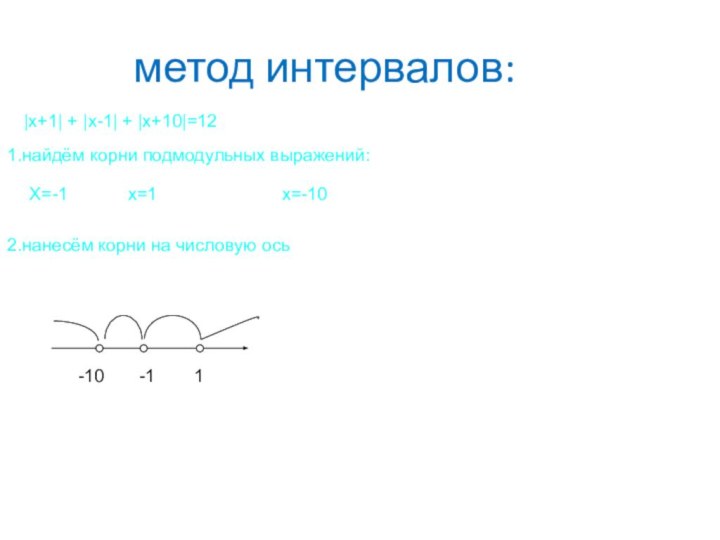
x=-102.нанесём корни на числовую ось
-10 -1 1
Слайд 34
Базовый уровень
1.|x+3|=12
2. x+5=|x|
3. |x-15|=25x
4.|2x|=100
5.|x-40|=80
6.|x|=5
7. |x|=3x+10
8. |3x-9|=1
Слайд 35
Повышенный уровень
1.|
-
– 5
=
2.|x2-5x+6|=x+1
3.|x-3|+2|x+1|=4
4.|5-2x|+|x+3|=2-3x
5.
=|x|+2
6. x|x|+7x+12=0
7.
x2-5x -
8. x2-|3x-5|=5|x|
9. |x+5|=|2x-3-x2|
10. 3|2x2+4x+1|=|x2+5x+1|
11.|2x-y-3|+|x+5y-7|=0
Слайд 37 При решение логарифмических уравнений применяют, такие преобразования, которые
не приводят к потери корней, но могут привести к
приобретению посторонних корней. Поэтому проверка каждого из полученных корней путем подстановок и их в исходное уравнение обязательно, если нет уверенности в равносильности уравнений. Проверку найденных корней можно заменить нахождением области определения уравнений. Тогда корнями уравнения, будут те числа, которые принадлежат этой области.
Слайд 39
1)Решение логарифмических уравнений
на основании определения логарифма.
(2x+1)=2
2x+1=
2x+1=9
X=4
(2×4+1)=
Проверка
9=2
Ответ:х=4
Слайд 40
2)Метод приведения логарифмических уравнений к квадратному.
(
+1)=2
ОДЗ:
=
=
X
По определению логарифма
(x+1
=2
+1
+2x+1=
+1
-2x=0
=0
=2
Ответ: х=2
Слайд 41
3) Метод потенцирования
)
ОДЗ
=
=
=
0
Применяя метод
потенцирования, получили
Х=6-
+х-6=0
=2,
=-3 –п.к
Ответ:х=2
Слайд 42 4)Метод приведения логарифмов к одному основанию. Используя формулу
=2n
f(x)
Где а
,а
1,n
z.
=2n|
|,
где a
,
a
.
ОДЗ:
-5
0 +5x-6=0
+
=-5
=-6
Слайд 44
Решить уравнение показательные по образцу.
-6
=4
ОДЗ:
=
=
Ответ: Х =1
)=
ОДЗ:
р.м.п
У=
У=0=
Д=4+24=28
=
х
1-
;
;
Слайд 48 Решите уравнения, приведя к логарифмам с одинаковыми
основаниями.
lg (x+2) +
3+26)=0
3) +log3(-x-1)=0
2+x-5)+
=log3
-log4
=-9
Слайд 49
Решить уравнения
Xlog3x-3=
0,1x1+lgx=1
Xlog4x=23(log4x+3)=0
log3x-log3(x+8)=-log3(x+3)
log2(x+1)+log2(x+2)=1
2log4(4-x)=4-log2(-2-x)
log2(x+1)=1+2log2x
lg(x+
)-lg(x-
)=
lg(x+6)-
lgx
log2
-1=log2
5x2-8x+5
=0
Log2 (24-x-2x+7)=3-x
2log2(1-
)=3log2(2+
)+12
4log7(
(
)0,75)
=
X2log2x+3
-6=0
-4+log2(5-log0,2125)x2-x=0
Log2
2
Log2(log5x)=1
2
+7=0
Lg2(x+1)=lg(x+1)lg(x-1)+2lg2(x-1)
3log2x2-log22(-x)=5
logx
log25x=-1
log3|x+8|+
log3x4=2
Слайд 50
Решить уравнение
Log3x+7(9+12x+4x2)+log2x+3(6x2+23x+21)=4
log(100x3)lg
=8
log6(x+5)+
log6x2=1
=
Log3(x+2)(5x)-log3
Log4log2x+log2log4x=2
-log77=
4
-log24=log77x
lg
+lg
log23x+ log2x3+3log3x+3logx3=2
2log3xlog2x+2log3x-log2x-1=0
Слайд 51
Метод монотонности функций.
Теорема 1. Если одна из функций
возрастает, а другая убывает
на промежутке, то уравнение f(x)=g(x)
имеет не более одного корня.Теорема 2. Если одна функция возрастает (убывает), а вторая принимает
постоянные значения на некотором промежутке, то уравнение
имеет не более одного корня.
Слайд 52
Алгоритм решения уравнения методом использования монотонности.
1.Иследовать на монотонность
функции f(x) и g(x) в О.О.У
2.Если выполняются условия теоремы
f(x) и g(x) и удается подобрать удовлетворяющие уравнению f(x)=g(x), то
-единственный корень
этого уравнения
, (
)-функция возрастает т.к
возрастает и
возрастает и в правой части уравнения постоянная функция, то
уравнения имеет один корень.
9+16=25
25=25
Слайд 53
,
возрастает функция и
-возрастающая и
(
)-возрастающая функция
,в правой части постоянная
функция.
Х=1, 6- 4
Х=2, 36-16
Х=3 ,
216-64=152
Слайд 54
Х=1 ,
+
Х=4,
-
-функция убывает, а
-возрастает, теорему не применять
Ф.М.У
а=
У=х-4,а=1 прямая направлена
Применяем теорему: уравнений имеет один
кореньХ=3 ,
-1=-1,
Х=3
Слайд 55
Уравнение с завуалированным обратным числом.
(
)x +(
)x=8
(4+
)=16-16=1=
4+
=t
t (
) =1=
4-
=
t+
=8|
t
t2-8t+1=0
д=b2-4ac=64-4=60
t1,2=
=
=4
(
)x=(4+
)
(
)x=(4-
)
=1
= -1
X=2 x= -2
