- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Орын ауыстыру және бөліктеп интегралдау тәсілдері
Содержание
- 2. Өткен тақырыптарға шолу Ауызша жаттығулар
- 5. Алғашқы функцияны табудың үш ережесі1 – ереже.
- 6. Алғашқы функцияны табудың үш ережесі2 – ереже.
- 7. Алғашқы функцияны табудың үш ережесі3 – ереже.
- 8. Анықталмаған интеграл кестесі
- 9. Ньютон-Лейбниц формуласыАнықталған интеграл
- 10. Есепте
- 11. Шешімі:
- 12. Есепте:
- 13. Шешімі:
- 14. Есепте:
- 15. Шешімі:
- 16. Мына функцияның графигі
- 17. Ответ:
- 18. Мына функцияның графигі
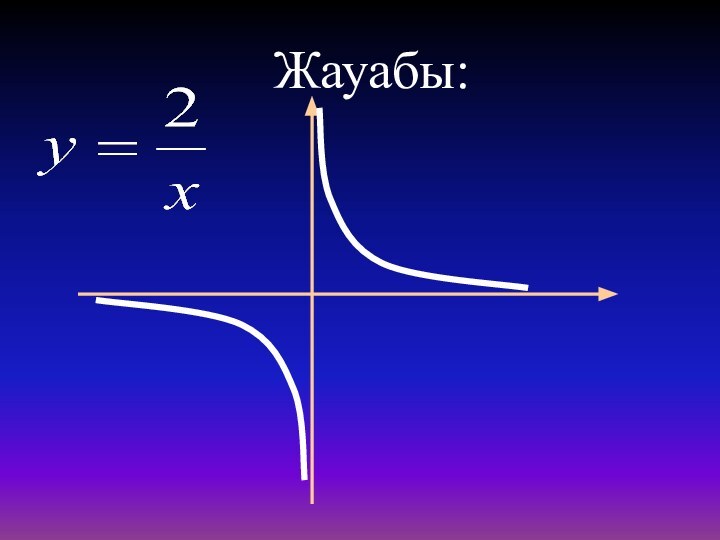
- 19. Жауабы:
- 20. Мына функцияның графигі
- 21. Жауабы:
- 22. Мына функцияның графигі
- 23. Жауабы:
- 24. Мына функцияның графигі
- 25. Жауабы:
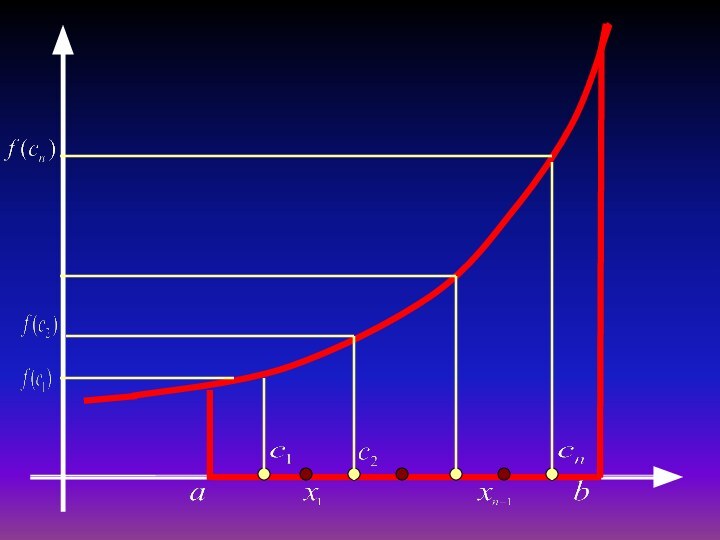
- 26. Қисық сызықты трапеция
- 27. y=f(x) функциясының графигімен және x=a, x=b түзулерімен,
- 28. Қисық сызықты тапеция
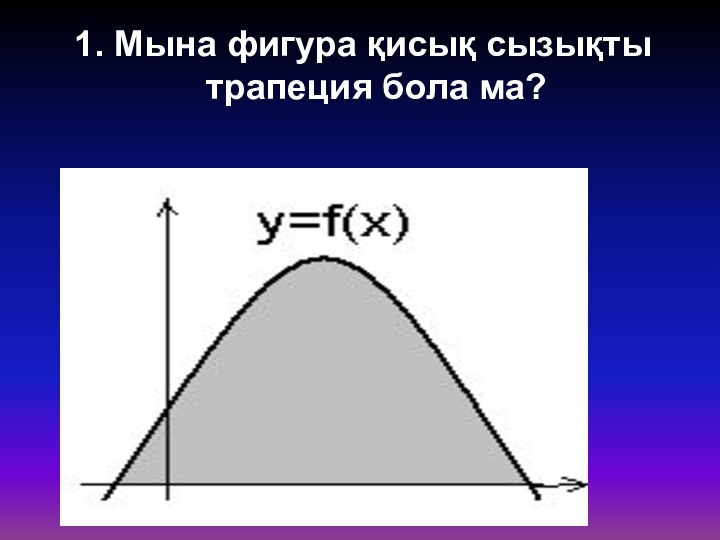
- 29. 1. Мына фигура қисық сызықты трапеция бола ма?
- 30. Жауабы: Ия
- 31. 2. Мына фигура қисық сызықты трапеция бола ма?
- 32. Жауабы: Ия
- 33. 3. Мына фигура қисық сызықты трапеция бола ма?
- 34. Жауабы: Ия
- 35. 4. Мына фигура қисық сызықты трапеция бола ма?
- 36. Жауабы: Ия
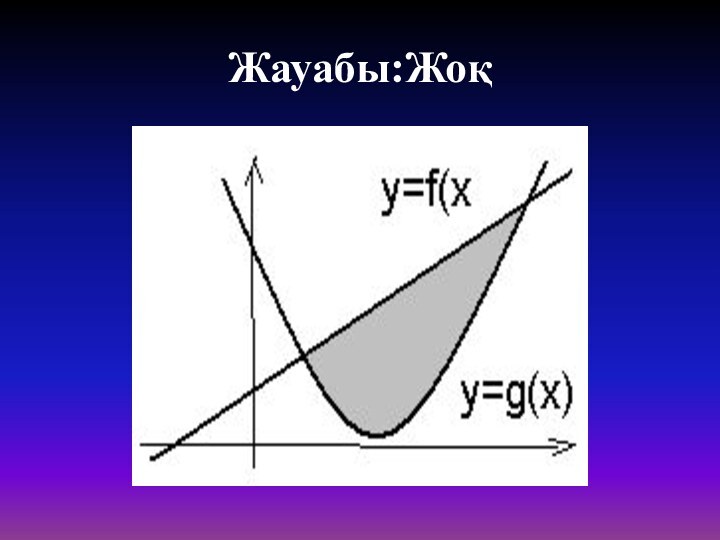
- 37. 5. Мына фигура қисық сызықты трапеция бола ма?
- 38. Жауабы:Жоқ
- 39. Қисық сызықты трапецияның ауданы
- 50. Жаңа тақырыпты түсіндіру
- 51. 1.Берілген интегралдың қай таблицалық интегралға келетіні анықтау2.Интеграл
- 52. 1-Мысал:
- 53. 2-Мысал
- 54. Бөліктеп интегралдау әдісіИнтеграл астында функциялардың көбейтіндісі, логарифмдік,
- 55. 3-Мысал:
- 56. 4-Мысал:
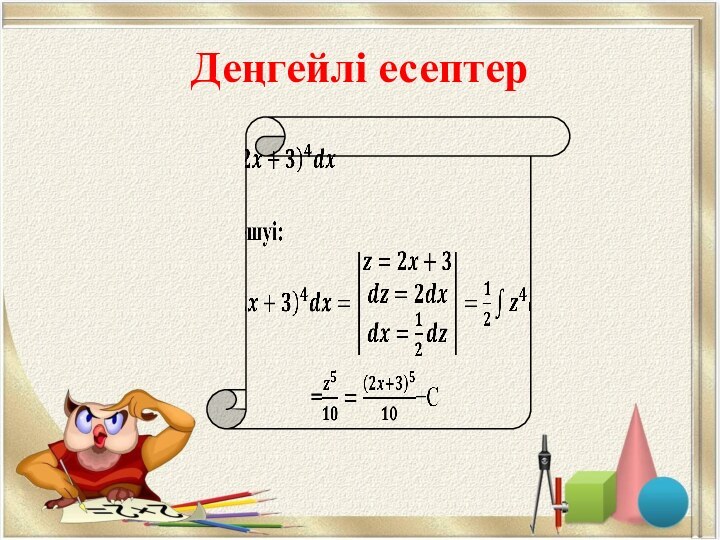
- 60. Деңгейлі есептер
- 61. Деңгейлі есептер
- 62. Деңгейлі есептер
- 63.
- 66. Скачать презентацию
- 67. Похожие презентации
Өткен тақырыптарға шолу Ауызша жаттығулар
Слайд 4 Алғашқы
функцияның негізгі қасиеті Белгілі бір аралықта ƒ(х)
функциясы үшін алғашқы функциялардың кез-келгенін мына түрде жазып көрсетуге болады, F (x) + С (1)
Слайд 5
Алғашқы функцияны табудың үш ережесі
1 – ереже.
Егер
ƒ үшін алғашқы функция F, ал g үшін алғашқы
функция G болса , ƒ + g үшін алғашқы функция F + G болады .
Слайд 6
Алғашқы функцияны табудың үш ережесі
2 – ереже.
Егер
ƒ үшін алғашқы функция F,
ал k – тұрақты
шама болса , онда kƒ үшін алғашқы функция k F болады .
Слайд 7
Алғашқы функцияны табудың үш ережесі
3 – ереже. Егер
F(x) функциясы ƒ (x) үшін алғашқы функция,
ал k
мен b – тұрақты шамалар болып , k ≠ 0 болса , онда ƒ (kx + b) функциясы үшін алғашқы функция ── F (kx + b) болады.
Слайд 27 y=f(x) функциясының графигімен және x=a, x=b түзулерімен, Ox
осімен шектелген фигура қисық сызықты трапеция деп аталады.
Слайд 51
1.Берілген интегралдың қай таблицалық интегралға келетіні анықтау
2.Интеграл астындағы
функцияның қай бөлігіне алмастыру енгізу керектігін анықтап, жазу
3.Алмастыру енгізілгеннен
кейін теңдіктің екі жағын да дифференциалдау4.Интеграл астына алмастыруды енгізу
5.Алынған интегралды табу
6.Шыққан нәтижеге алдыңғы алмастыруды қою.
Орын ауыстыру арқылы интегралдаудың ережелері:
Слайд 54
Бөліктеп интегралдау әдісі
Интеграл астында функциялардың көбейтіндісі, логарифмдік, кері
