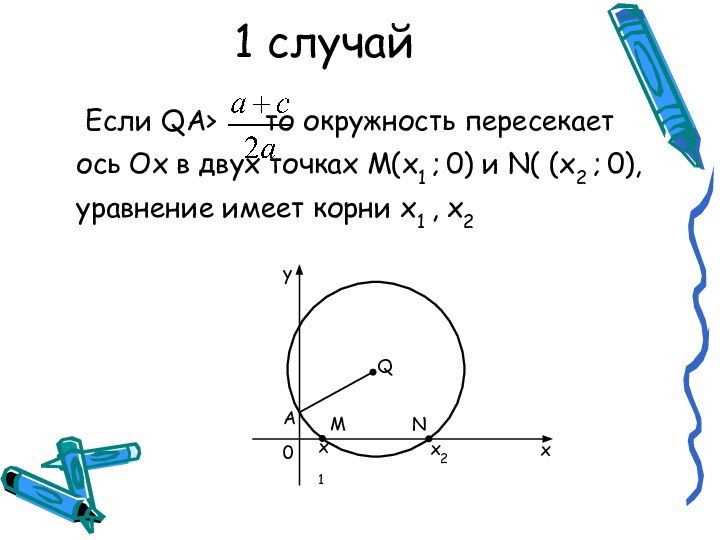
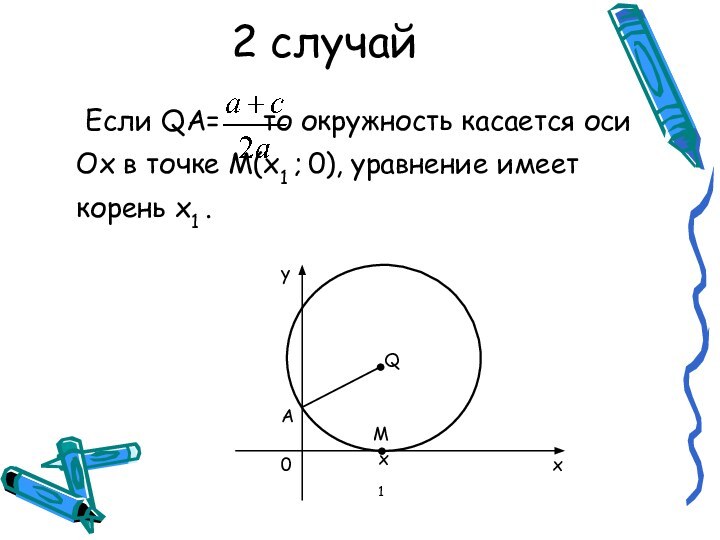
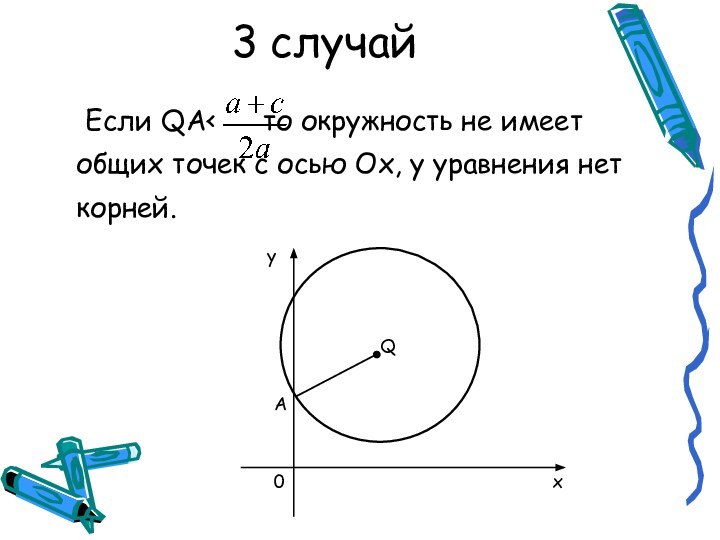
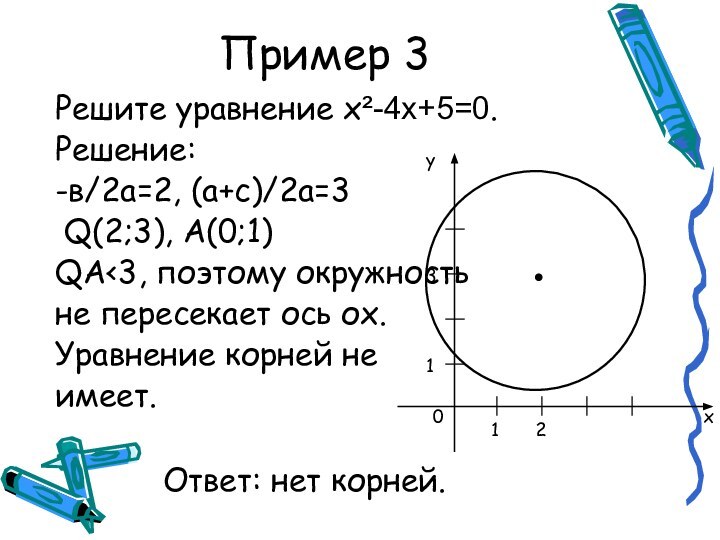
абсциссы точек пересечения окружности с центром
Q , проходящей через
точку А(0;1), и оси Ох.
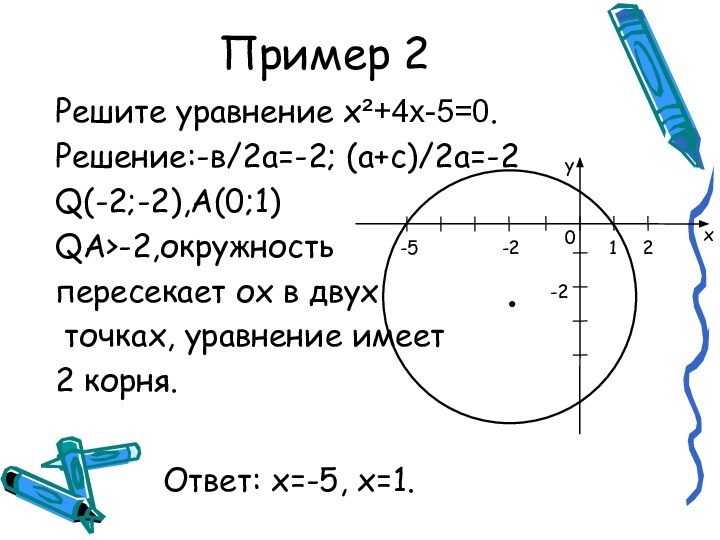
Решение уравнения сводится к построению на координатной плоскости окружности с центром Q и радиусом QA (для этого и понадобятся инструменты) и определению абсцисс точек пересечения окружности с осью Ох.
Возможны 3 случая: