- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Ортогональная проекция многоугольника и ее площадь
Содержание
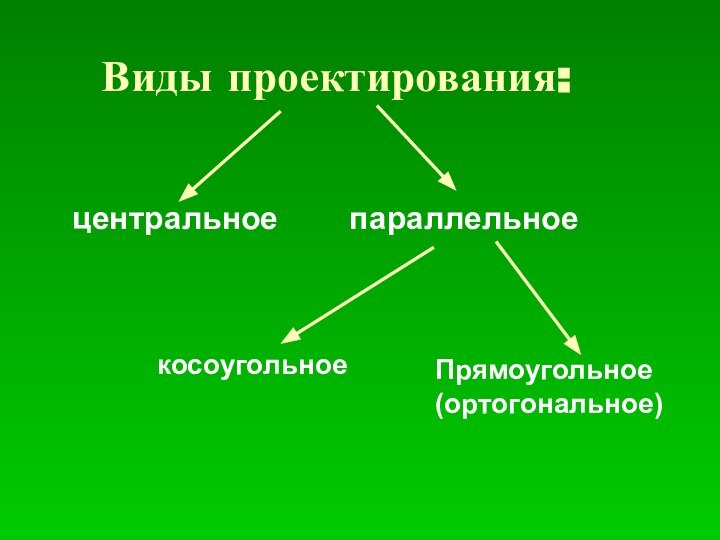
- 2. Виды проектирования:центральное параллельноеПрямоугольное(ортогональное)косоугольное
- 3. Свойства ортогонального проектированияПроекцией прямой является прямая.Проекцией параллельных
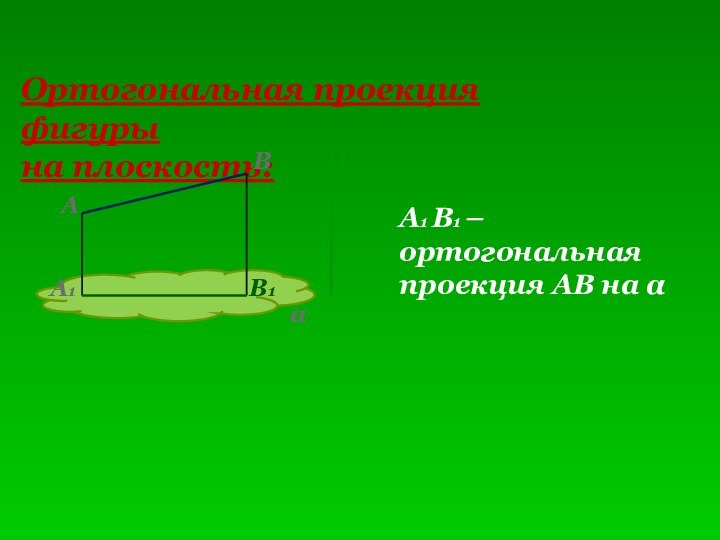
- 4. Ортогональная проекция фигуры на плоскость:lBAαB1A1A1 B1 – ортогональная проекция АВ на α
- 5. Ортогональная проекция фигуры на плоскость:lABCαA1B1C1Δ А1 В1 С1 – ортогональная проекция Δ АВС на плоскостьα
- 6. ΔАВС и ΔА1 В1 С1 могут быть
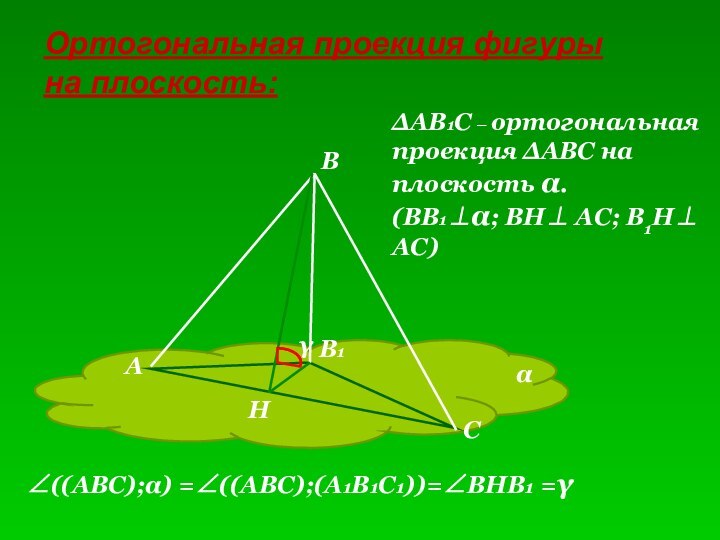
- 7. Ортогональная проекция фигуры на плоскость:ВАСВ1αНγΔАВ1С – ортогональная
- 8. S ΔAB1C =S ΔABC ⋅ cosγПлощадь ортогональной
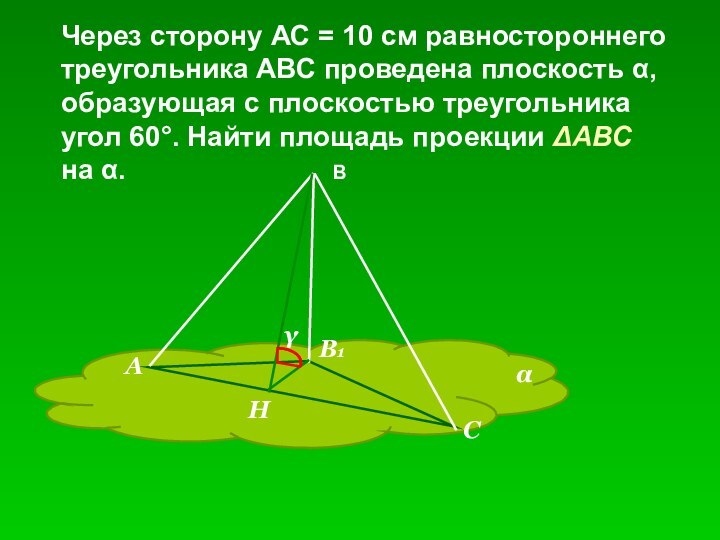
- 9. Через сторону АС = 10 см равностороннего
- 10. Ортогональной проекцией треугольника, площадь которого 420 является
- 14. Скачать презентацию
- 15. Похожие презентации
Виды проектирования:центральное параллельноеПрямоугольное(ортогональное)косоугольное






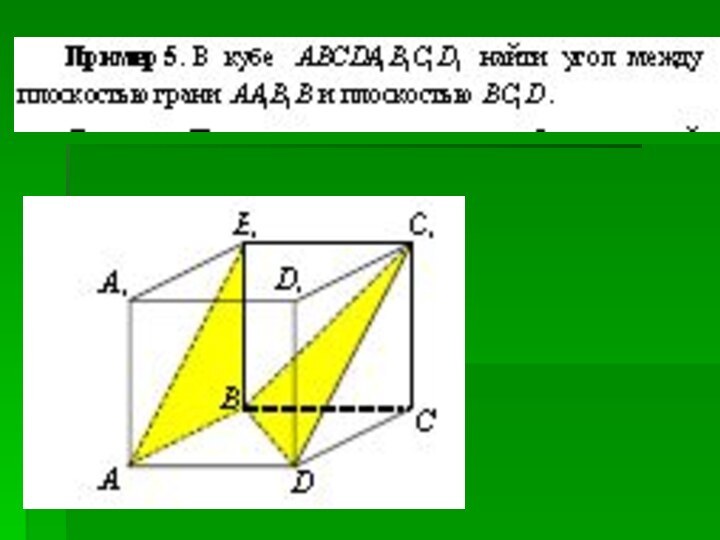
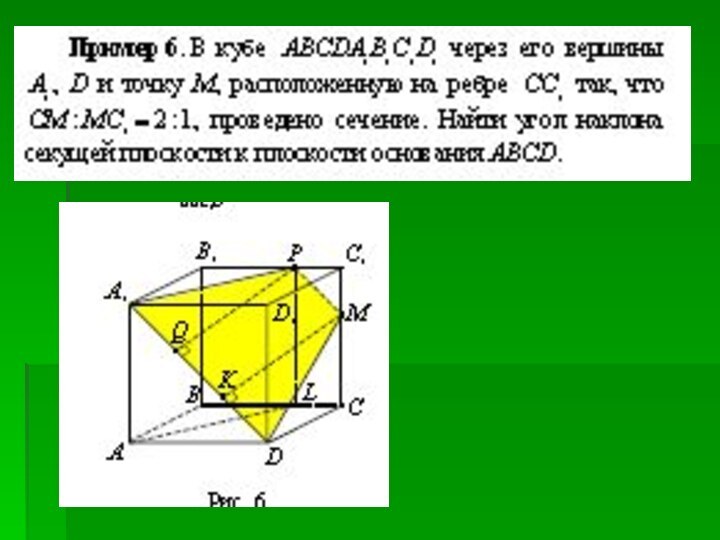
Слайд 3
Свойства ортогонального
проектирования
Проекцией прямой является прямая.
Проекцией параллельных прямых
являются параллельные прямые.
прямых.
Слайд 5
Ортогональная проекция фигуры
на плоскость:
l
A
B
C
α
A1
B1
C1
Δ А1 В1 С1
– ортогональная проекция Δ АВС на плоскостьα
Слайд 6
ΔАВС и ΔА1 В1 С1 могут быть равны,
а
могут быть и не равны.
РАВНЫ: если (АВС)⏐⏐ α.
НЕ
РАВНЫ: если угол между их плоскостями 0°< γ <90°.
Ортогональная проекция фигуры
на плоскость:
Слайд 7
Ортогональная проекция фигуры
на плоскость:
В
А
С
В1
α
Н
γ
ΔАВ1С – ортогональная
проекция
ΔАВС на
плоскость α.
(ВВ1⊥α; ВН⊥ АС; В1Н⊥ АС)
∠((АВС);α) =∠((АВС);(А1В1С1))=∠ВНВ1
=γ
Слайд 8
S ΔAB1C =S ΔABC ⋅ cosγ
Площадь ортогональной проекции
треугольника
равна произведению площади
треугольника на косинус угла между их
плоскостями.
Слайд 9
Через сторону АС = 10 см равностороннего
треугольника
АВС проведена плоскость α,
образующая с плоскостью треугольника
угол
60°. Найти площадь проекции ΔАВС на α.
А
С
В1
α
Н
γ
В