Слайд 2
Тақырыбы: Ең үлкен ортақ бөлгіш
Кіріспе: Ең үлкен ортақ
бөлгіштің шығу тарихы
Негігі бөлім:
Ең үлкен ортақ бөлгішті табудың тиімді
тәсілдері
Ең үлкен ортақ бөлгіш тақырыбына байланысты ашық сабақ
Қорытынды бөлім
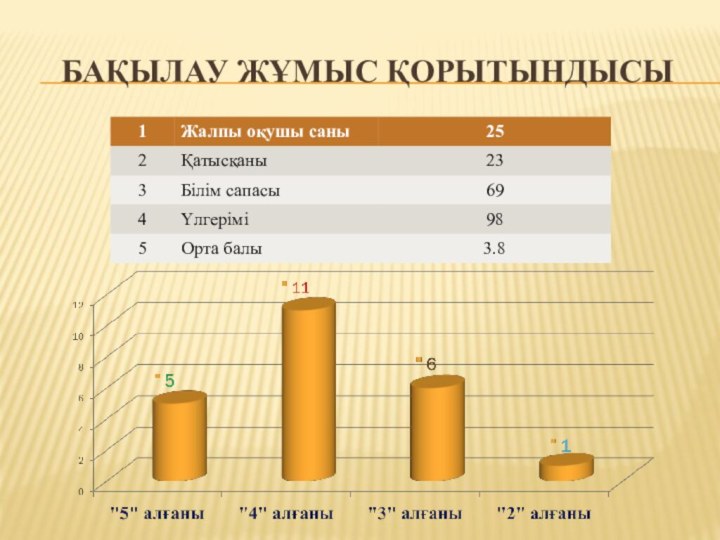
Бақылау жұмысы
Бақылау жұмысына сараптама
ҰБТ – те ЕҮОБ тақырыбына берілген есептерді шешу
Ең үлкен ортақ бөлгіштің шығу тарихы
Сандар теориясы — математиканың бүтін, рационал және алгебралық сандардың қасиеттерін зерттейтін саласы. Әсіресе оң натурал сандар 1, 2, 3, …, оның қасиеттері мен оларға арифметик амалдар қолдану сандар теориясының зерттеу аясында ерекше орын алады. Грекияда б.з.б. 6 ғ-да (Пифагор мектебінде) бүтін сандардың бөлінгіштігі зерттеліп, бүтін сандардың жеке түрлері (мыс., жай сандар, құрама сандар, квадрат сандар) ажыратылды, кемел сандардың құрылымы қарастырылды. Евклид “Негіздерінде” Евклид алгоритміне сүйеніп, екі бүтін санның ең үлкен ортақ бөлгішін табуға арналған жүйелі бөлінгіштік теориясы құрылды. Онда Евклид жай сандардың шексіз көп болатынын дәлелдеді.
Слайд 4
Негізгі бөлім
Ең үлкен ортақ бөлгішті табудың тиімді тәсілдері.

Екі не бірнеше натурал санның –
берілген сандардың әрқайсысы бөлінетін үлкен сан. Мысалы, 27 және 63 сандарының Ең үлкен ортақ бөлгіші 9 болса, 12, 32 және 60 сандарының Ең үлкен ортақ бөлгіші 4 болады. Ең үлкен ортақ бөлгіш бөлшектерді қысқарту кезінде пайдаланылады. Бұл ретте бөлшектің алымы да, бөлімі де қысқаратын ең үлкен сан Ең үлкен ортақ бөлгіш болып саналады. Егер берілген сандардың жай көбейткіштерге жіктелуі белгілі болса, онда ол сандардың Ең үлкен ортақ бөлгішін табу үшін, барлық жіктелуде кездесетін әрбір көбейткішті ең кіші рет алып көбейту керек. Жалпы жағдайда, екі санның Ең үлкен ортақ бөлгішін табу үшін Евклид алгоритмі пайдаланылады. Егер екі санның Ең үлкен ортақ бөлгіші бірге тең болса, онда ол сандар өзара жай сандар делінеді. а және b екі санның Ең үлкен ортақ бөлгіші (d) сол сандардың ең кіші ортақ еселігі m-мен мынадай қатынас арқылы байланысқан: dm=ab. Ең үлкен ортақ бөлгіш ұғымы сандарға ғана емес, екі не бірнеше көпмүшелікке де қолданылады. Бұл жағдайда екі не бірнеше көпмүшеліктің Ең үлкен ортақ бөлгіші, олардың әрқайсысы бөлінетін, дәрежесі ең жоғары көпмүшелік болады.
Слайд 5
m және n сандарының Ең үлкен ортақ бөлгіші
келесідегідей белгіленуі мүмкін:
•ЕҮОБ (m,n)
•
• (ағыл. Greatest
Common Divisor)
• (брит. ағыл. Highest Common Factor)
ЕҮОБ -ің табу жолы
18 санының бөлгіштері: 1, 2, 3, 6, 9, 18; 30 санының бөлгіштері:
1, 2, 3, 5, 6, 10, 15, 30.
Демек, 18 жөне 30 сандарының ең үлкен ортақ бөлгіші 6 саны. Жазылуы: ЕҮОБ(18, 30) = 6 Берілген натурал сандардың ең үлкен ортақ бөлгіші деп сол сандардың әрқайсысы бөлінетін ең үлкен натурал санды айтады.
Слайд 6
1-мысал. 8, 14 және 22 сандарының ең үлкен

ортақ бөлгішін табайық.
Шешуі.
8 санының бөлгіштері: 1, 2, 4, 8;
14 саныньщ бөлгіштері: 1, 2, 7, 14;
22 санының бөлгіштері: 1, 2, 11, 22.
8, 14 және 22 сандарының ортақ бөлгіштері: 1 және 2.
Ең үлкен ортақ бөлгіші - 2 саны. ЕҮОБ (8, 14, 22)=2.
2-мысал. 25 пен 12 сандарының ең үлкен ортақ белгішін табайық.
Шешуі. 25 санының бөлгіштері: 1, 5, 25.
12 санының бөлгіштері: 1, 2, 3, 4, 6, 12.
25 пен 12 сандарының ортақ бөлгіші бір ғана сан - 1 саны.
Ең үлкен ортақ бәлгіші 1-ге тең натурал сандар өзара жайсандар деп аталады.
Мысалы, 7 мен 11; 8 бен 15, 4 пен 19 сандары - өзара жай сандар.
3-мысал. 120, 40 жөне 20 сандарының ең үлкен ортақ бөлгішін табайық.
Шешуі. Берілген 120, 40 және 20 натурал сандарының ең кішісі 20 саны. 20 санына 120, 40 сандары бөлінеді. Сонда 20 саны - 120, 40 жөне 20 сандарының ең үлкен ортақ бөлгіші. ЕҮОБ (120, 40, 20)=20.
Егер берілген сандардың ең кішісі улкендерінің бөлгіші болса, онда сол ең кіші сан берілген сандардың ең үлкен ортақ бөлгіші болады.
Берілген сандардың ең үлкен ортақ бөлгішін сол сандарды жай көбейткіштерге жіктеу арқылы табуға болады. Ол үшін:
1 ) берілген сандарды жай көбейткіштерге жіктеу керек;
2) жіктеулердегі барлық ортақ жай көбейткіштерді табу керек;
3) ортақ жай көбейткіштердің көбейтіндісін табу керек.
Берілген сандардың ең үлкен ортақ бөлгіші сол сандардың жіктелуіндегі ортақ жай көбейткіштердің көбейтіндісіне тең.
4-мысал. 18, 66 жөне 330 сандарының ең үлкен ортақ бөлгішін берілген сандарды жай көбейткіштерге жіктеу арқылы табайық.
18 = 2 *3 * 3 66= 2*3*11 330 = 2*3*5 * 11
Берілген сандардың жіктелуіндегі ортақ жай көбейткіштер: 2 және 3 сандары, ал 2*3=6. Онда ЕҮОБ (18, 66, 330)=6
Слайд 7
Деңгейлеп оқыту
Деңгейлеп-саралап оқыту технологиясы 1998 оқу жылынан бастап мектептің
барлық сатысына, барлық пәндерге еніп, оқу үрдісін жандандыруға үлкен үлес қосып келеді.
Профессор Ж.Қараевтың деңгейлеп-саралап оқыту технологиясы жаңаша өзгерген мақсатпен оқушылардың өздігінен танып, іздену іс-әрекеттерін меңгертуді талап етеді. Бұл технологияда бірінші орында оқушы тұрады және өз бетімен білім алудағы белсенділігіне аса назар аударылды.
Әр оқушыға өз мүмкіндіктерін пайдалана отырып, білім алуына жағдай жасауға мүмкіндік береді.
Әр түрлі деңгейдегі балаларға саралай жұмыс істеуге мүмкіндік береді.
Онда білім игерудің 3 деңгейі қарастырылады: ең төменгі базалық деңгей, бағдарламалық, күрделенген деңгей, сондықтан әрбір оқушы оларды меңгеруі тиіс.
Слайд 8
Деңгейлеп оқыту
технологиясы нәтижелі болу үшін жеке тұлға ерекшеліктеріне, олардың психологиялық
даму ерекшеліктеріне, пән бойынша білімді меңгеру деңгейіне көңіл бөліп отырамын. Сабақты өткізу формаларын және түсіндіру әдістерінің жаңа тәсілдерін күнделікті сабаққа қолданамын. Көбінесе сабақтың мазмұнына, сабақ өткізудегі әдіс-тәсілдерді дұрыс таңдауға, сабақтың нәтижелігіне көңіл аударамын. Әр баланың мүмкіндік деңгейін ескере отырып логикалық есептерді шығаруға, нашар оқитын оқушылармен және дарынды балалармен де жұмыс жасаймын. Бұл әдіс арқылы әрбір оқушымен жеке жұмыс жүргізіп, әр оқушының интеллектуалдық даралығын анықтауға болады. Деңгейлеп оқыту арқылы оқушылардың сабаққа, білімге деген қызығушылығының артуы, ой жүйесінің дамуы, саналы білім алуы сияқты жетістіктерге жетуге болады деп ойлаймын. Осы мақсатпен 5-сыныпта «Ең кіші ортақ бөлгіш» тақырыбында деңгейлеп оқыту әдісін қолдану арқылы төмендегідей сабақ өткіздім.
Слайд 9
Менің педагогикалық мақсатым:
Оқудың мазмұнын және сапасын жетілдіру;
Әр күні

математика сабағында «Оқыту технологиясын» кең пайдалану;
Сынып ұжымы мен оқушының
шығармаларын арттыру мақсатында жұмыстану. І деңгейдегі оқушыларды ІІ деңгейге, ІІ деңгейдегі оқушыларды ІІІ деңгейге жеткізу.
Бұл әдістің тиімділігі:
-сыныптағы барлық оқушы бірдей жұмыс жасайды;
-бос отыратын оқушы болмайды;
-есеп шығарудың әр түрлі тәсілдерін меңгереді;
-әр түрлі деңгейдегі есептерді шығаруды үйренеді;
-сыныпты ұйымшылдыққа тәрбиелейді.
Деңгейлік тапсырмалар арқылы жеңілден қиынға, қарапайымнан күрделіге қарай сатылап оқушының ойлау қабілетін, білім сапасын сабаққа деген белсенділігін арттыруға болады. Сабақ барысында оқушы 2 аламын деп қорықпайды, керісінше тапсырманың жауабына жоғары ұпай жинау арқылы ынтасы артады. Сонымен бірге оқушы толық үлгеріп, өз бетімен жұмыс істеуге, тиянақты болуға талпынып, жауапкершілігі артады. Сондай-ақ жоғары деңгейдегі тапсырмаларды орындау арқылы дарынды оқушы таңдауға болады.
Слайд 10
І Сабақтың мақсаты:
а) білімділік:
Оқушыларға натурал сандардың
ең үлкен ортақ бөлгішін табуды үйрету және натурал сандардың ең үлкен ортақ бөлгішін табуға есептер шығарып жаттықтыру.
б) дамытушылық:
Оқушылардың логикалық ойлау қабілетін дамыту.
в) тәрбиелік:
Оқушыларды сабақта дұрыс отыруға, дәптерге таза жазуға үйрету. Этикалық және эстетикалық тәрбие беру.
ІІ Сабақтың түрі: аралас сабақ
ІІІ Сабақтың тәсілі: түсіндіру, сұрақ жауап
ІҮ Сабақ көрнекілігі: үлестірмелі қағаздар, интерактивті тақта
ҮІ Сабақтың барысы: а) ұйымдастырушы кезең: оқушыларды түгелдеп, үй жұмысын тексеріп, бағалау
б) Жаңа сабақ:
Слайд 12
Байыржан 5 дәптер мен 2 альбом үшін 130
теңге төледі.
Меруерт сондай 3 дәптер мен 2 альбом үшін
114 теңге төледі.
Дәптер мен альбом неше теңге тұрады?
дәптер – х
альбом – у
5х+2у=130
3х+2у=114 Бір-бірінен шегереміз. Сонда 2х=16, х=8
2у=130-5*8
2у=130-40
2у=90
у=45
жауабы: дәптер 8 теңге, ал альбом 45 теңге тұрады.
Слайд 13
Дүние жүзіндегі екінші ұстаз ,
қазақтың ежелгі ғалымы Әбу Насыр әл-Фараби Отырарда дүниеге келіп,
870-950 жылдар аралығында өмір сүрген. Неше жай сандар бар?
877,881,883,887,907,911,919,929,937,941,947 сонымен 11 жай сан бар екен.
Слайд 14
Амалды орындау:
5856:(61•16)-3060:(51•15)=(5856:61)•16-(3060:51)•15=
=96•16-60•15=1536-900=636
4374:(18•81)+3680:(23•32)=(4374:81)•18+(3680:32)•23=
=54•18+115•23=972+2645=3617
Слайд 15
23.11.2016 жыл
Ең үлкен ортақ бөлгіш
Слайд 16
32 және 24 сандарының барлық бөлгіштерін жазамыз:
32 :
1, 2 , 4 , 8 ,
16 , 32
24 : 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24
Ортақ бөлгіштері – 1, 2, 4 және 8 , олардың ең үлкені – 8
Слайд 17
Екі санның ең үлкен ортақ бөлгіші деп, берілген
сандардың әрқайсысы бөлінетін ең үлкен санды айтады
ЕҮОБ(32 ; 24
) = 8 деп жазамыз
Слайд 18
ЕҮОБ ( 630 ; 252 ) мәнін
табайық
630 2
315 3
105
3
35 5
7 7
1
252 2
126 2
63 3
21 3
7 7
1
ЕҮОБ ( 630 ; 252 ) = 2 * 3 * 3 * 7 = 126
Слайд 19
Cонымен екі санның ең үлкен ортақ бөлгішін табу
үшін:
Берілген сандарды жай көбейткіштерге жіктейміз ;
Шыққан жіктеудегі барлық
ортақ жай көбейткіштерді табамыз ;
Ортақ жай көбейткіштердің көбейтіндісін табамыз .
66 2 330
2
9 3 33 3 165 3
3 3 11 11 55 5
1 1 11 11
1
ЕҮОБ (18, 66, 330) = 6
2*3=6
Слайд 21
120, 40, 20
ЕҮОБ (120, 40, 20)=20
Егер сандардың ең
кішісі үлкендерінің бөлгіші болса, онда сол ең кіші сан
берілген сандардың ең үлкен ортақ бөлгіші болады.
Слайд 22
Ең үлкен ортақ бөлгіші 1 – ге тең
сандар өзара жай сандар деп аталады.
ЕҮОБ (10 ;21 )
= 1 ЕҮОБ ( 8 ; 9 ) = 1
= 2 * 5 8 = 8 * 1
21 = 3 * 7 9 = 9 * 1
Ауызша есепте
4 және 12
6 және 15
4 және 10
8 және 18
3 және 9
5 және 6
Слайд 24
Өзара жай сандарды табыңыз
Есептер шешу
Слайд 25
Ортақ бөлгішін және ең
үлкен ортақ бөлгішін табыңыз
Слайд 26
Логикалық есеп
42 дана қызыл шар, 54 дана көк
шар және 78 дана жасыл шарды әр түрлі түсті
шарлардың саны бірдей болатын етіп неше топқа жинау мүмкін?
42=2*3*7
54=2*3*3*3
78=2*3*13
ЕҮОБ(42; 54; 78)=2*3=6
Жауабы: 6 топқа жинауға болады.
Слайд 27
Есептер шешу №332
Х және Y сандарының ең үлкен
ортақ бөлгішін табыңыз
І деңгей
x=2*3*5 y=2*7*13
ЕҮОБ(2*3*5; y=2*7*13)=2
x=5*11*19 y=3*5*11
ЕҮОБ(5*11*19; 3*5*11)=5
ІІ деңгей
x=2*5*11*17 y=5*13*17*23
ЕҮОБ(3*5*11; 5*13*17*23)=5
2. x=2*11*19 y=5*7*13
ЕҮОБ(2*11*19; 5*7*13)=1
ІІІ деңгей
ЕҮОБ
ЕҮОБ
Слайд 28
№339
Ең үлкен ортақ
бөлгішін табыңыз
6; 8; 12
ЕҮОБ(6; 8;
12)=2
9; 27; 81
ЕҮОБ(9; 27; 81)=9
3) 8; 14; 18;
ЕҮОБ (8;
14; 18;)=2
І деңгей
42; 60; 84
ЕҮОБ(42; 60; 84)=6
45; 81; 99
ЕҮОБ(45; 81; 99)=9
3) 72; 78; 88;
ЕҮОБ (72; 78;88;)=2
ІІ деңгей
ІІ деңгей
231; 273; 399
ЕҮОБ(231; 273; 399)=21
253; 391; 207
ЕҮОБ(253; 391; 207)=23
3) 209; 437; 190;
ЕҮОБ (209; 437; 190;)=19
ІІІ деңгей
Слайд 29
Сабақты қорытындылау
60=2*2*3*5
450=2*3*3*5*5
ЕҮОБ(60;450) =2*3*5=30
Слайд 31
№343 ЕҮОБ(35,60)=5
ЕҮОБ (31,93) =31
ЕҮОБ (6,16) =2 ЕҮОБ (75,90)= 15
ЕҮОБ (54,66)=6 ЕҮОБ (50,200)= 50
ЕҮОБ (30,45) =15 ЕҮОБ(27,81) =27
ЕҮОБ(32,48)=16
ЕҮОБ (12,16)= 4 ЕҮОБ (36,90)= 18
ЕҮОБ(27,54,81)=27 ЕҮОБ(21,98) =7
ЕҮОБ (140,56)= 28 ЕҮОБ(18,120,138)=6
ЕҮОБ(42,56)=14 ЕҮОБ(110,154)=22
ЕҮОБ(11,22,44)=11
№344
ЕҮОБ(35,21,14)=7
Жауабы : 7тонна көмір әкелінді.
Слайд 32
ІІІ қорытынды бөлім
Бақылау жұмысы
Ең үлкен ортақ бөлгішті табыңдар
а)
ЕҮОБ(60;20), б) ЕҮОБ(1155;2015), в) ЕҮОБ(2158;2316);
2.
78 дана қызыл шар, 104 дана көк шар және 206 дана жасыл шарды әр түрлі түсті шарлардың саны бірдей болатын етіп неше топқа жинау мүмкін?
3. Берілген сандарды жай көбейткіштерге жіктеп, олардың ең үлкен ортақ бөлгішін тап
а) 48, 96, 108 б) 100, 210, 300 в) 1244, 1456
4. Темір жол стансасының жанынан белгілі бір уақыт аралығында үш пойыз өтті. Бірінші пойызда – 418, екіншісінде – 494, үшіншісінде – 456 жолаушы болды. Егер әр вагондағы жолаушылардың саны бірдей екені белгілі болса және олардың саны мүмкін болатын сандардың ең үлкенін алу керек болса, әр пойызда қанша жолаушы вагоны бар?
5. Теңдеуді шеш
56х-48х=1152
І нұсқа
Слайд 33
Ең үлкен ортақ бөлгішті табыңдар
а) ЕҮОБ(80;20), б)
ЕҮОБ(2155;3225), в) ЕҮОБ(2668;2816);
2. 98 дана қызыл
шар, 106 дана көк шар және 208 дана жасыл шарды әр түрлі түсті шарлардың саны бірдей болатын етіп неше топқа жинау мүмкін?
3. Берілген сандарды жай көбейткіштерге жіктеп, олардың ең үлкен ортақ бөлгішін тап
а) 58, 116, 136 б) 200, 310, 400 в) 1144, 1458
4. Темір жол стансасының жанынан белгілі бір уақыт аралығында үш пойыз өтті. Бірінші пойызда – 518, екіншісінде – 594, үшіншісінде – 556 жолаушы болды. Егер әр вагондағы жолаушылардың саны бірдей екені белгілі болса және олардың саны мүмкін болатын сандардың ең үлкенін алу керек болса, әр пойызда қанша жолаушы вагоны бар?
5. Теңдеуді шеш
35х-15х=400
ІІ нұсқа