- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Элементы теории множеств
Содержание
- 2. Множество есть многое, мыслимое нами как единое Георг Кантор(1845-1918)
- 3. МНОЖЕСТВА БЫВАЮТ КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕN – множество
- 4. Способы задания множеств:Перечислением элементовХарактеристическим условиемПорождающим правилом
- 5. АОбозначения множествВ настоящее время множества изображаются в
- 6. Множество, содержащее все множества и объекты рассматриваемой задачи, называется УНИВЕРСАЛЬНЫМ.U
- 7. Отношения между множествами
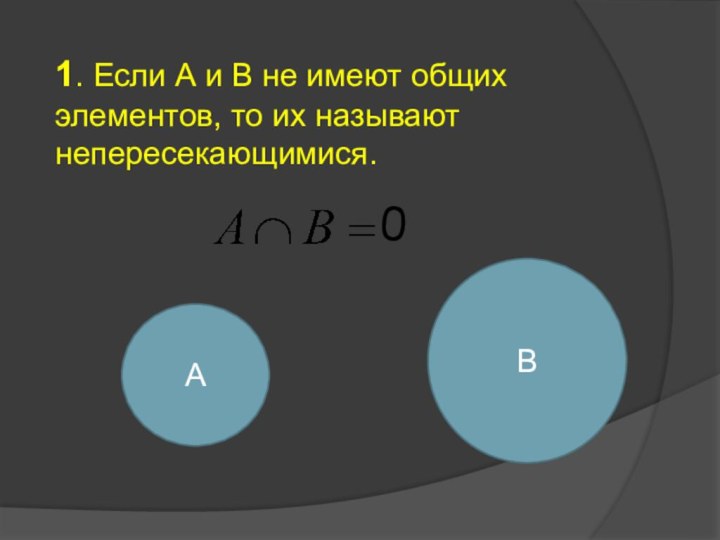
- 8. 1. Если А и В не имеют общих элементов, то их называют непересекающимися.01АВ
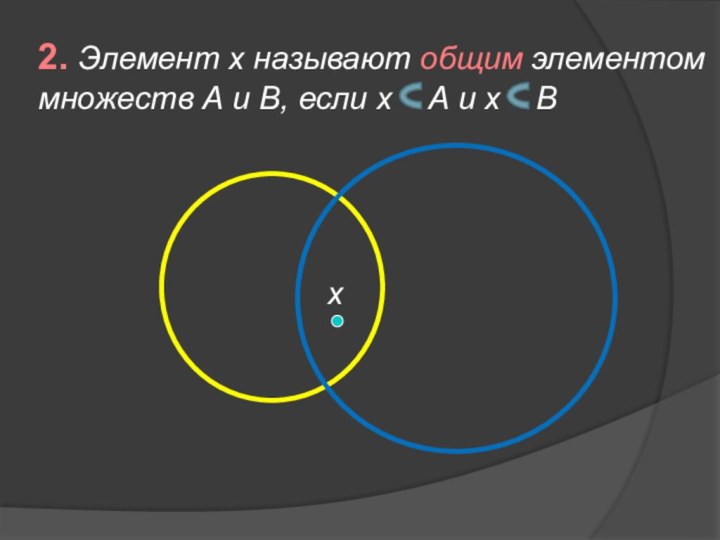
- 9. 2. Элемент х называют общим элементоммножеств А
- 10. 3. ПодмножествоВАВ - квадратыА - четырехугольникиМножество В
- 11. 4. Равные множестваЕсли множество В содержится в
- 12. Пустое множествоМножество называется пустым, если в
- 13. Скачать презентацию
- 14. Похожие презентации
Множество есть многое, мыслимое нами как единое Георг Кантор(1845-1918)








Слайд 3
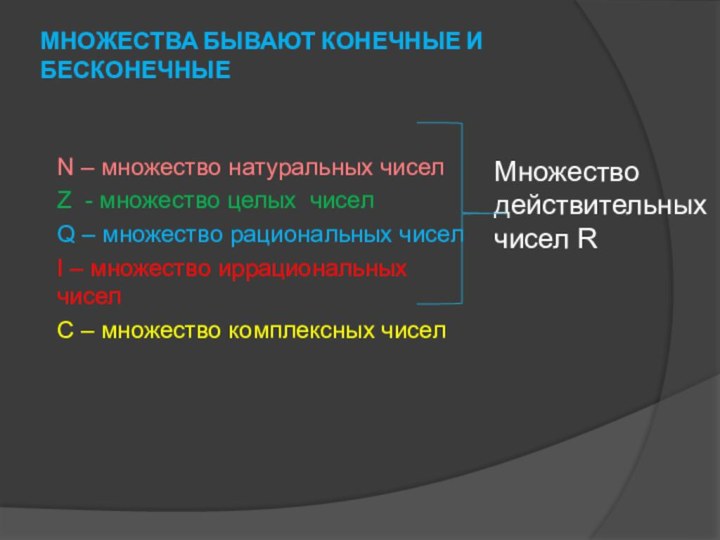
МНОЖЕСТВА БЫВАЮТ КОНЕЧНЫЕ И БЕСКОНЕЧНЫЕ
N – множество натуральных
чисел
Z - множество целых чисел
Q – множество рациональных чисел
I
– множество иррациональных чиселC – множество комплексных чисел
Множество действительных чисел R
Слайд 4
Способы задания множеств:
Перечислением элементов
Характеристическим условием
Порождающим правилом
Слайд 5
А
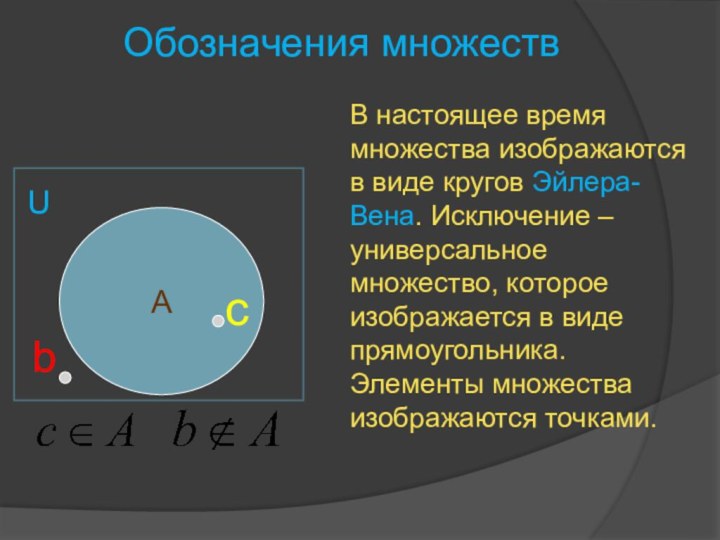
Обозначения множеств
В настоящее время множества изображаются в виде
кругов Эйлера-Вена. Исключение – универсальное множество, которое изображается в
виде прямоугольника. Элементы множества изображаются точками.с
b
U
Слайд 6
Множество, содержащее все
множества и объекты рассматриваемой
задачи,
называется
УНИВЕРСАЛЬНЫМ.
U
Слайд 10
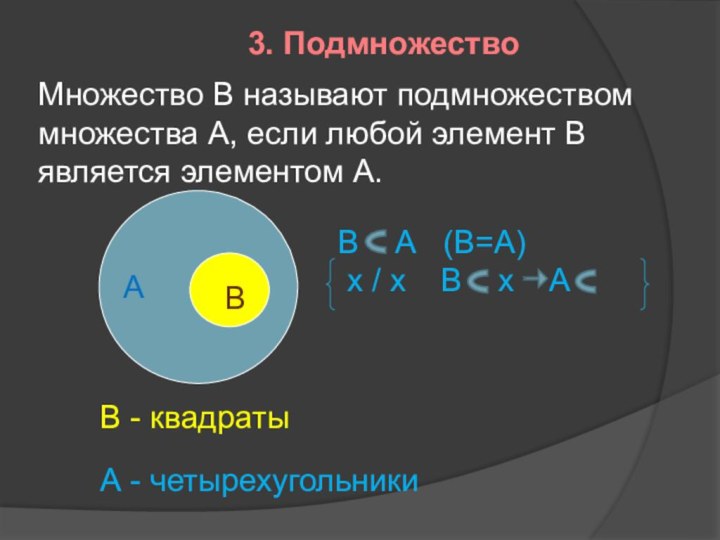
3. Подмножество
В
А
В - квадраты
А - четырехугольники
Множество В называют
подмножеством
множества А, если любой элемент В
является элементом А.
В А (В=А)
х / х В х А
Слайд 11
4. Равные множества
Если множество В
содержится в множестве
А, а множество А
содержится в множестве В, то А=В.
Если множество В содержится в множестве А и В не пустое, то оно называется собственным подмножеством множества А.
Слайд 12
Пустое множество
Множество называется пустым,
если в нем нет
ни одного элемента.
Считают, что является подмножеством
любого
множества и любое множествоявляется надмножеством самого себя.





























