- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логарифмы
Содержание
- 2. Открытие логарифмаОпределение логарифмаСвойства логарифмовДополнительные формулыСвойства логарифмической функцииГрафик
- 3. История логарифма началась в 17 веке. Логарифмы
- 4. Логарифмом числа b по основанию a называется
- 5. Свойства логарифмовПри любом a > 0 (a
- 6. loga b =logn b*logm c=logm b*logn clogak bk = loga b Дополнительные формулы
- 7. Логарифмическая функцияy = loga xD(y) = R+
- 8. a > 10 < a< 1
- 9. Решение логарифмических уравненийЛогарифмическое уравнениеУравнение, содержащее переменную под
- 10. Примеры решения уравненийxlog2x+2=8Прологарифмируем обе части уравнения по
- 11. Решение логарифмических неравенствЛогарифмическое неравенствоНеравенство, содержащее переменную только
- 12. Примеры решения неравенствlog5 (x - 3) <
- 13. Скачать презентацию
- 14. Похожие презентации









Слайд 2
Открытие логарифма
Определение логарифма
Свойства логарифмов
Дополнительные формулы
Свойства логарифмической функции
График функции
Решение
логарифмических уравнений
Слайд 3 История логарифма началась в 17 веке. Логарифмы были
изобретены шотландским дворянином Джоном Непером (1550-1617),опубликовавшим свои работы в
1614 году. Независимо от него и примерно в то же время пришел к открытию логарифмов швейцарский часовщик, математик и изобретатель Йост Бюрги (1552-1632), который опубликовал свои таблицы в 1620 году. Таблицы, опубликованные Непером и Бюрги были таблицами натуральных логарифмов, а первая таблица десятичных логарифмов опубликована в 1617 году Г.Бриггсом.открытие логарифма
Слайд 4 Логарифмом числа b по основанию a называется показатель
степени, в которую нужно возвести a, чтобы получить b(
loga b = c ac= b), при этом должно быть a > 0, a = 1, b >0Основное логарифмическое тождество: a loga b = b, b > 0
Слайд 5
Свойства логарифмов
При любом a > 0 (a =
1) и любых положительных x и y:
loga 1 =
0loga a = 1
loga xp = ploga x
loga xy = loga x + loga y
loga = loga x – loga y
loga x =
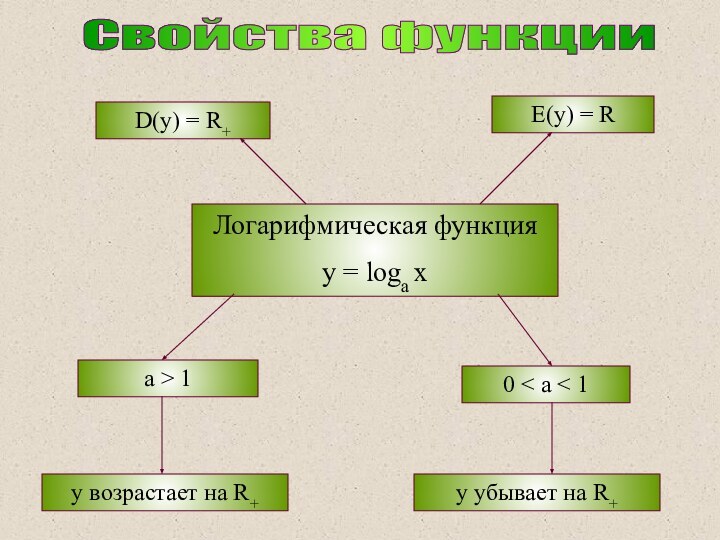
Слайд 7
Логарифмическая функция
y = loga x
D(y) = R+
E(y)
= R
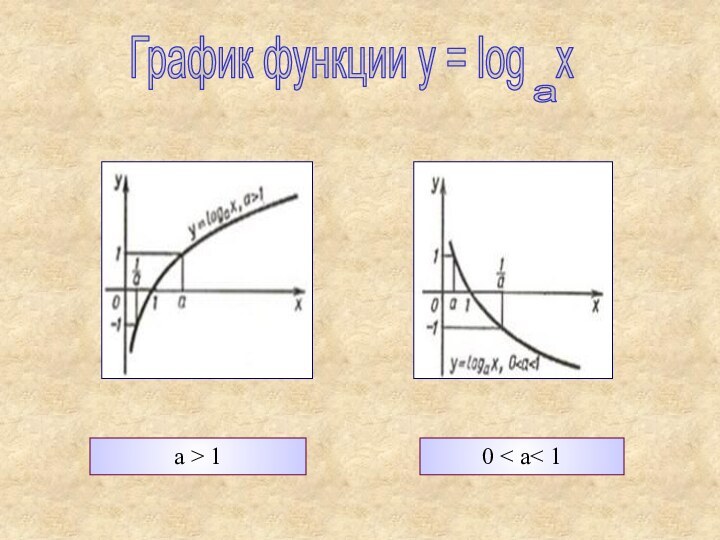
a > 1
0 < a < 1
y возрастает
на R+y убывает на R+
Свойства функции
Слайд 9
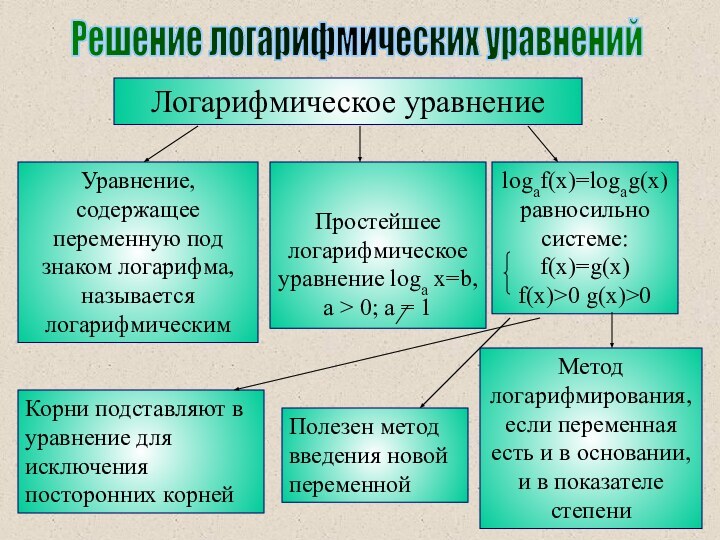
Решение логарифмических уравнений
Логарифмическое уравнение
Уравнение, содержащее переменную под знаком
логарифма, называется логарифмическим
Простейшее логарифмическое уравнение loga x=b, a >
0; a = 1logaf(x)=logag(x) равносильно системе: f(x)=g(x)
f(x)>0 g(x)>0
Корни подставляют в уравнение для исключения посторонних корней
Полезен метод введения новой переменной
Метод логарифмирования, если переменная есть и в основании, и в показателе степени
Слайд 10
Примеры решения уравнений
xlog2x+2=8
Прологарифмируем обе части уравнения по основанию
2:
log2(xlog2x+2)=log28,
(log2x+2)*log2x=3.
Пусть log2x=y, тогда
y2+ 2y - 3 = 0 ,
y
= 1 или y = -3.log2x=1 или log2x=-3
x = 2 или x = 1/8
log2(x-1)=6,
x-1>0, т.е. x>1
По определению логарифма:
x - 1 = 62
x – 1 = 36
x = 37
log52x - log5x = 2
Пусть log5x = y,
тогда y2 – y = 2,
y2 – y –2 = 0,
y = 2 или y = -1
log5x=2, log5x= -1
x = 25 или x = 1/5
Слайд 11
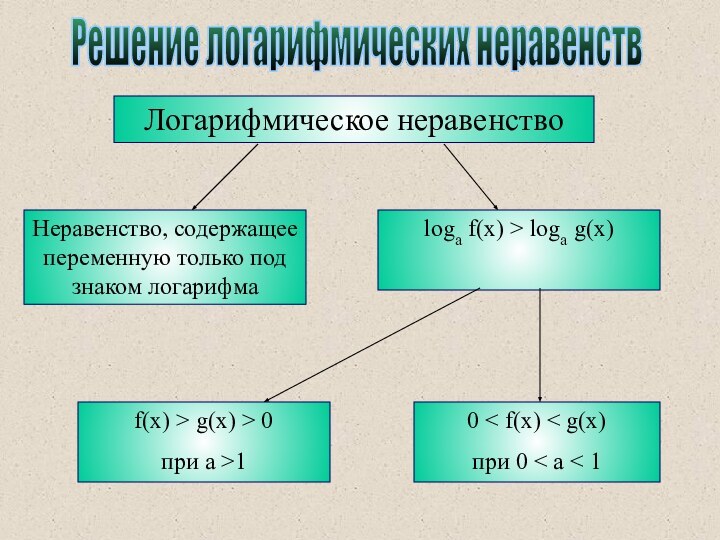
Решение логарифмических неравенств
Логарифмическое неравенство
Неравенство, содержащее переменную только под
знаком логарифма
loga f(x) > loga g(x)
f(x) > g(x) >
0при a >1
0 < f(x) < g(x)
при 0 < a < 1
Слайд 12
Примеры решения неравенств
log5 (x - 3) < 2
x
– 3 > 0
x – 3 < 25
x >
3x < 28
Ответ: (3;28)
log 0,5 (2x-4) > -1
2x – 4 > 0
2x – 4 < 2
x > 2
x < 3
Ответ: (2;3)