Слайд 2
Цель:
побудить и способствовать формированию различных активных видов
деятельности учащихся по подготовке к экзамену по математике.
Задачи
обучающая:
- формирование навыков решения заданий из открытого банка заданий ЕГЭ по математике
- расширение видов деятельности по подготовке к ЕГЭ и ГИА(в частности, изучению дополнительной литературы)
развивающая:
- способствовать развитию внимания
- формирование и постановка проблем в достижении целей учебной деятельности
- способствовать развитию логического мышления, математической интуиции, умению анализировать, применять знания
воспитательная:
- побудить у учащихся осознание системной подготовки к экзамену и ответственности за результаты экзамена.
Слайд 3
Принципы построения системы работы
Формирование основ знаний
Привлечение наглядных
средств
Обучение приемам самоконтроля
Отработка техники вычислений с целью повышения
общей культуры вычислений
Тренировка безошибочному преобразованию алгебраических вычислений и преобразований
Своевременное выявление в 7-9 классах детей с пробелами в математической подготовке и проведение коррекционной работы с ними
Подготовка к экзамену в течение всего периода обучения
Систематический контроль и диагностика результатов
Дифференцированный характер подготовки
Слайд 4
Формы организации работы учащихся при подготовке к итоговой
аттестации
использование медиапродукта на занятии
применение теста с просмотром решений
использование
для работы с электронным тестом в классе и бумажного вида работы
система работы в режиме онлайн
практикумы по темам повторения
зачеты по заданиям ЕГЭ и ГИА зачеты по заданиям ЕГЭ и ГИА Iзачеты по заданиям ЕГЭ и ГИА I части
знакомство и тренировка в решении экзаменационных задач в 6-8 классах
решение экзаменационных математических задач на уроках физики, химии (согласовано с учителями-предметниками)
система дополнительных занятий для детей, проявляющих интерес к математическим занятиям
Слайд 5
Целесообразность использования медиапродукта на занятии продиктована следующими факторами:
интенсификацией
учебно-воспитательного процесса:
автоматизацией процесса контроля,
улучшением наглядности изучаемого материала,
увеличением количества предлагаемой
информации,
уменьшением времени подачи материала;
повышением эффективности усвоения учебного материала за счет групповой и самостоятельной деятельности учащихся.
Слайд 6
Возможные варианты применения теста с просмотром решений
Используется учителем
для объяснения решений заданий В на уроках обобщающего повторения
или на факультативных занятиях по подготовке к ГИА и ЕГЭ.
Применяются для групповой работы с последующим обсуждением предложенных решений учителем и версий учащихся.
Применяются учащимися в качестве самопроверки полученного решения.
Используются для дистанционного обучения учащихся.
Слайд 7
Учащиеся в группах выполняют работу,
используя такие тесты, а проверка результатов проходит в электронном
тесте. Это занимает у учителя немного времени, но ожидание результатов работы группы активизирует деятельность учащихся на уроке, увлекает.
Слайд 8
Для работы с электронным тестом в классе использую
и бумажный вид работы. Для получения его, надо знать,
что такое СКРИНШОТ . СКРИНШОТ - это мгновенный снимок экрана монитора, изображение, которое показывает в точности то, что имеется на вашем мониторе.
Как его сделать?
Информация, которая находится на экране монитора, фотографируется кнопкой на клавиатуре Prt Sc SysRg. Затем зайти в Word, кнопкой Вставить . Получили СКРИНШОТ.
B
Слайд 9
режим онлайн
это не подготовленные заранее для егэ задания
по математике, это некое подобие примеров и задач, которые
могут быть на едином госэкзамене. А потому при подготовке к егэ по математике решения задач следует запомнить. Но лишь решения, а точнее ход их решений — это ведь не настоящий егэ по математике, ответы на который нужно занести в шпаргалки, а репетиция. Система в режиме онлайн конструирует каждый раз новые задачи, и совпадение их с теми, что будут на егэ в 2015 году, вряд ли возможно.
Войдя в систему, ученик может выбрать для подготовки к егэ по математике варианты: сложные и простые — все зависит от того, насколько усиленно он собирается готовиться и к каким результатам стремится. Что касается егэ по математике, баллы важно набрать высокие — ведь это один из обязательных школьных предметов.
Слайд 10
Тест по заданиям ЕГЭ
Например :
В задании
В4 предложено 455 прототипов. В данном тесте составлено 6
вариантов по теме «Треугольник». Использовались 240 прототипов из открытого банка заданий по математике по темам:
«Нахождение значений тригонометрических функций острых углов прямоугольного треугольника по одной из них»,
«Решение прямоугольных треугольников – нахождение сторон»,
«Теорема Пифагора»,
«Решение прямоугольных треугольников – нахождение углов»,
«Прямоугольный треугольник и высота, проведённая к гипотенузе»,
«Равнобедренный треугольник»,
«Равносторонний треугольник»,
«Тупоугольный треугольник»,
«Внешний угол треугольника – тригонометрия».
Слайд 11
Наглядная презентация изучаемого учебного материала
Структура презентации:
№ 1 Перечень

задач из открытого банка заданий, решаемых при помощи графика
линейной функции. Переход по гиперссылкам к условию и решению указанных задач
№ 2 Перечень задач из открытого банка заданий, решаемых при помощи графика квадратичной функции. Переход по гиперссылкам к условию и решению указанных задач
№3 - № 4 Завершающий слайд.
№ 5 Условие и решение задачи «Момент инерции вращающейся катушки» - задание B10 (№ 28165)
№ 6 - № 7 Условие и решение задачи «Торможение автомобиля» - задание B10 (№ 28147)
№ 8 - № 9 Условие и решение задачи «Мотоциклист в зоне сотовой связи» - задание B10 (№ 28135)
№ 10 - № 11 Условие и решение задачи «Время проверки работы лебёдки» - задание B10 (№ 28125)
№ 12 - № 13 Условие и решение задачи «Нагревание прибора» - задание B10 (№ 28115)
№ 14 - № 15 Условие и решение задачи «Камнеметательная машина» - задание B10 (№ 28105)
№ 16 – № 17 Условие и решение задачи «Полное вытекание воды из бака» - задание B10 (№ 28091)
№ 18 - № 19 Условие и решение задачи «Частичное вытекание воды из бака» - задание B10 (№ 28081)
№ 20 - № 21 Условие и решение задачи «Скорость вращения ведёрка» - задание B10 (№ 28071)
№ 22 - № 23 Условие и решение задачи «Мяч, подброшенный вверх» - задание B10 (№ 28059)
№ 24 Условие и решение задачи «Выручка предприятия при наибольшей цене» - задание B10 (№ 28053)
.№ 25 Условие и решение задачи «Мальчик, камешки, колодец» - задание B10 (№ 28039
)№ 26 - № 27 Условие и решение задачи «Месячная прибыль предприятия» - задание B10 (№ 28027)
№ 28 - № 29 Условие и решение задачи «Тепловое расширение рельса» - задание B10 (№ 28017)
Слайд 12
Возможные варианты применения иллюстрированных решений
Используется учителем для объяснения
решений данных заданий на уроках обобщающего повторения или на
факультативных занятиях по подготовке к экзамену.
Применяется учащимися в качестве самопроверки полученного решения.
Для дистанционного обучения учащихся.
Слайд 13
Обоснование выбора формы иллюстрирования решения

При подготовке к ЕГЭ по математике задания
В10 вызывают значительную сложность у выпускников. Это, прежде всего, продиктовано неумением учащихся «вчитываться» в текст задачи.
Поэтому в данной иллюстрации решений заданий В10 предлагается следующая схема:
анализ данных (данные),
функция,
график, соответствующий данной функции (построение, изображение на графике данных, соответствующих условию задачи),
решение соответствующего уравнения или неравенства,
обоснование и выбор ответа.
В зависимости от рассматриваемой задачи последовательность предлагаемых шагов может меняться.
Выбранная иллюстрация решений предполагает закрепление у учащихся базовых предметных знаний и умений:
умение графически решать уравнения,
умение графически решать неравенства,
знание и применение свойств квадратичной функции (направление ветвей параболы, нахождение точек пересечения с осями координат и др.)
знание и применение свойств линейной функции,
нахождение значения функции по графику,
нахождение длины отрезка.
дидактический материал для проведения зачета в 5 вариантах с
ответами
Тема – « Задания ЕГЭ I части (1 полугодие)»
Данный дидактический материал содержит по 5 заданий по 10 основным темам:
тема 1. «Степени»,
тема 2. «Корни n-ой степени»,
тема 3. «Область определения функции и множество значений функции»,
тема 4. «Производная и её применение»,
тема 5. «Решение уравнений»,
тема 6. «Решение неравенств» ,
тема 7. «Тригонометрия»,
тема 8. «Чтение графиков»,
тема 9. «Логарифмы»,
тема 10. «Первообразная и неопределенный интеграл ».
Слайд 22
Уравнения с одной переменной
Подготовка к экзамену
9 класс
Слайд 23
Уравнения с одной переменной
Определение
Равенство с переменной f(x)=g(x)
называется уравнением с одной переменной.
Корень уравнения
Значение переменной, при
котором уравнение обращается в верное равенство называется корнем уравнения
Слайд 24
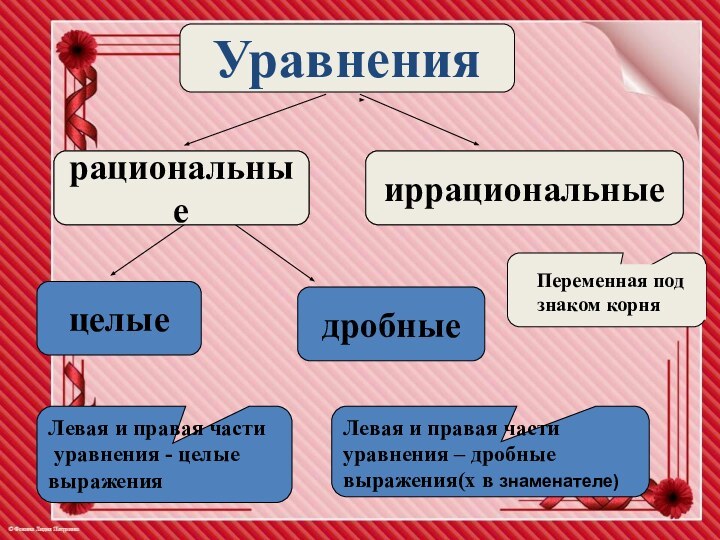
Уравнения
иррациональные
рациональные
целые
дробные
Левая и правая части
уравнения - целые
выражения
Левая
и правая части
уравнения – дробные
выражения(х в знаменателе)
иррациональные
рациональные
Переменная под
знаком
корня
Слайд 25
Целые уравнения
Линейные уравнения и уравнения, приводимые к виду
ax=b
5х=20 ; -3х+63=12 ; 3-5(х+1)=6-4х
; (х+1)/2+5х/12=3/4
Квадратные уравнения и уравнения, приводимые к виду ax2+bx+c=0
3x2+5x+2=0; 3x2 -12x=0; х(х+2)=3 ; x2 -6x=4х-25 ;
(3х+1)(6-4х)=0 .
Слайд 26
Квадратным уравнением называется уравнение вида
ax2+bx+c=0, где коэффициенты a, b, c – любые действительные
числа, причем а=0
Приведенное, если а=1 x2+3x- 4=0
Неприведенное, если а=1 2x2 -7x+5=0
Полное, если b и с отличны от нуля
Неполное , если b или с равны нулю
x2+4x=0 -5x2+45=0 4x2=0
Слайд 27
Решение неполных квадратных уравнений:
Слайд 28
Решение полных квадратных уравнений
x1=1, x2=c/a
x1=-1, x2=-c/a
Слайд 29
Решение дробных уравнений
Преобразовать уравнение к виду
Решить
уравнение p(x)=0
Найти область допустимых значений, т.е.
g(x)=0 (ОДЗ)
Проверить, удовлетворяют ли корни уравнения
p(x)=0 ОДЗ данного уравнения
Записать ответ
Слайд 30
Решение иррациональных уравнений
Возводим в квадрат левую и
правую части
уравнение
Решаем, получившееся рациональное
уравнение
Делаем проверку (при возведении в квадрат
могут появиться посторонние корни)
Слайд 31
1. 7x-0,5=6-1,5(2x+1)
Определите вид уравнения
2. 2x2+5x-3=0
3.
5. (x-1)(x+2)=0
4. 5x2+20x=0
6.
7.
8.
9.
10. 2x2-32=0
11.
(x-1)x=5(x-1)
Слайд 32
Ответы:
1. линейное:
1, 3
2. квадратное: - неполное 4, 10
- полное 2, 5, 11
3. дробное: 6, 8
4. иррациональное: 7, 9
Слайд 33
Решите самостоятельно уравнения
1. 7x-0,5=6-1,5(2x+1)
2. 2x2+5x-3=0
3.
5. (x-1)(x+2)=0
4. 5x2+20x=0
7.
8.
9.
10. 2x2-32=0
11.
(x-1)x=5(x-1)
6.
Слайд 34
Ответы и решения:
1.
7x-0,5=6-1,5(2x+1)
7x-0.5=6-3x-1.5
7x+3x=6-1.5+0.5
10x=5
X=5/10
X=0.5
3.
15
5(x-2)-30=3x
5x-10-30=3x
5x-3x=40
2x=40
X=20
Ответ: х=0,5
Ответ: х=20
Слайд 35
Ответы и решения:
4. 5x(x+4)=0
5x=0
x+4=0
x1=0 x2=-4
Ответ: -4; 0
10.
2x2=32
x2=16
x1=-4
x2=4
Ответ: -4; 4
2. 2x2+5x-3=0
x1=-3 x2=0,5
Ответ: -3; 0,5
5. (x-1)(x+2)=0
x-1=0 x+2=0
x1=1 x2=-2
Ответ: -2; 1
Слайд 36
Ответы и решения:
6.
(2-x)
2x-15=3x(2-x)
2x-15-6x+3x2=0
3x2-4x-15=0
ОДЗ: x=2
Ответ:
3
;
Слайд 37
Ответы и решения:
2x+1=9
2x=8
X=4
проверка:
Ответ: 4
7.
2x-5=4x+7
2x-4x=7+5
-2x=12
x=-6 проверка:
Ответ:
решений нет
9.
Слайд 38
Решим уравнения, используя методы:
разложения на множители;
введение новой переменной;
графический.
1
метод: разложение на множители.
Сборник заданий для подготовки к итоговой аттестации :
стр 102 №2.1(1); №2.3(1);
Стр 104 №2.22(1)
Слайд 39
Метод введения новой переменной
Уравнения вида aх4+bx2+c=0, где а=0,
является квадратным относительно х2, называют биквадратными уравнениями.
Х4-11х2-12=0
Пусть у=х2,тогда
у2-11у-12=0
у=-1
или у=12
Вернемся к переменной х
х2=-1 или х=12
решения нет
Х1.2=+-2 3
2. Сборник заданий для подготовки к итоговой аттестации
стр 104 №2.24(1), 2.25(1)
Сборник заданий для подготовки к итоговой аттестации
стр 102 № 2.6, 2.7; стр 104 №2.26.
Слайд 41
1. Сколько решений неравенства
содержится среди чисел −2, 0,1,
3?
А. 1
Б. 2
В. 3
Г. 4
К заданию 2
Закончить тест
Слайд 42
2. Сколько решений системы неравенств
содержится среди чисел
–1, 1, 2, 3?
А. 1
Б. 2
В. 3
Г. 4
К
заданию 3
Закончить тест
Слайд 43
3. Решите неравенство: х2 < 9
A. х
< 3
Б. х < ±3
В. –3< х < 3
Г.
х < –3; х > 3
К заданию 4
Закончить тест
Слайд 44
4. Решите неравенство:
A.
х < 2
Б. х > 2
В. 0 < х
< 2
Г. х < 0; х > 2
К заданию 5
Закончить тест
Слайд 45
5. Найдите натуральное значение параметра Р при котором
множество решений неравенства (1+ х)(Р – х) ≥ 0
содержит 5 целых чисел?
А. 1
Б. 2
В. 3
Г. 4
Закончить тест
К меню
Слайд 46
Верно!
Перейти к заданию 2
Перейти к заданию
3
Перейти к заданию 4
Перейти к
заданию 5
Перейти к заданию 1
Слайд 47
Посмотреть решение.
Вернуться к заданию 2
Вернуться к
заданию 1
Посмотреть решение.
Вернуться к заданию 3
Вернуться к заданию 4
Вернуться к заданию 5
Посмотреть решение.
Посмотреть решение:
Посмотреть решение.
Неверно!
Слайд 48
х
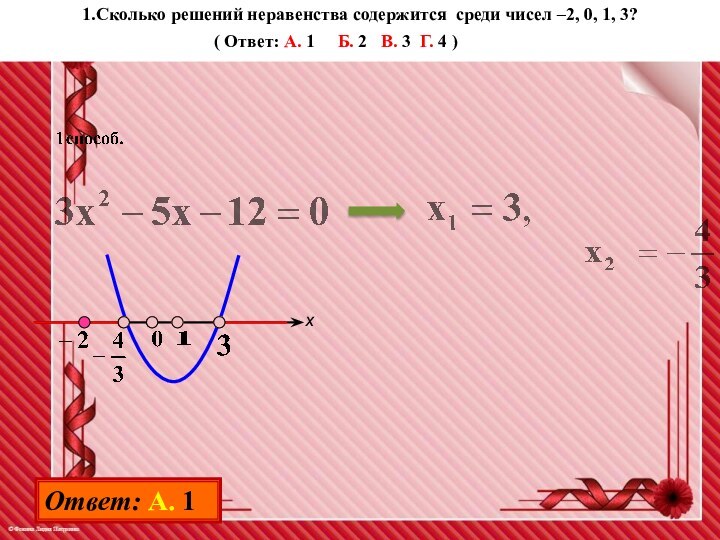
1.Сколько решений неравенства содержится среди чисел –2, 0,
1, 3?
( Ответ: А. 1 Б.
2 В. 3 Г. 4 )
Ответ: А. 1
Слайд 50
2.Сколько решений системы неравенств содержится среди чисел ---
–1, 1,
2, 3? ( Ответ: А)1, В)2, В) 3, Г) 4).
1 способ: Рассмотрим решение данной системы, подставляя значения переменной.
2 способ
Ответ: Г.
4 решения.
Слайд 51
х
2 способ
Ответ: В. −3 < x
3
3. Решите неравенство:
1 способ:
у
Слайд 52
4. Решите неравенство
1) Рассмотрим функцию
2) Рассмотрим функцию
0
1
1
х
2
Далее
Ответ:
Г. x < 0, x > 2
Слайд 53
5. Найдите натуральное значение параметра Р, при котором
множество решений неравенства (1+х)(Р – х) ≥ 0 содержит
5 целых чисел?
Ответ: А)1 Б)2 В)3 Г)4
х
-1
Р
0
1
2
3
Далее
Ответ: В. p = 3
Слайд 54
Оцените свою работу:
За 5 верно выполненных заданий- «5»
За
4 верно выполненных задания- «4»
За 3 верно выполненных задания-
«3»
Слайд 55
Перейти к заданию 2
Перейти к заданию
3
Перейти к заданию 4
Перейти к
заданию 5
Перейти к заданию 1
Закончить тест
Слайд 56
х
Далее
Ответ: В. −3 < x < 3
3. Решите неравенство:
2 способ:
+
+
─
Слайд 57
2.Сколько решений системы неравенств содержится среди чисел ---
–1, 1,
2, 3? ( Ответ: А)1, В)2, В) 3, Г) 4).
2 способ :Рассмотрим решение данной системы :
Ответ: Г.
4 решения.
+
+
─
+
+
─
B
Слайд 58
В прямоугольном параллелепипеде ABCDA1B1C1D1, у которого AB =
6, BC = 6, CC1 = 4, найдите тангенс
угла между плоскостями ACD1 и A1B1C1.
С2
4) D1О⊥ AC (ΔAD1C- равнобедренный, AD1=D1C).
Решение.
2) Вместо плоскости A1B1C1 возьмем параллельную ей плоскость ABC .
1) Построим плоскость ACD1..
3) АВСD – квадрат, диагонали АС∩BD в точке О, О – середина AC, DО⊥AC.
5) Значит, ∠D1ОD —
линейный угол искомого угла.
6) ΔD1DО – прямоугольный ⇒
Слайд 59
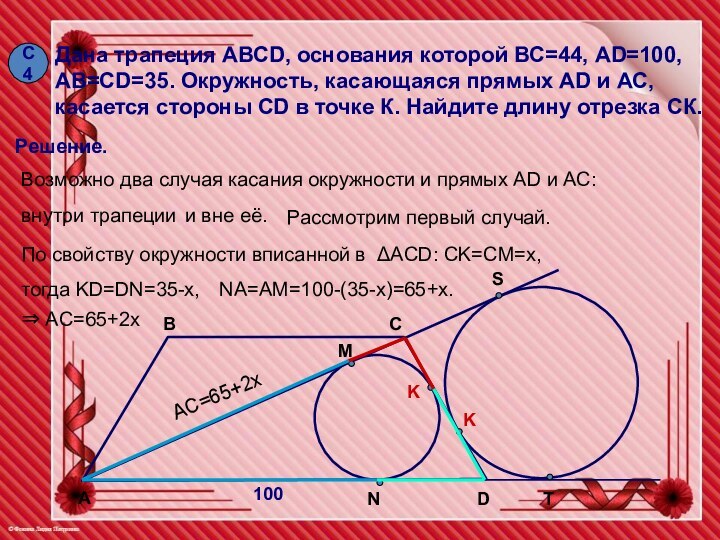
С4
Дана трапеция АВСD, основания которой ВС=44, AD=100, AB=CD=35.
Окружность, касающаяся прямых AD и АС, касается стороны CD
в точке К. Найдите длину отрезка СК.
Решение.
Возможно два случая касания окружности и прямых AD и АС:
внутри трапеции
и вне её.
Рассмотрим первый случай.
По свойству окружности вписанной в ΔACD: CK=CM=x,
тогда KD=DN=35-x,
⇒ AC=65+2x
AC=65+2x
NA=AM=100-(35-x)=65+x.
100
Слайд 60
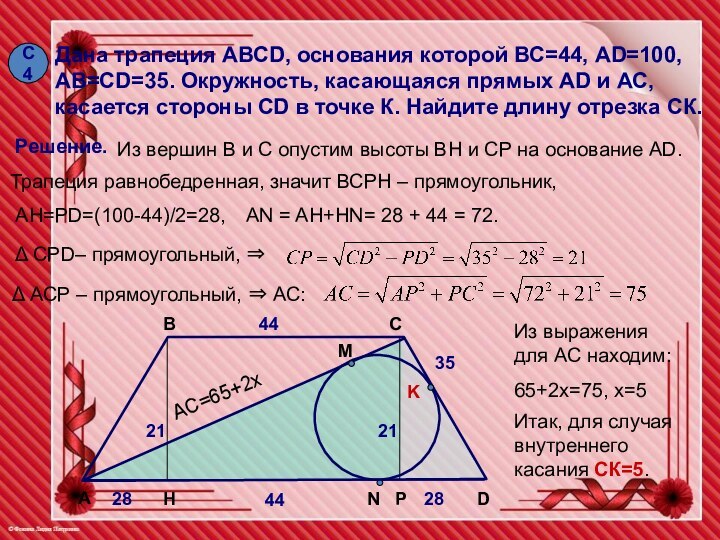
С4
Дана трапеция АВСD, основания которой ВС=44, AD=100, AB=CD=35.
Окружность, касающаяся прямых AD и АС, касается стороны CD
в точке К. Найдите длину отрезка СК.
Решение.
Н
Р
Из вершин В и С опустим высоты BH и CP на основание AD.
Δ CPD– прямоугольный, ⇒
Δ АСР – прямоугольный, ⇒ АС:
35
AH=PD=(100-44)/2=28,
Трапеция равнобедренная, значит ВСРН – прямоугольник,
AN = AH+HN= 28 + 44 = 72.
AC=65+2x
Из выражения для АС находим:
65+2х=75, х=5
Итак, для случая внутреннего касания СК=5.
Слайд 61
С4
Дана трапеция АВСD, основания которой ВС=44, AD=100, AB=CD=35.
Окружность, касающаяся прямых AD и АС, касается стороны CD
в точке К. Найдите длину отрезка СК.
Решение.
Рассмотрим второй случай.
Пусть CS=CK=x,
ТA=AS=100+(35-x)=135-x, с другой стороны,
AS=AC+CS=AC + x.
Получаем уравнение:
75 + х = 135 – х, ⇒ х = 30
Итак, во втором случае СК=30.
Ответ: 5 или 30.
тогда KD=DТ=35-x,
75
х
100
35-х
Слайд 62
А
В
С
D
K
M
T
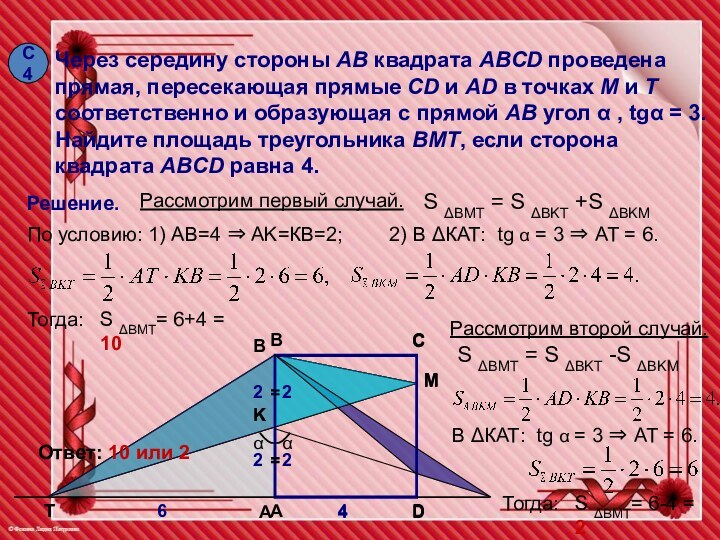
Через середину стороны AB квадрата ABCD проведена прямая,
пересекающая прямые CD и AD в точках М и
Т соответственно и образующая с прямой АВ угол α , tgα = 3. Найдите площадь треугольника ВМТ, если сторона квадрата ABCD равна 4.
Решение.
Рассмотрим первый случай.
S ΔBMT = S ΔBKT +S ΔBKM
По условию: 1) AB=4 ⇒ AK=КВ=2;
2) В ΔКАТ: tg α = 3 ⇒ АТ = 6.
α
Рассмотрим второй случай.
4
6
А
В
С
D
K
M
T
4
S ΔBMT = S ΔBKT -S ΔBKM
В ΔКАТ: tg α = 3 ⇒ АТ = 6.
α
Ответ: 10 или 2
С4
Слайд 63
Решение.
Изобразим графики левой и правой частей неравенства
х
у
-1
0
Неподвижный
«прямой угол» с вершиной в точке (-3; -1), лучи
которого направлены вверх.
.
.
-3
И сжатый в два раза «прямой угол», лучи которого направлены вверх и двигающийся вдоль оси абсцисс в зависимости от параметра а.
С5
Слайд 64
Решение.
х
у
-1
0
.
.
-3
Заметим, что неравенство не имеет решения при -4
образуют отрезок длиной 1, если расстояние между абсциссами точек
пересечения графиков равно 1.
(смотри на чертеж!)
IABI=1,и аналогично ICDI=1.
С5
Слайд 65
Решение.
х
у
-1
0
.
.
-3
Раскрывая знак модуля на каждом интервале, получим:
По условию
IАВI = 1, значит:
По условию ICDI = 1, значит:
С5
Слайд 66
Упростим каждое неравенство данной системы, выделив полный квадрат:
Решение.
x
и y
Слайд 67
Решение.
x-11
Упростим каждое неравенство данной системы,
выделив полный квадрат:
По условию ищем точки с целыми координатами,
значит достаточно проверить на принадлежность системе неравенств точки
(12;-7), (12;-8), (12;-9), (12;-10).
Проверка показывает, что условию задачи удовлетворяет единственная точка (12; -8).
Ответ: (12; -8)
B
Слайд 68
Прототипы текстовых задач на ЕГЭ и ГИА.
1.Из пункта

А в пункт В, расстояние между которыми 30 км,
одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 105 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1 час 45 минут позже автомобилиста. Ответ дайте в км/ч.
2.Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 54 км/ч, а вторую половину пути — со скоростью, на 36 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
3.В помощь садовому насосу, перекачивающему 8 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 5 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 56 литров воды?
4 .Моторная лодка прошла против течения реки 80 км и вернулась в
пункт отправления, затратив на обратный путь на 3 часа меньше.
Найдите скорость течения, если скорость лодки в неподвижной воде
равна 13 км/ч. Ответ дайте в км/ч.
Слайд 69
23 Две трубы наполняют бассейн за 3 часа

20 минут, а одна первая труба наполняет бассейн за
10 часов. За сколько часов наполняет бассейн одна вторая труба?
2 4 .В помощь садовому насосу, перекачивающему 6 литров воды за 1 минуту, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 56 литров воды?
2 5. Дима и Ваня выполняют одинаковый тест. Дима отвечает за час на 7 вопросов текста, а Ваня — на 10. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Вани на 108 минут. Сколько вопросов содержит тест?
26 Митя, Антон, Никита и Коля учредили компанию с уставным капиталом 100000 рублей. Митя внес 15% уставного капитала, Антон — 60000 рублей, Никита — 0,1 уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1100000 рублей причитается Коле? Ответ дайте в рублях.
27 .В сосуд, содержащий 8 литров 12-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составляет концентрация получившегося раствора?
B
Слайд 70
Список используемой литературы и Интернет-ресурсов
Открытый банк заданий по

математике. http://www.mathege.ru:8080/or/ege/ShowProblems?offset=0&posMask=4&showProto=true
Савченко Е.М. Оболочка для теста открытого типа
в PowerPoint. http://www.it-n.ru/communities.aspx?cat_no=16561&d_no=28752&ext=Attachment.aspx?Id=7427
Ямкина Е.В. Алгоритм создания тестов в PowerPoint. http://www.it-n.ru/communities.aspx?cat_no=6376&d_no=9854&ext=Attachment.aspx?Id=2750
http://narod.ru/disk/19724678000/221649.zip.html - ссылка на скачивание В3.
ЕГЭ 2010. Математика. Задача B3. Рабочая тетрадь. Шестаков С.А. (под ред. Семенова А.Л., Ященко И.В.)
http://www.alleng.ru/d/math/math462.htm - информация о учебном пособии В3 (книжка).
http://office.microsoft.com/ru-ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D0%B8%D0%BA&origin=FX010132103#ai:MC900434373
http://office.microsoft.com/ru-ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D0%B8%D0%BA&origin=FX010132103http://office.microsoft.com/ru-ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D0%B8%D0%BA&origin=FX010132103 http://office.microsoft.com/ru-ru/images/MC900434393.aspx
Сайт Дмитрия Гущина «РЕШУ ОГЭ» и «РЕШУ ЕГЭ».
Слайд 71
Список используемой литературы
Алгебра и начала анализа. 10-11 класс.:
Задачник для общеобразоват. учреждений / А. Г. Мордкович, Л.О.
Денищева, Т.Н. Мишустина, Е.Е. Тульчинская. – 2-е изд., испр. М.: Мнемозина, 2010.
Единый государственный экзамен: Математика: Контрол. измерит. материалы
/Л.О.Денищева, Е.М.Бойченко, Ю.А.Глазков и.др.; М-во образования Рос.
Федерации.- М.: Просвещение, 2009.
Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов / сост. Г.И.Ковалева, Т.И.Бузулина, О.Л.Безрукова, Ю.А.Розка. – Волгоград: Учитель, 2008.
Сборник задач для подготовки письменного экзамена за курс основной школы: 9-й кл. / С.А.Шестаков, И.Р.Высоцкий, Л.И.Звавич; Под ред.С.А.Шестакова. – М.: ООО «Издательство АСТ»; ООО «Издательство Астрель», 2005.