- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Тригонометрические неравенства
Содержание
- 2. Цель:Рассмотреть способы решения простейших тригонометрических неравенств.
- 3. Тригонометрические неравенстваТригонометрическиминеравенствами называютсянеравенства вида:1. sinx )а2. cos x >(((
- 4. РЕШЕНИЕ НЕРАВЕНСТВ sinx )а Построить графикифункций y= sinx и у = а, считая, что |а|
- 5. РЕШЕНИЕ НЕРАВЕНСТВ sinx )аВсегда на интервале(х0;х1) выполняетсянеравенство sinx>а,а на интервале(х1;х2) выполняетсянеравенство sinx а, где |а|
- 6. Примеры Sinx >Х0= arcsin
- 7. Решение неравенств cos x >(
- 8. Решение неравенств cos x >(а,а на интервале(х1;х2) выполняетсянеравенство cosx а, где |а|
- 9. Решение неравенств cos x >(
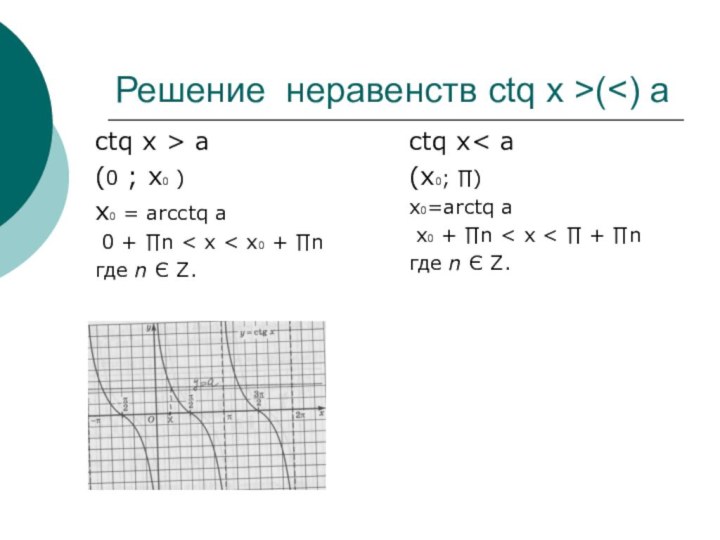
- 10. Решение неравенств tq x >( a(x0 ,
- 11. Примеры 5.tq x < 1 x0=arctq
- 12. Решение неравенств сtq x >( a(0 ;
- 13. Примеры:сtq x > 0(0 ; х0 )х0
- 14. Выполните задание:Решите неравенства и соотнесите ответы:Sin x
- 15. Правильные ответы к заданию1.
- 16. Скачать презентацию
- 17. Похожие презентации
Цель:Рассмотреть способы решения простейших тригонометрических неравенств.
Слайд 3
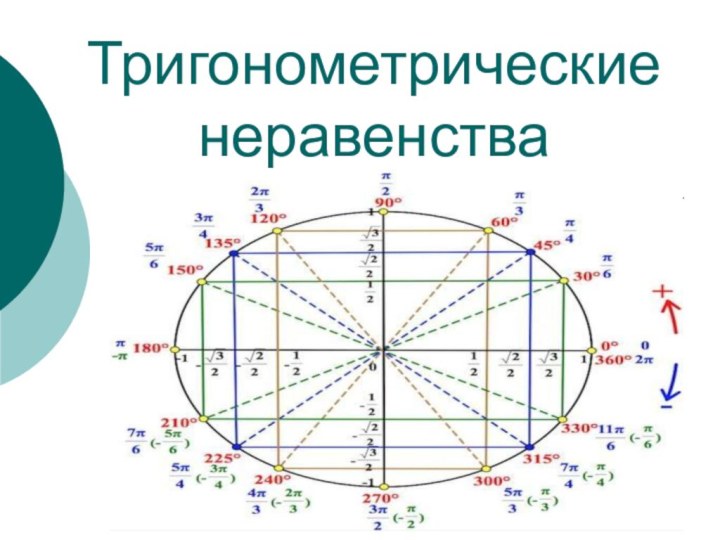
Тригонометрические неравенства
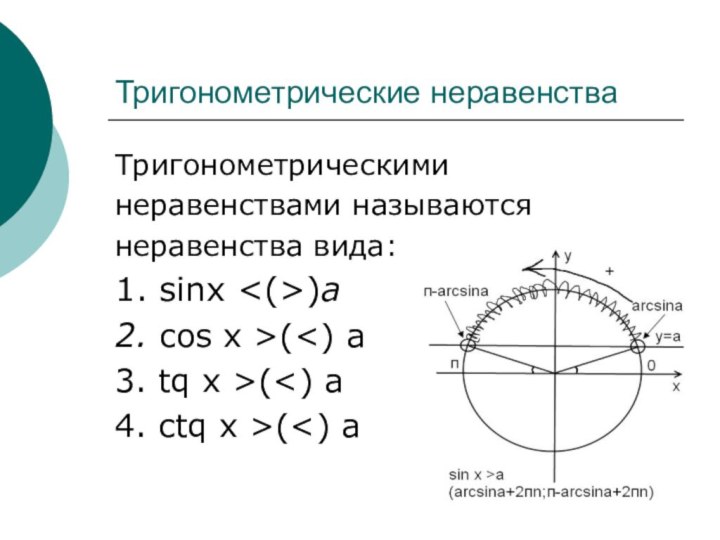
Тригонометрическими
неравенствами называются
неравенства вида:
1. sinx )а
2. cos x
Слайд 4
РЕШЕНИЕ НЕРАВЕНСТВ sinx )а
Построить графики
функций y= sinx
и
у = а, считая, что |а|
sinx = а,
х = (-1)ⁿarcsina +∏n,
где n Є Z.
Пусть n= 0,1,2,
находим три корня
составленного
уравнения
X0= arcsin a,
X1=-arcsin a+ ∏,
X2= arcsin a + 2∏.
Х0 , х1, х2 –абсциссы
трех последовательных
точек пересечения
графиков y= sinx и у=а,
Слайд 5
РЕШЕНИЕ НЕРАВЕНСТВ sinx )а
Всегда на интервале
(х0;х1) выполняется
неравенство sinx>а,
а
на интервале
(х1;х2) выполняется
неравенство sinx
синуса1. Sinx > а, где |а|<1
х0 +2∏n<х<х1 +2∏n
где n Є Z.
2. sinx<а, где |а|<1
х1 +2∏n<х<х2 +2∏n
где n Є Z.
Слайд 6
Примеры
Sinx >
Х0= arcsin =
∏
3Х1 = - arcsin + ∏=
= ∏ + ∏= 4∏
3 3
∏/3 +2∏n<х< 4∏/3+2∏n
где n Є Z.
Ответ:(∏/3 +2∏n; 4∏/3+2∏n)
2.Sinx <
Х1 = - arcsin +∏=
= ∏ + ∏= 4∏
3 3
Х2 = arcsin +2∏=
= ∏ + 2∏= 7∏
3 3
4∏/3 +2∏n<х< 7∏/3+2∏n
где n Є Z.
Ответ:
(4∏/3 +2∏n;7∏/3+2∏n)
Х0= arcsin = ∏
Х1 = - arcsin + ∏=
= ∏ + ∏= 4∏
3 3
∏/3 +2∏n<х< 4∏/3+2∏n
где n Є Z.
Ответ:(∏/3 +2∏n; 4∏/3+2∏n)
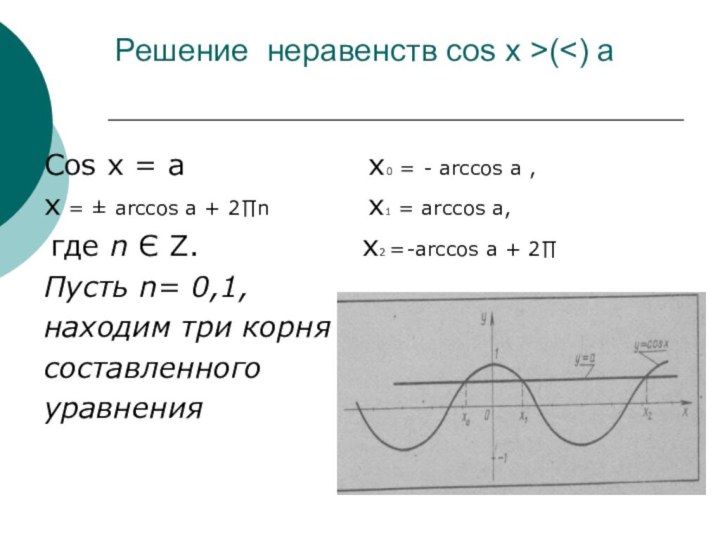
Слайд 7 Решение неравенств cos x >(
a
x0 = - arccos a ,x = ± arccos a + 2∏n x1 = arccos a,
где n Є Z. x2 =-arccos a + 2∏
Пусть n= 0,1,
находим три корня
составленного
уравнения
Слайд 8 Решение неравенств cos x >(
выполняется
неравенство cos x>а,
а на интервале
(х1;х2) выполняется
неравенство cosx
надодобавить число кратное
периоду синуса
1. Cos x > а, где |а|<1
х0 +2∏n<х<х1 +2∏n
где n Є Z.
2. Cos x < а, где |а|<1
х1 +2∏n<х<х2 +2∏n
где n Є Z.
Слайд 9 Решение неравенств cos x >(
½
x1 = arccos½ = ∏/3
x2 =-arccos½=
= - ∏/3
где
n Є Z. ∏/3+2∏n ≤ х ≤5∏/3 +2∏n
где n Є Z.
Ответ: [∏/3+2∏n, 5∏/3+2∏n]
4.Cos x ≥ ½
x0 =-arccos½ = - ∏/3
x1 = arccos½ = ∏/3
где n Є Z.
-∏/3+2∏n ≤ х ≤∏/3 +2∏n
где n Є Z.
Ответ: [-∏/3+2∏n,∏/3+2∏n]
Слайд 10 Решение неравенств tq x >(
< a
(- ∏/2 , x0 )
x0=arctq a
-∏/2 +
∏n < x < x0 + ∏n где n Є Z.
tq x > a
(x0 , ∏/2 )
x0=arctq a
x0 +∏n < x < ∏/2 + ∏n
где n Є Z.
Слайд 11
Примеры
5.tq x < 1
x0=arctq 1
= ∏/4
-∏/2 +∏n < x < ∏/4 + ∏n
где
n Є Z.Ответ:(-∏/2+∏n; ∏/4+ ∏n)
6.tq x >1
x0=arctq 1 = ∏/4
∏/4 +∏n < x < ∏/2 + ∏n
где n Є Z.
Ответ:
(∏/4 +∏n; ∏/2 + ∏n)
Слайд 12 Решение неравенств сtq x >(
a
(0 ; х0 )
х0 = arсctq a
0
+ ∏n < x < x0 + ∏n где n Є Z.
сtq x< a
(х0; ∏)
x0=arctq a
x0 + ∏n < x < ∏ + ∏n
где n Є Z.
Слайд 13
Примеры:
сtq x > 0
(0 ; х0 )
х0 =
arсctq 0 = ∏/2
0 + ∏n < x
< ∏/2 + ∏n где n Є Z.
Ответ: (∏n ; ∏/2 + ∏n),
n Є Z.
сtq x< 0
(х0; ∏)
x0=arctq 0 = ∏/2
∏/2 + ∏n < x < ∏ + ∏n
где n Є Z.
Ответ:(∏/2 + ∏n; ∏ + ∏n)
где n Є Z.
Слайд 14
Выполните задание:
Решите неравенства и соотнесите ответы:
Sin x
1
Sin x > 1
Cos x -1
Tq x
> Ctq <-
Ответы:
1. (∏+ 2∏n ; 3∏+ 2∏n)
2.(-∏+ 2∏n; ∏+ 2∏n)
3.(∏/2 + 2∏n ; ∏/2 + 2∏n)
4.(2∏/3 + ∏n ; ∏ + ∏n)
5.(∏/2 + 2∏n ; 5∏/2 + 2∏n)
6.(∏/3 + ∏n ; ∏/2 + ∏n)
