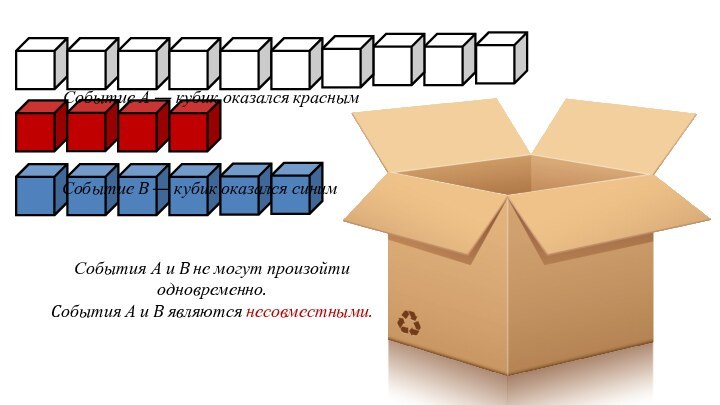
кубик оказался синим
События А и B не могут произойти
одновременно. Cобытия А и B являются несовместными.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сложение и умножение вероятностей
Содержание
- 2. Событие А — кубик оказался краснымСобытие B
- 3. Два события называют НЕСОВМЕСТНЫМИ, если в одном
- 4. ?Событие C — кубик оказался не белымСобытие
- 5. Выясним, как вероятность события С связана с
- 6. ABC
- 7. Eсли событие C означает, что наступает одно
- 8. Пример 1Есть 10 экзаменационных билетов. Ученик вытянул
- 9. Событие А — простое числоСобытие B —
- 10. Пример Свойство вероятностей противоположных событийСобытие А Выпало
- 11. Событие А Выпало 6 очков Событие B Выпало
- 12.
- 13. Пример Какова вероятность того, что сумма очков,
- 14. Рассмотрим, как можно вычислить вероятность события, состоящего
- 15. ??1824Пусть в одной из двух коробок находится
- 16. Событие А из первой коробки вынимают красный
- 17. 1824Для события С благоприятными являются те исходы, при которых оба вытянутых шара окажутся красными.
- 18. Если событие C означает совместное наступление событий
- 19. Пример. На карточках написаны числа от одного
- 20. Скачать презентацию
- 21. Похожие презентации
Событие А — кубик оказался краснымСобытие B — кубик оказался синимСобытия А и B не могут произойти одновременно. Cобытия А и B являются несовместными.
Слайд 2
Событие А — кубик оказался красным
Событие B —
кубик оказался синим
одновременно.Cобытия А и B являются несовместными.
Слайд 3
Два события называют
НЕСОВМЕСТНЫМИ,
если в одном и
том же испытании они не могут произойти одновременно, то
естьнаступление одного из них исключает наступление другого.
Слайд 4
?
Событие C — кубик оказался не белым
Событие А
— кубик оказался красным
Событие B — кубик оказался синим
Слайд 5 Выясним, как вероятность события С связана с вероятностями
каждого из событий А и B.
A
B
C
20 исходов
Благоприятных исходов:
4 6 10Слайд 7 Eсли событие C означает, что наступает одно из
двух несовместных событий А или B, то вероятность события
C равна сумме вероятностей событий А и B.
Слайд 8
Пример 1
Есть 10 экзаменационных билетов. Ученик вытянул один
из них. Какова вероятность того, что номером билета является
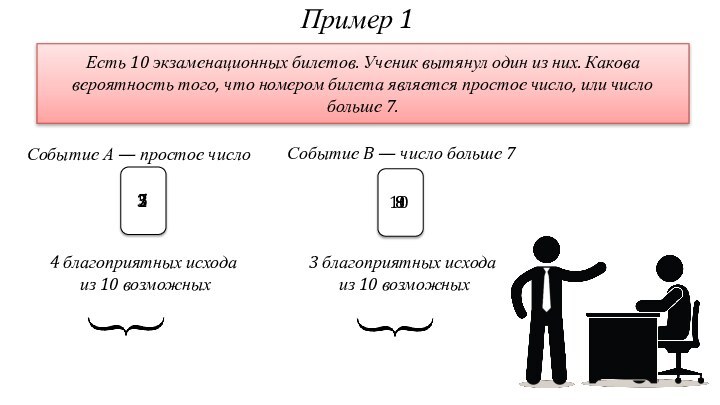
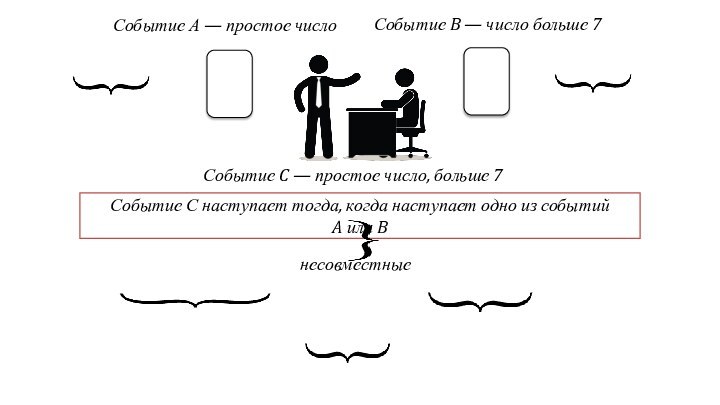
простое число, или число больше 7.Событие А — простое число
Событие B — число больше 7
4 благоприятных исхода
из 10 возможных
3 благоприятных исхода
из 10 возможных
2
3
7
5
8
9
10
Слайд 9
Событие А — простое число
Событие B — число
больше 7
Событие C — простое число, больше 7
Событие С
наступает тогда, когда наступает одно из событий A или B
несовместные
Слайд 10
Пример
Свойство вероятностей
противоположных событий
Событие А
Выпало 6
очков
Событие B
Выпало менее 6 очков
Всякое наступление события А
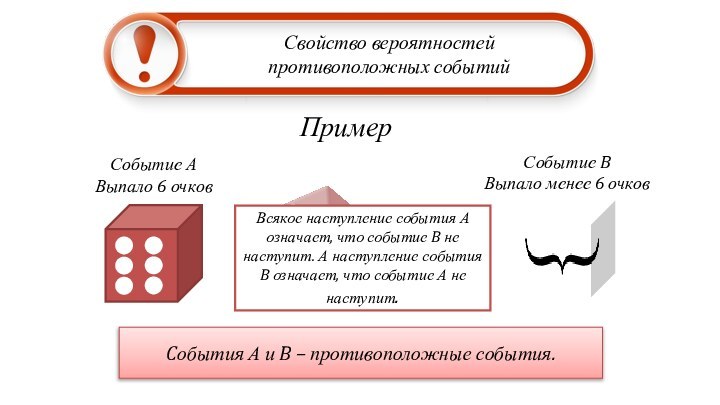
означает, что событие B не наступит. А наступление события B означает, что событие А не наступит.Cобытия А и B – противоположные события.
Слайд 11
Событие А
Выпало 6 очков
Событие B
Выпало менее
6 очков
1 благоприятный исход
из 6 возможных
5 благоприятных исходов
из 6 возможных
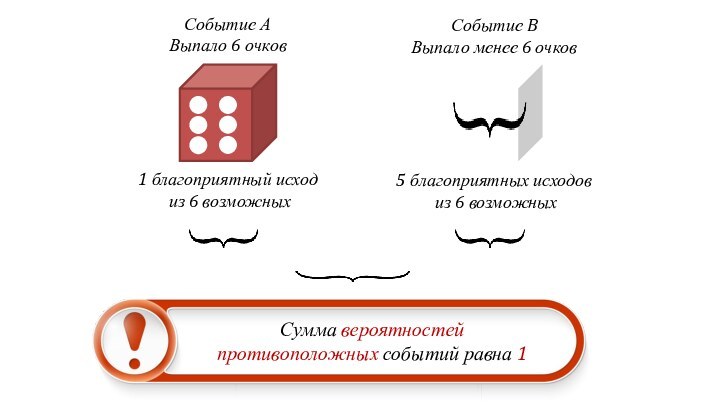
Сумма вероятностей
противоположных событий равна 1
Слайд 13
Пример
Какова вероятность того, что сумма очков, выпавших
на двух кубиках, меньше 9?
Общее число равновозможных исходов равно
36.
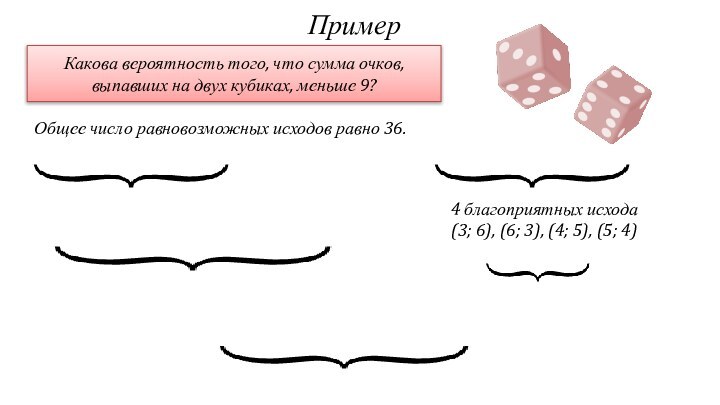
4 благоприятных исхода
(3; 6), (6; 3), (4; 5), (5; 4)
Слайд 14 Рассмотрим, как можно вычислить вероятность события, состоящего в
совместном появлении двух независимых событий.
Два события называются
НЕЗАВИСИМЫМИ,
если
наступление одного из них не влияет на вероятность наступления другого события.
Слайд 15
?
?
18
24
Пусть в одной из двух коробок находится 18
шаров, из которых 3 красные, а в другой 24
шара, из которых 4 красные. Из каждой коробки наугад вынимают по одному шару. Какова вероятность того, что оба шара окажутся красными?
Слайд 16
Событие А
из первой коробки
вынимают красный шар
Событие
B
из второй коробки
вынимают красный шар
Для события А
благоприятными являются 3 исхода из 18для события B благоприятными являются 4 исхода из 24.
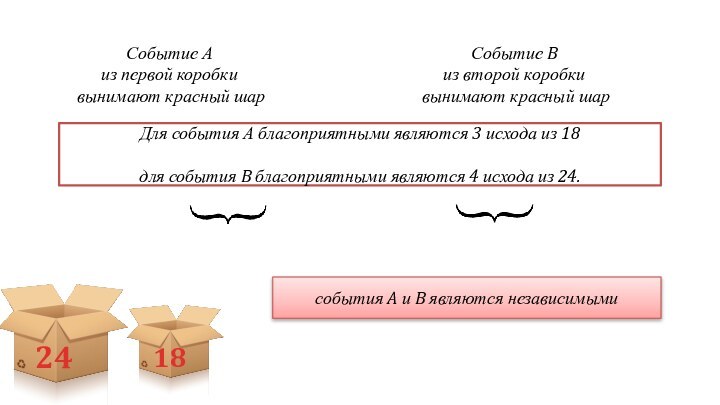
события A и B являются независимыми
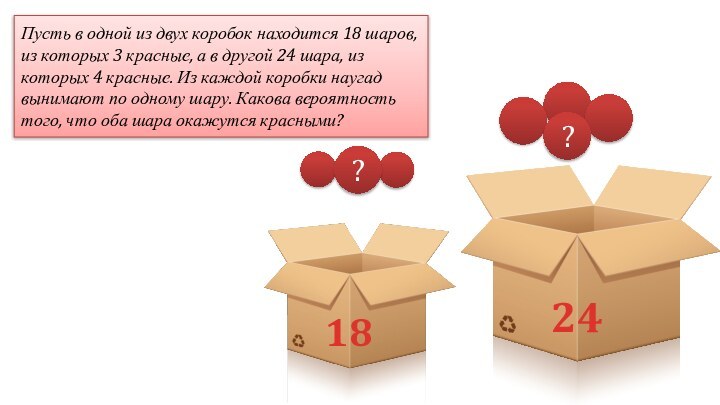
18
24
Слайд 17
18
24
Для события С благоприятными являются те исходы, при
которых оба вытянутых шара окажутся красными.
Слайд 18 Если событие C означает совместное наступление событий A
и B, то вероятность события C равна произведению вероятностей
событий А и B.
Слайд 19 Пример. На карточках написаны числа от одного до
девяти включительно. Перевернули их числами вниз и перемешали. Затем
берут наугад одну карточку, записывают ее номер и кладут обратно. Карточки снова перемешивают. Затем берут еще одну карточку и записывают ее номер. Какова вероятность того, что оба раза будут вытянуты карточки, номера которых являются простыми числами. А – событие, при котором в первый раз будет вытянута карточка с простым числом.
В – событие при котором во второй раз будет вытянута карточка с простым числом.
C – событие при котором оба раза будут вытянуты карточки с простыми числами
А и В – независимые события
