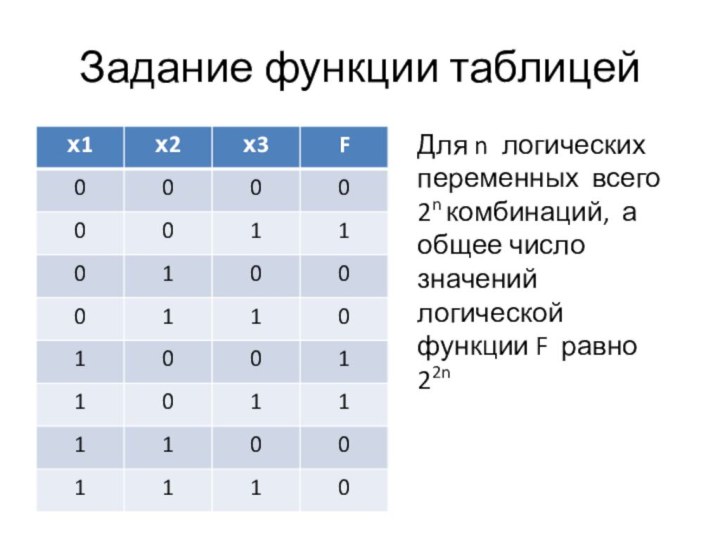
x1, x2, …, xn , принимающая значения только «истина»
или «ложь», называется логической функцией.Логические переменные и функции называются вторичными высказываниями, или молекулами.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





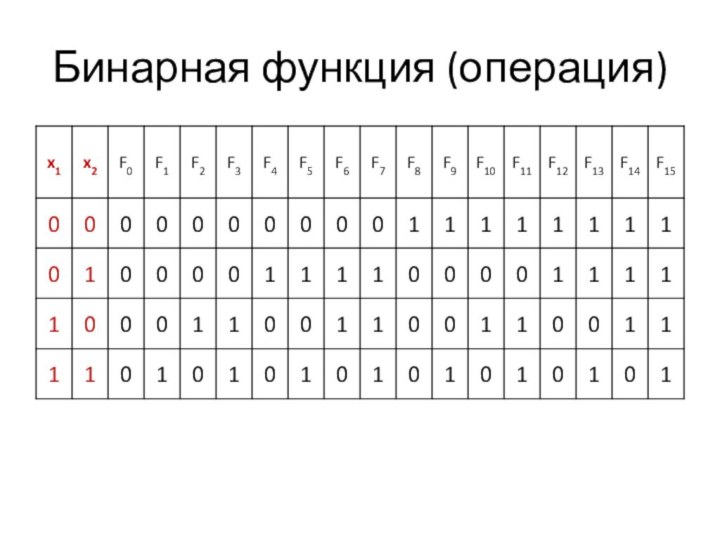







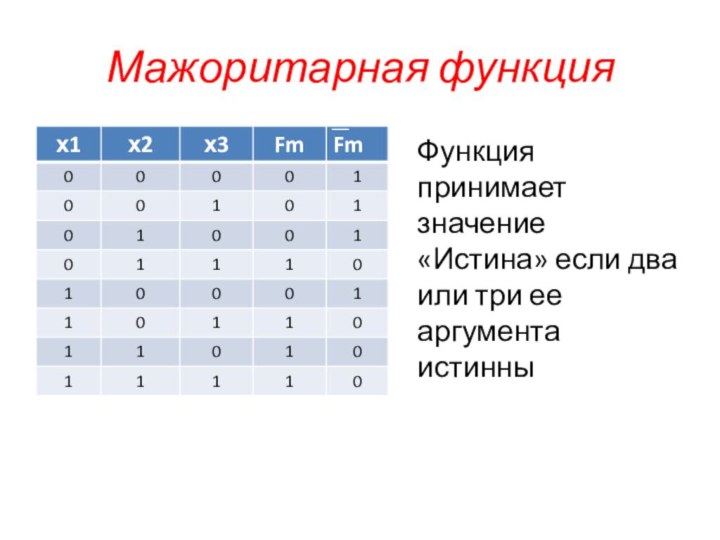

Дизъюнкция