Презентация на тему по математике Правильные многогранники

творчеству и созиданию через создание собственного образовательного продукта и

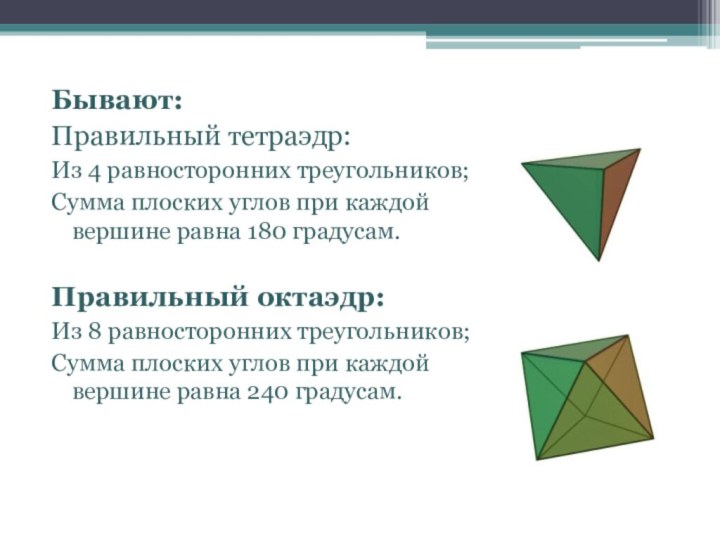
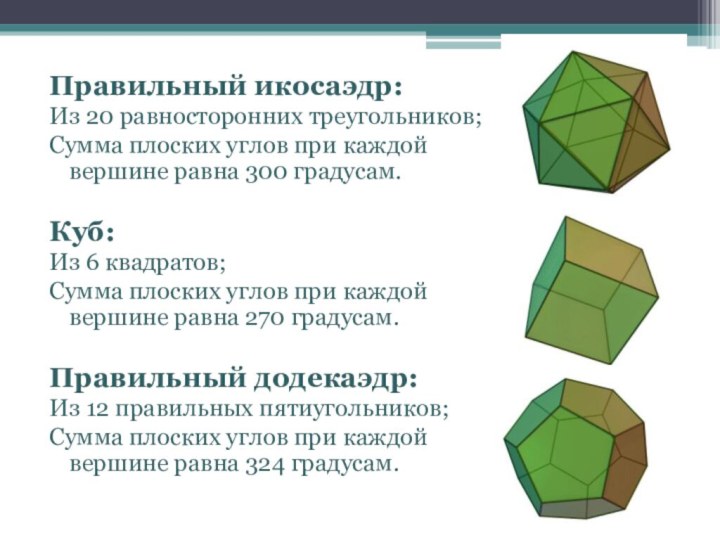
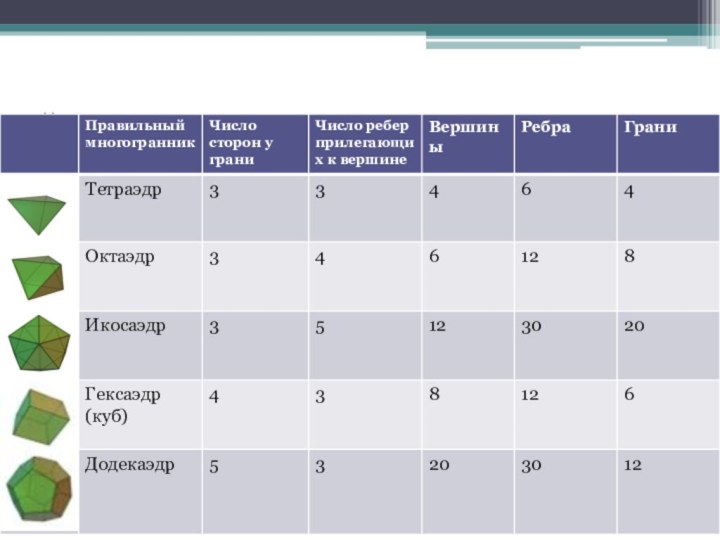
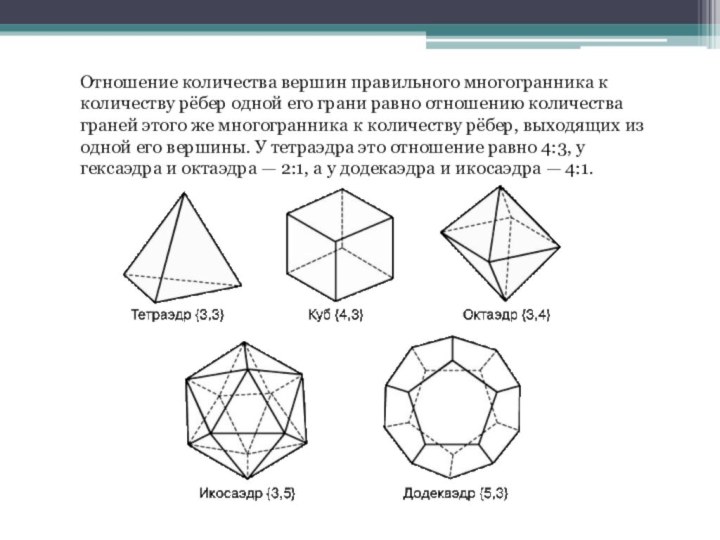
осознание его практической необходимости; развивать умения применять знания в незнакомых ситуациях.
Образовательный аспект: Сформировать понятие правильного многогранника и показать их виды.
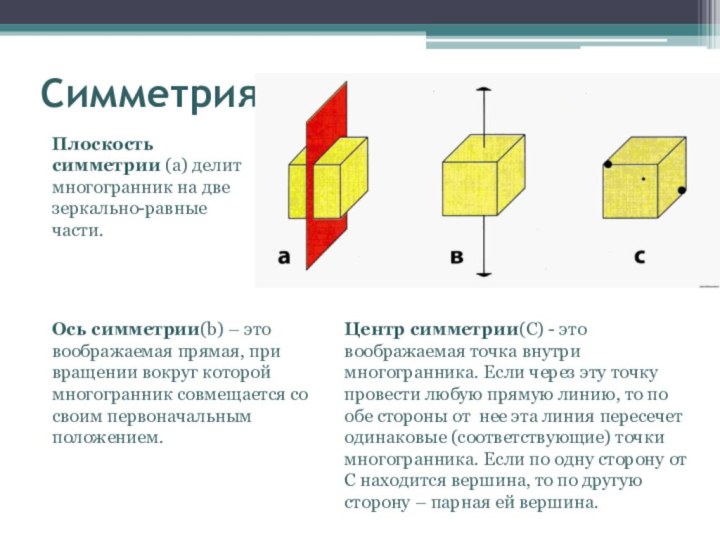
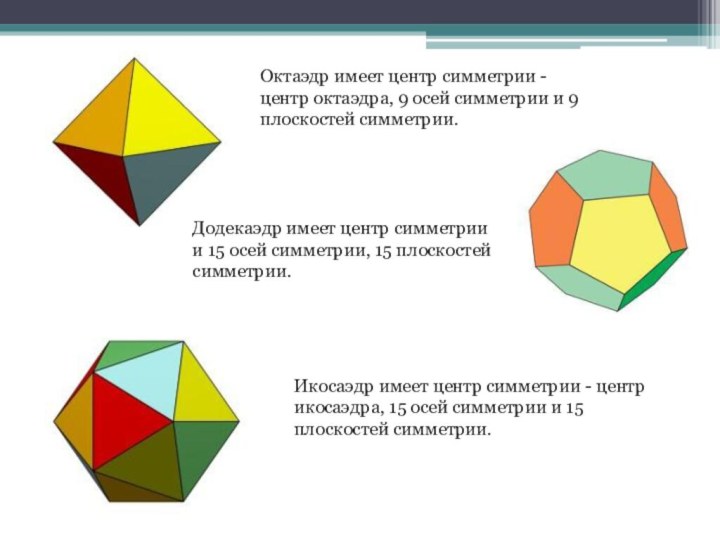
Используя понятие симметрии относительно точки, прямой, плоскости подчеркнуть общие моменты определений, рассмотреть ее исторические истоки ,основные теоретические моменты и применение .
Воспитывающий аспект: воспитывать волю и настойчивость для достижения конечных результатов при решении заданий; развивать логическое мышление учащихся; развивать чувство гармонии, прекрасного.

многоугольниками;
в каждой его вершине сходится одинаковое число рёбер.

шестиугольники, семиугольники и вообще n-угольники при n > 6.

каждой вершине равна 180 градусам.

Правильный октаэдр:
Из 8 равносторонних треугольников;
Сумма

плоских углов при каждой вершине равна 240 градусам.

каждой вершине равна 300 градусам.

Куб:
Из 6 квадратов;
Сумма плоских углов

при каждой вершине равна 270 градусам.

Правильный додекаэдр:
Из 12 правильных пятиугольников;
Сумма плоских углов при каждой вершине равна 324 градусам.

его граней и слова «грань».

симметрии(b) – это воображаемая прямая, при вращении вокруг которой

многогранник совмещается со своим первоначальным положением. 

Центр симметрии(С) - это воображаемая точка внутри многогранника. Если через эту точку провести любую прямую линию, то по обе стороны от  нее эта линия пересечет одинаковые (соответствующие) точки многогранника. Если по одну сторону от С находится вершина, то по другую сторону – парная ей вершина. 

граней (Г) и рёбер (Р) любого выпуклого многогранника простым соотношением: В

+ Г = Р + 2.

одной его грани равно отношению количества граней этого же

многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.

3 оси симметрии и 6 плоскостей симметрии.

его диагоналей.
9 осей симметрии.
9 плоскостей симметрии.

осей симметрии и 9 плоскостей симметрии.
Додекаэдр имеет центр симметрии

и 15 осей симметрии, 15 плоскостей симметрии.

Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.