- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Исследовательская работа 6 класс
Содержание
- 2. Почему минус на минус всегда только плюс.
- 3. Работу выполнила ученица 6а класса МОУ СОШ №5 г. Алагира Кучиева Кристина
- 4. «Минус на минус –
- 5. Содержание.1. Введение.2. Основная часть:
- 6. Введение. О положительных и отрицательных
- 7. "Из истории положительных и отрицательных чисел"
- 8. Давным-давно людям были известны только натуральные числа:
- 9. Отрицательные числа применяли для учета долгов или
- 10. РенеДекарт1595г -1650г.
- 11. В Европе к идее отрицательного количества достаточно
- 12. Леонардо Пизанский1170г –1250г.
- 13. Мы знаем, что
- 14. Минус на минус. -5=-1·5; -9=-1·9; -2=-1·2. То
- 15. Числа называются противоположными, если
- 16. Пусть а>0, в>0. Тогда имеем: -а·(-в)=(-а)·(-1)·в = -1·(-а)·в = -(-а)·в = а·в. Значит, Следовательно, -4·(-5)=20.-а·(-в)= а·в
- 17. s = v · t формула пути0О+-(1)(2)
- 18. Допустим мы идем вдоль дороги, нас обгоняет
- 19. 0102030м-10-20V = -10м/c Вот машина, идущая нам
- 20. Вот мы получили утверждение: (-10м/с) · (1сек)
- 21. Теперь внимание – МИНУС на МИНУС. Где
- 22. В заключении хочу сказать, что знание истории
- 23. Скачать презентацию
- 24. Похожие презентации
Почему минус на минус всегда только плюс.



















Слайд 4
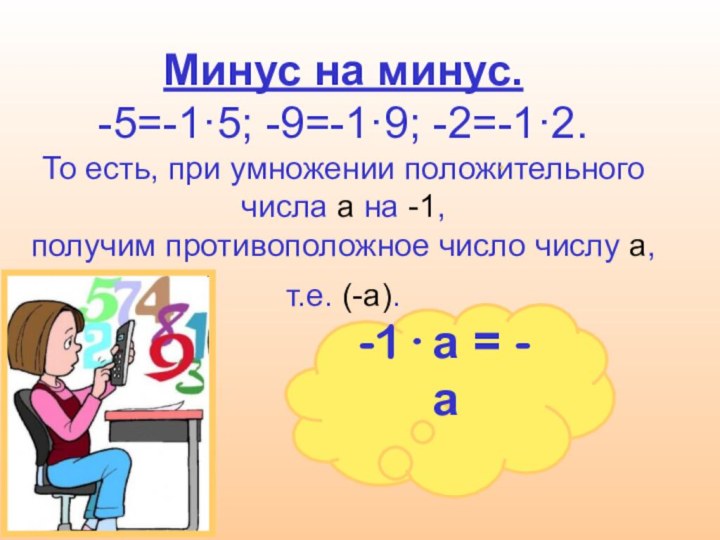
«Минус на минус –
всегда
только плюс,Отчего так бывает,
сказать не берусь».
Английский поэт - У. Г. Оден.
Слайд 5
Содержание.
1. Введение.
2. Основная часть:
а)
из истории положительных и
отрицательных чисел;б) минус на минус;
в) формула пути;
3. Заключение.
4. Литература.
Слайд 6
Введение.
О положительных и отрицательных числах
известно с глубокой древности. Больше всего ученых интересовали отрицательные
числа, которым они не «доверяли». Однако уже в наше время, мы не можем представить нашу жизнь без отрицательных чисел. Их история разнообразна, но я постараюсь рассказать вам не только об истории положительных и отрицательных чисел, но и объяснить, почему минус на минус всегда только плюс, потому что мне кажется, что если у ученика возникнут проблемы с пониманием этого материала, то дальнейшее его обучение в школе на уроках математики будут затруднительными.Слайд 8 Давным-давно людям были известны только натуральные числа: 1,2,3…
Их использовали для подсчета утвари, добычи, врагов и т.
д. Но обходиться только натуральными числами неудобно. Например, ими нельзя вычесть большее из меньшего. Для такого случая были введены отрицательные числа: китайцами – в Х в. до н. э., индийцами – в VII веке, европейцами – только в XIII веке.
Слайд 9
Отрицательные числа применяли для учета долгов или в
промежуточных вычислениях для упрощения решения уравнений. Тот факт, что
отрицательные числа в отличие от положительных не выражают наличие какой-либо сущности, вызывал сильное недоверие. Это недоверие сохранялось очень долго, и даже Декарт – один из основателей современной математики - называл их «ложными»(в ХVΙΙвеке!).
Слайд 11
В Европе к идее отрицательного количества достаточно близко
подошел в начале XIII столетия Леонардо Пизанский, однако в
явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке.Современное обозначение положительных и отрицательных чисел со знаками “ + ” и “ - ” применил немецкий математик Видман.
Слайд 13 Мы знаем, что
5 · 4 = 5 + 5 + 5 + 5 = 20 по правилу умножения, а -5 · 4 =-5+(-5)+(-5)+(-5) = -20. По переместительному закону умножения 4·(-5) = -20. А чему же равно произведение -5 · (- 4)?
Слайд 14 Минус на минус. -5=-1·5; -9=-1·9; -2=-1·2. То есть, при умножении
положительного числа а на -1, получим противоположное число числу а,
т.е. (-а).-1·а = - а
Слайд 15 Числа называются противоположными, если они отличаются
знаком. У каждого числа есть одно противоположное
число. Например, а и -а - противоположные числа. (-1)·(-а)=-(-а) =а
Слайд 16 Пусть а>0, в>0. Тогда имеем: -а·(-в)=(-а)·(-1)·в = -1·(-а)·в
= -(-а)·в = а·в.
Значит,
Следовательно, -4·(-5)=20.
-а·(-в)= а·в
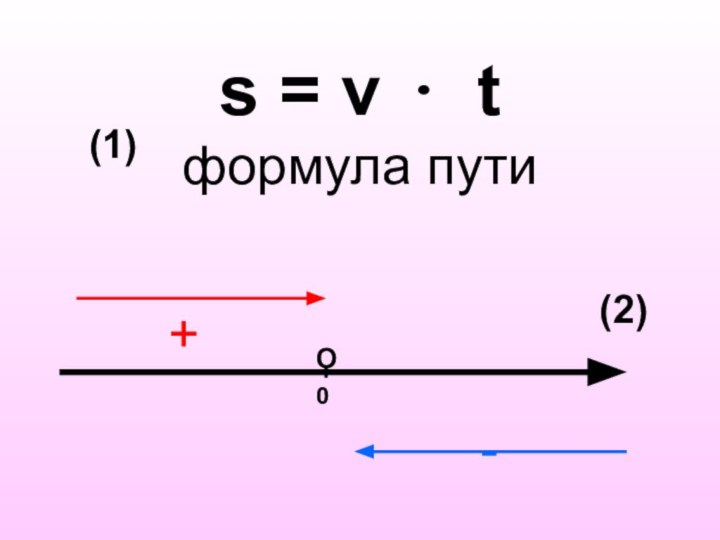
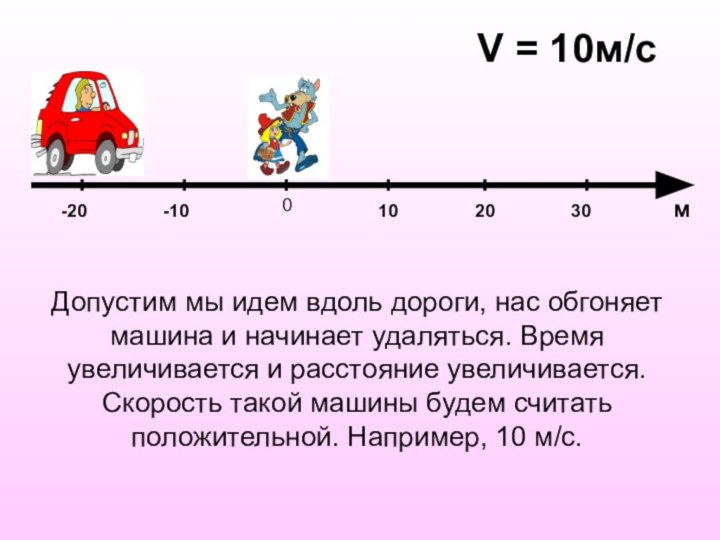
Слайд 18 Допустим мы идем вдоль дороги, нас обгоняет машина
и начинает удаляться. Время увеличивается и расстояние увеличивается. Скорость
такой машины будем считать положительной. Например, 10 м/с.0
м
10
20
30
-10
-20
V = 10м/c
Слайд 19
0
10
20
30
м
-10
-20
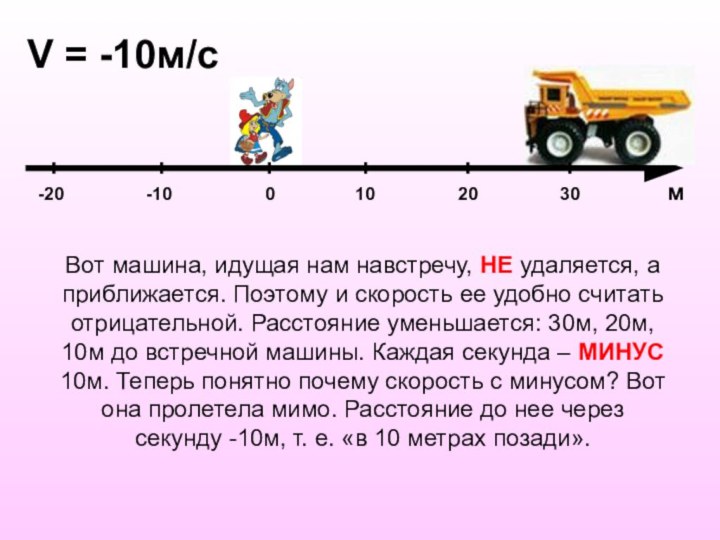
V = -10м/c
Вот машина, идущая нам навстречу,
НЕ удаляется, а приближается. Поэтому и скорость ее удобно
считать отрицательной. Расстояние уменьшается: 30м, 20м, 10м до встречной машины. Каждая секунда – МИНУС 10м. Теперь понятно почему скорость с минусом? Вот она пролетела мимо. Расстояние до нее через секунду -10м, т. е. «в 10 метрах позади».Слайд 20 Вот мы получили утверждение: (-10м/с) · (1сек) =
-10м.
(-) · (+) = (-)
отрицательная скорость
положительное время
отрицательное расстояние
(машина за спиной)Слайд 21 Теперь внимание – МИНУС на МИНУС. Где встречная
машина была за секунду ДО того, как проехала мимо?
(-10м/с) · (-1сек) = 10м.(-) · (-) = (+)
отрицательная скорость
отрицательное время
положительное расстояние (машина впереди)