Презентация на тему Графическое решение квадратных уравнений

способ
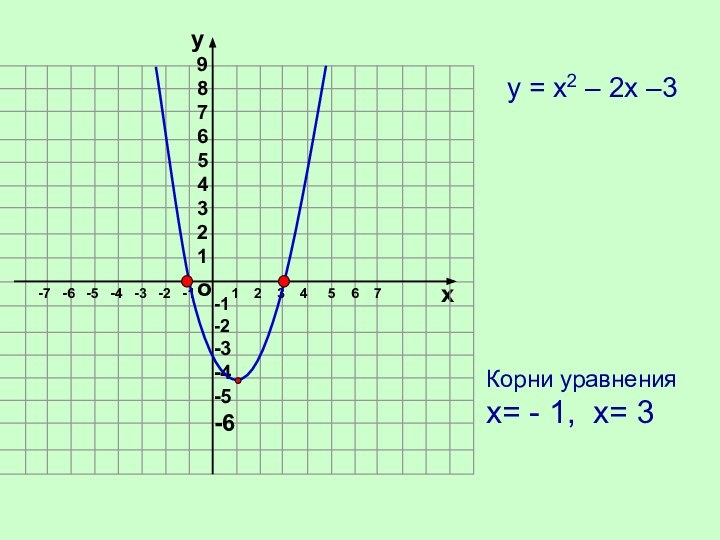
Построим график функции у = х2 – 2х –3

Найдём координаты вершины параболы:
Х0= - = 1 у0 = - 4

Значит, (1; - 4) –вершина параболы
Х = 1 ось симметрии параболы

оси параболы, например, точки х = - 1 и

х = 3. Имеем: f(- 1) = f(3) = 0.

Отметим на координатной плоскости точки (- 1; 0), (1; - 4), (3; 0) и через эти точки проведём параболу

5 6 7
-7 -6

-5 -4 -3 -2 -1

Корни уравнения
х= - 1, х= 3

у = х2 – 2х –3

+3.

Построим в одной системе координат графики
функций у = х2

и у = 2х + 3.

Графики пересекаются в двух точках А(- 1; 1) и
В(3; 9). Корнями уравнения служат абсциссы
точек А и В, т.е. х1 = - 1, х2 = 3.

5 6 7
-7

-6 -5 -4 -3 -2

Корни уравнения
х= - 1, х= 3

-1

3

у = х2
у = 2х + 3.

2х.

Построим в одной системе координат графики
Функций

у = х2 – 3 и у = 2х.

Они пересекаются в двух точках А(- 1; - 2) и
В(3; 6). Корнями уравнения являются абсциссы
точек А и В, т.е. х1 = - 1, х2 = 3.

5 6 7
-7

-6 -5 -4 -3 -2 -

Корни уравнения
х= - 1, х= 3

-1

3

у = х2 – 3
у = 2х

+ 1 - 4 = 0
и далее х2 –

2х + 1 = 4, т.е. (х - 1)2 = 4.

Построим в одной системе координат параболу
у = (х - 1)2 и прямую у = 4.

Они пересекутся в двух точках А(- 1; 4) и В(3; 4).
Корнями уравнения являются абсциссы точек
А и В, х1 = - 1, х2 = 3.

5 6 7
-7

-6 -5 -4 -3 -2

Корни уравнения
х= - 1, х= 3

3

-1

у = (х - 1)2
у = 4

получим: х – 2 – = 0;

х – 2 = .

Построим в одной системе координат гиперболу
у = и прямую у = х – 2.
Они пересекаются в двух точках А(- 1; - 3) и
В(3; 1).
Корнями уравнения являются абсциссы точек
А и В, х1 = - 1, х2 = 3.

3
-1
3
у =
у = х – 2

0
можно решить графически пятью способами.
На практике вы может

выбирать любой
понравившийся способ, но следует отметить,
что сто процентную гарантию решения
квадратного уравнения графический способ
не даёт.

= 0
(любым понравившимся способом)
Ответ: - 3; - 2