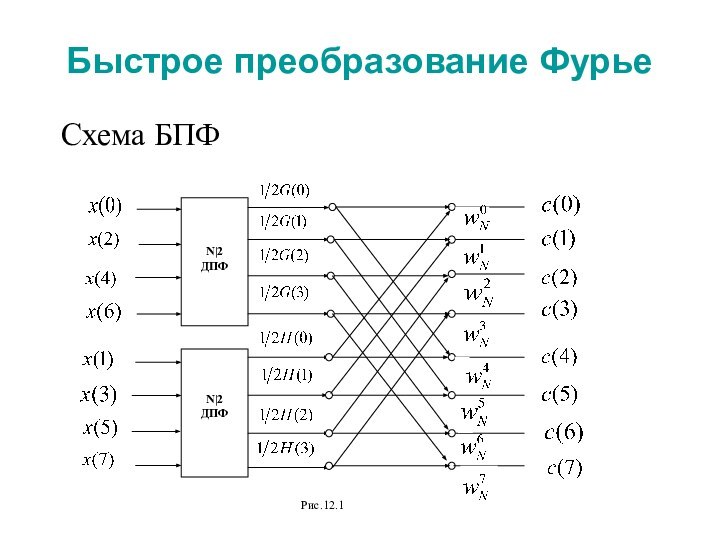
в разложении операций вычисления ДПФ сигнала длины на вычисление
преобразований Фурье с меньшим числом точек. Разделив анализируемый набор отсчетов на части, вычисляют их ДПФ и объединяют результаты. Такие процедуры получили название алгоритмов быстрого преобразования Фурье БПФ.При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени или по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).