- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Умножение вектора на число
Содержание
- 2. ЗАДАЧА№1Найдите:
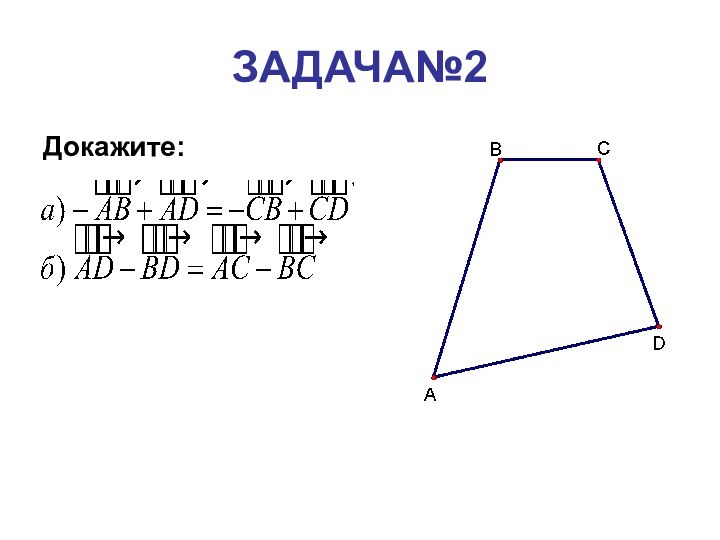
- 3. ЗАДАЧА№2Докажите:
- 4. ЗАДАЧА№3ABCD-прямоугольникAB=5; AD=12.Докажите:Найдите:
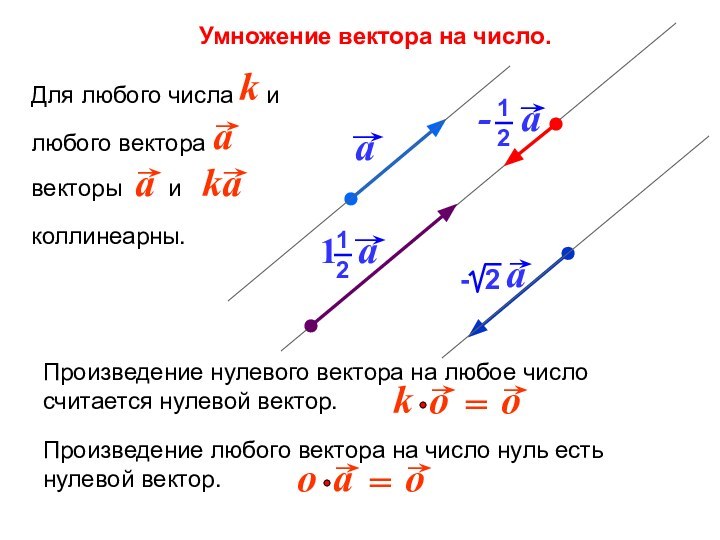
- 5. Умножение вектора на число.
- 6. Умножение вектора на число.
- 7. Умножение вектора на число.Произведение любого вектора на
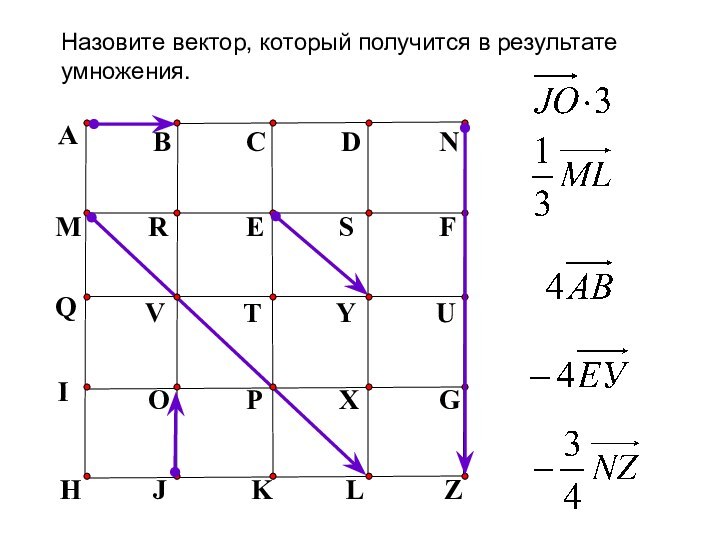
- 8. ABCDNMRESFHJKLZQVTYUНазовите вектор, который получится в результате умножения.IOPXG
- 9. х-40хABCDNMRESFHJKLZQVTYUIOPXGххххх не существует1х-1
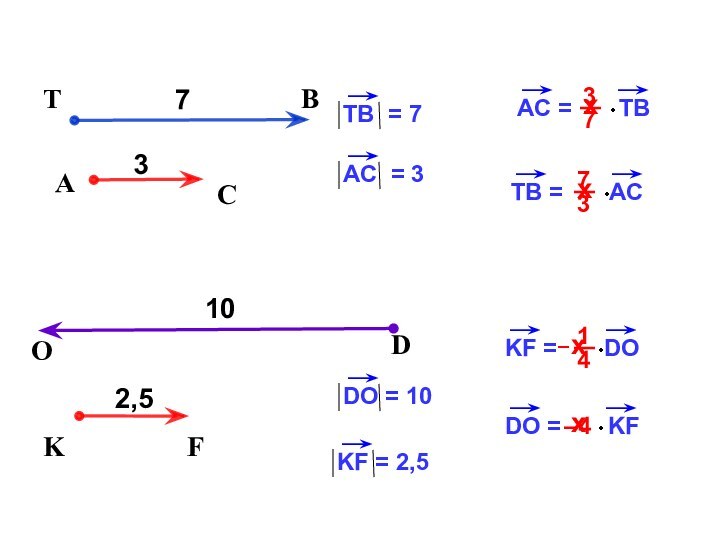
- 10. 2х3ACOKTBО – точка пересечения медиан треугольника.хх
- 11. х –4AC7TBх3хх
- 12. х1,25ACTBТВ = АСхДлина вектора TB на 25% больше длины вектора АС-0,75
- 13. BC = DA8ВСABCD – трапеция.АD10х –0,8DA = BCх
- 14. ВСABCD – параллелограмм. CS : SB
- 15. Умножение вектора на число обладает следующими основными свойствами.Сочетательный законПервый распределительный законВторой распределительный закон123
- 16. Рисунок иллюстрирует сочетательный закон. Представлен случай, когда k = 2, l = 3.Сочетательный закон1BO
- 17. BРисунок иллюстрирует первый распределительный закон. Представлен случай,
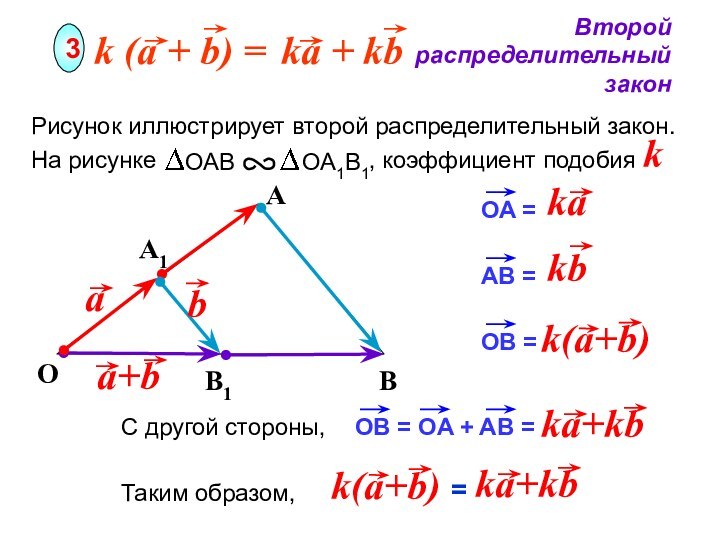
- 18. OВторой распределительный закон3AРисунок иллюстрирует второй распределительный закон.
- 19. № 781 Пусть Выразите
- 20. ЗАДАЧА №4Построить векторСАВ
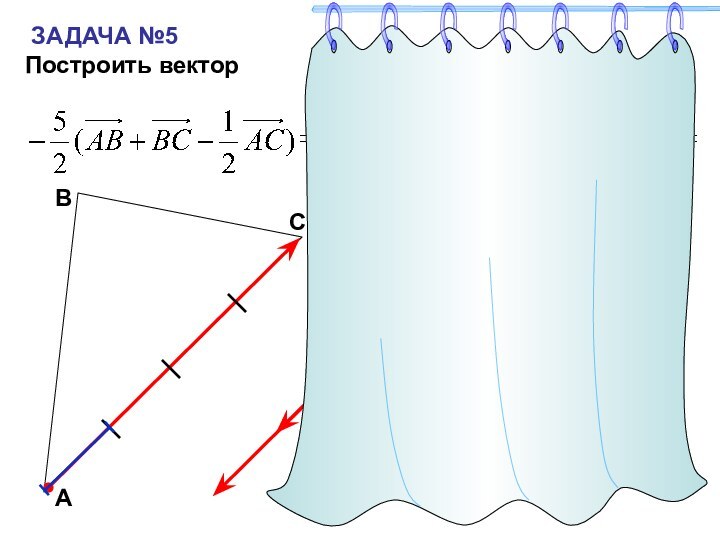
- 21. ЗАДАЧА №5Построить векторСАВ
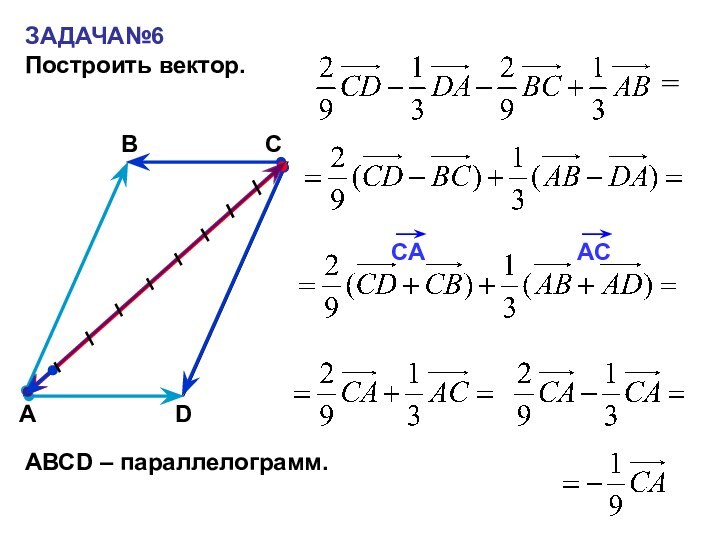
- 22. ЗАДАЧА№6Построить вектор.САВ=АВСD – параллелограмм. D
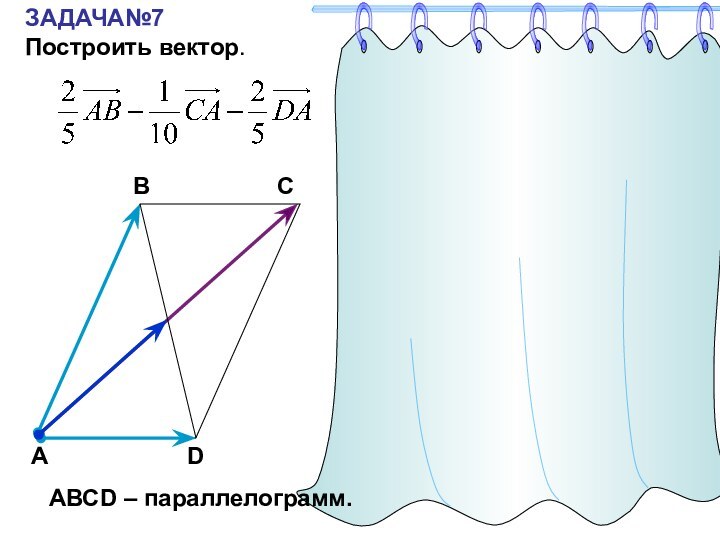
- 23. ЗАДАЧА№7Построить вектор.САВDАВСD – параллелограмм.
- 24. АВСD – ромб. Е ВС, ВЕ
- 25. Скачать презентацию
- 26. Похожие презентации
ЗАДАЧА№1Найдите:
















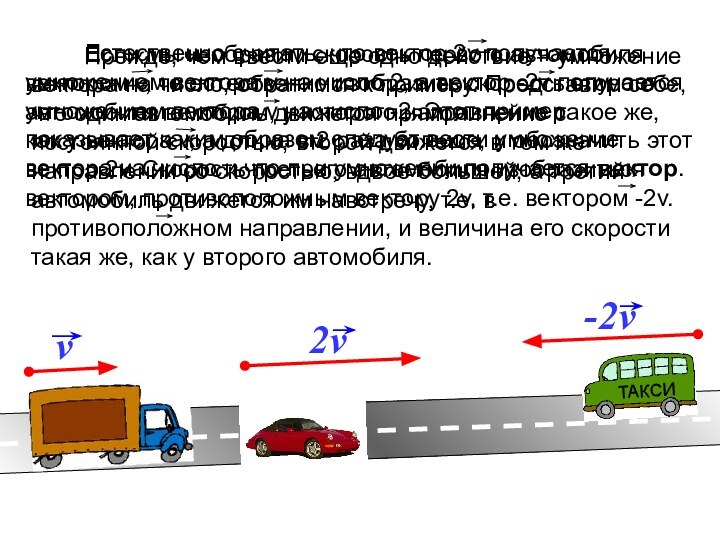
Слайд 7
Умножение вектора на число.
Произведение любого вектора на число
нуль есть нулевой вектор.
считается нулевой вектор.
Слайд 15
Умножение вектора на число обладает следующими основными свойствами.
Сочетательный
закон
Первый распределительный закон
Второй распределительный закон
1
2
3
Слайд 16 Рисунок иллюстрирует сочетательный закон. Представлен случай, когда
k = 2, l = 3.
Сочетательный закон
1
B
O
Слайд 17
B
Рисунок иллюстрирует первый распределительный закон. Представлен случай, когда
k = 3, l = 2.
O
Первый распределительный закон
2
OB
=
Слайд 18
O
Второй распределительный закон
3
A
Рисунок иллюстрирует второй распределительный закон.
На
рисунке
, коэффициент подобияk
A1
B1
B
С другой стороны,
Таким образом,
=
Слайд 24 АВСD – ромб. Е ВС, ВЕ :
ЕС = 3 : 1,
К – середина DC,
АВ = , AD = . Выразите через векторы и векторы:
С
А
В
D





























