Презентация на тему Числа Фибоначчи

Леонардо из Пизы, в современности он больше известен как

Фибоначчи.

Его отец был купцом, и Леонардо много путешествовал с ним. В путешествиях он получил те знания, которые помогли ему в дальнейшей работе.

Леонардо Пизанский
(Фибоначчи)
Около 1170 — 1250 г.

«арабской» десятичной системы счисления с ее позиционными обозначениями и

нулем.

В своем известном труде «Книга об абаке» Фибоначчи показывает превосходство десятичной системы над римской.

0 1 2 3 4 5 6 7 8 9

Арабская система счисления

Римская система счисления

Памятник Леонардо

месте, огороженном со всех сторон стеной, чтобы узнать, сколько

пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.

закономерность, которая выполняется начиная с третьего месяца:
3-й месяц –

1 + 1 = 2 пары;
4-й месяц – 1 + 2 = 3 пары;
5-й месяц – 2 + 3 = 5 пар;
6-й месяц – 3 + 5 = 8 пар и т.д.

месяцев получится ряд чисел:



1, 1, 2, 3, 5, 8,

13, 21, 34, 55, 89, 144. Ответом задачи является число 144.

Последовательность чисел получаемая в этой задаче названа в честь Леонардо: Числа Фибоначчи

площадь каждой из ее граней была равна квадрату ее

высоты.
238,7 : 147,6 = 1, 618
Наблюдения показывают, что конструкция пирамиды основана на пропорции Ф=1,618.

из них:
Найдем отношение числа ряда Фибоначчи к последующему:
Если найти

отношения числа к предыдущему, то отношение каждого числа к предыдущему стремится к Ф =1,618 (обратному к 0,618).

Отношение каждого числа к последующему более и более стремится к числу ф = 0,618 по увеличении порядкового номера.

1:1=1

1 : 2 = 0,5

2 : 3= 0,666…

3 : 5 = 0,6

5 : 8 = 0,625

8 : 13 = 0,615…

13 : 21 = 0,618

прямоугольник, у которого длина примерно в 1,6 раза больше

ширины. Другими словами стороны прямоугольника образуют так называемое золотое сечение. Слово «сечение» обозначает «деление на части». Золотое сечение отрезка – деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

если связывать золотое сечение, числа Фибоначчи и строение человеческого

тела.

Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6.

Удивительно, что последовательность чисел Фибоначчи напрямую связана со спиральность

в окружающем мире.

полого навивающихся на стержень шишки.
Хорошо видны эти же спирали

и на ананасах: обычно их бывает 8 и 13

в том, как свернулась сороконожка .

и здесь обнаружить ту же спираль, усики огурца или

свернувшийся лист также демонстрируют спиралеобразное строение.

расположение отдельных цветков. Молодые побеги папоротника, закручены в спираль

. Хорошо виден винтообразный рост веток дерева.

например таких как: смерч, ураган, облака, морские волны. Наша

галактика – это спираль.

и спирали действительно на каждом шагу окружают нас.

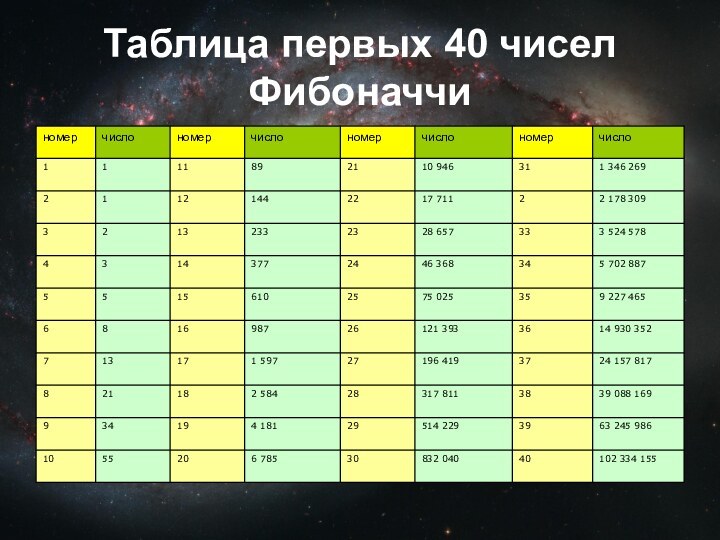
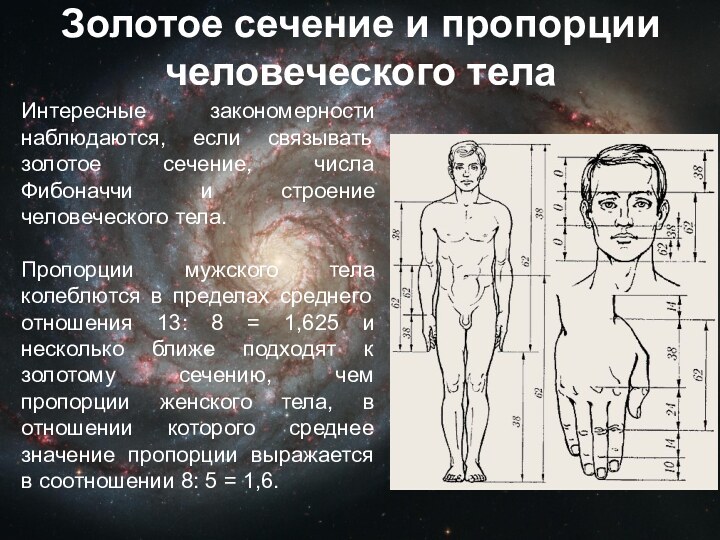
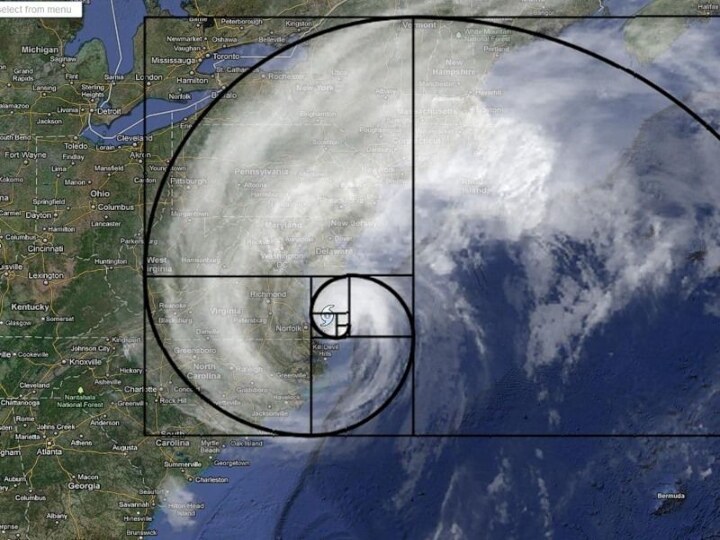
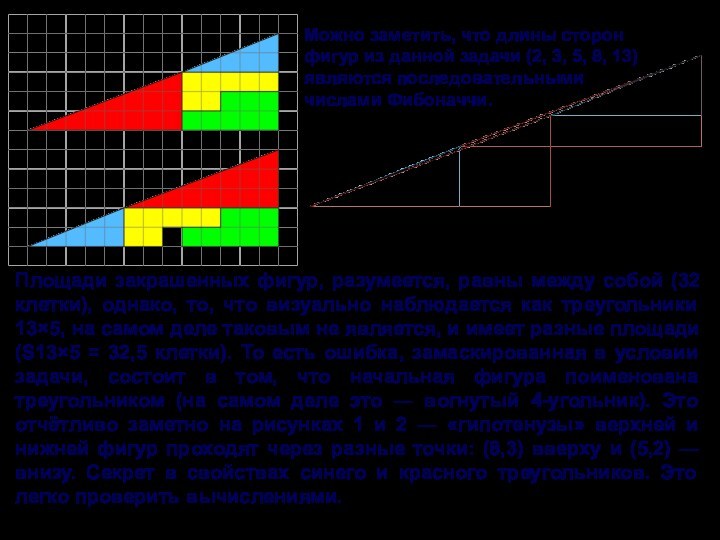
клетки), однако, то, что визуально наблюдается как треугольники 13×5,

на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунках 1 и 2 — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.

Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи.

площадью

ряда Фибоначчи равна n+2 члену без единицы.
a1 +a2+…an=an+2–1

II свойство: Сумма чисел Фибоначчи с нечётными номерами равна следующему числу с четным номером
a1+a3+a5+…+a2n-1=a2n

с чётными номерами равна следующему четному числу без единицы:
a2+

a4+a6+ …+ a2n=a2n+1-1
IV свойство: Сумма квадратов первых n чисел Фибоначчи равна произведению n-го и следующего за ним члена.
a12+ a22+a32+…+ an2= an•an+1